康托尔集(综述)
贡献者: 待更新
本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。
在数学中,康托尔集是一个位于同一直线线段上的点集,它具有许多违反直觉的性质。该集合最早由亨利·约翰·斯蒂芬·史密斯于 1874 年发现 \(^\text{[1][2][3][4]}\),并在 1883 年被德国数学家格奥尔格·康托尔提及 \(^\text{[5][6]}\)。
通过对该集合的研究,康托尔及其他数学家为现代点集拓扑奠定了基础。最常见的构造是康托尔三分集,它通过不断从一条线段中去除中间三分之一,并对剩余的每一段重复该过程来构造。康托尔在其论文中仅顺带提到了这种三分构造,作为一个 “完美但稠密度为零” 的集合的例子 \(^\text{[5]}\)。
更一般地,在拓扑学中,康托尔空间是指与康托尔三分集同胚的拓扑空间(配备其子空间拓扑)。康托尔集在自然意义上同胚于离散二点空间 \(2^\mathbb{N}\)(即离散二元集合的可数笛卡尔积)。根据 L.E.J.布劳威尔的一个定理,这等价于以下五个条件的同时满足:完美(无孤立点)、非空、紧致、可度量且零维 \(^\text{[7]}\)。
1. 三分集的构造与公式
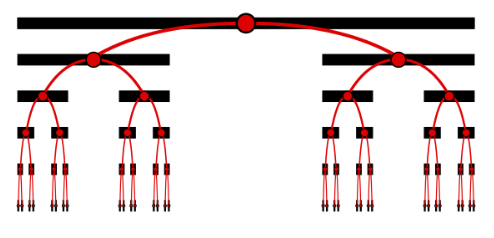
康托尔三分集(记作 $\mathcal{C}$)是通过对一组线段不断地删除中间的开放三分之一区间而构造出来的。最开始,从区间 $[0, 1]$ 中删除中间的开放三分之一区间 $\left(\frac{1}{3}, \frac{2}{3}\right)$,留下两个闭合的线段:$\left[0, \frac{1}{3}\right] \cup \left[\frac{2}{3}, 1\right]$ 接下来,对这两个剩余的线段分别删除它们的中间三分之一,得到四个线段:$\left[0, \frac{1}{9}\right] \cup \left[\frac{2}{9}, \frac{1}{3}\right] \cup \left[\frac{2}{3}, \frac{7}{9}\right] \cup \left[\frac{8}{9}, 1\right]$ 如此重复下去,康托尔三分集就是在这个无限过程中的所有步骤中都未被删除的点所组成的集合,仍然属于区间 $[0, 1]$。这个构造过程也可以用递归方式来描述。令: $$ C_0 := [0, 1]~ $$ 接着定义: $$ C_n := \frac{C_{n-1}}{3} \cup \left(\frac{2}{3} +\frac{C_{n-1}}{3}\right) = \frac{1}{3} \left(C_{n-1} \cup (2 + C_{n-1})\right) \quad \text{对所有 } n \geq 1~ $$ 于是,康托尔三分集可以表示为: $$ \mathcal{C} := \lim_{n \to \infty} C_n = \bigcap_{n=0}^{\infty} C_n = \bigcap_{n=m}^{\infty} C_n \quad \text{对任意 } m \geq 0~ $$ 这个构造过程的前六步如下图所示(原文提及有图示,此处略去)。
利用自相似变换的思想设 $T_L(x) = x/3$、$T_R(x) = (2 + x)/3$,则递归定义为:$C_n = T_L(C_{n-1}) \cup T_R(C_{n-1})$ 于是,可以写出康托尔集的显式闭式表达如下 \(^\text{[8]}\): $$ \mathcal{C} = [0, 1] \setminus \bigcup_{n=0}^{\infty} \bigcup_{k=0}^{3^n - 1} \left( \frac{3k+1}{3^{n+1}}, \frac{3k+2}{3^{n+1}} \right)~ $$ 其中每一个被移除的中间三分之一是从闭区间 $\left[ \frac{3k+0}{3^{n+1}}, \frac{3k+3}{3^{n+1}} \right] = \left[ \frac{k+0}{3^n}, \frac{k+1}{3^n} \right]$ 中去除的开区间 $\left( \frac{3k+1}{3^{n+1}}, \frac{3k+2}{3^{n+1}} \right)$。或者,康托尔集也可以表示为: $$ \mathcal{C} = \bigcap_{n=1}^{\infty} \bigcup_{k=0}^{3^{n-1}-1} \left( \left[ \frac{3k+0}{3^n}, \frac{3k+1}{3^n} \right] \cup \left[ \frac{3k+2}{3^n}, \frac{3k+3}{3^n} \right] \right)~ $$ 这里,每个闭区间 $\left[\frac{k+0}{3^{n-1}}, \frac{k+1}{3^{n-1}}\right] = \left[\frac{3k+0}{3^n}, \frac{3k+3}{3^n}\right]$ 中的中间三分之一区间 $\left(\frac{3k+1}{3^n}, \frac{3k+2}{3^n}\right)$ 通过与两端子区间 $\left[\frac{3k+0}{3^n}, \frac{3k+1}{3^n}\right] \cup \left[\frac{3k+2}{3^n}, \frac{3k+3}{3^n}\right]$ 的交集被 “移除”。
这个移除中间三分之一的过程是一个有限细分规则的简单示例。康托尔三分集的补集是分形弦的一个例子。
从算术角度来看,康托尔集由所有不需要数字 1 来表示的三进制(以 3 为底)小数组成,这些数都属于区间 $[0, 1]$。
正如上面的图示所示,康托尔集中的每一个点都可以通过一棵无限深的二叉树中的一条路径唯一确定。这条路径在每一层都会向左或向右分叉,取决于该点位于被删去线段的哪一侧。将每次向左转用 0 表示,向右转用 2 表示,便可得到该点对应的三进制小数。
曼德博对 “凝结” 式构造的描述
在《自然的分形几何》中,数学家伯努瓦·曼德博提出了一个富有想象力的思想实验,来帮助非数学读者设想集合 𝒞 的构造。他的叙述从想象一根金属棒(也许是轻质金属)开始,其中棒的物质通过迭代地向两端转移而 “凝结”。随着棒的各段变得越来越小,它们变成细长而致密的小块,最终变得太小太暗而无法看见。
凝结:康托尔棒的构造源自我称之为 “凝结” 的过程。它从一根圆柱棒开始,最好将其想象为密度极低的材料。然后,棒的物质从中间三分之一 “凝结” 到两端的三分之一部分中,使得两端部分的位置保持不变。接着,每个端三分之一的中间三分之一部分的物质再次凝结到其各自的两端三分之一部分中,如此反复无穷,直到最终剩下无限多个、无限细而密度无限高的小块。这些小块沿直线以一种由生成过程精确决定的方式分布。在这个图示中,“凝结” 最终甚至需要 “锤打” 才能继续,但当印刷机和我们的肉眼都无法再分辨时,过程便终止了:最后一行与倒数第二行已无法区分——它的每一个最终部分都被看作是一个灰色的小块,而非两个并列的黑色小块。\(^\text{[9]}\)
2. 构成
由于康托尔集是由未被排除的点构成的,因此单位区间中剩余部分的比例(即测度)可以通过计算被移除的总长度来确定。这个总长度构成一个几何级数: $$ \sum_{n=0}^{\infty} \frac{2^n}{3^{n+1}} = \frac{1}{3} + \frac{2}{9} + \frac{4}{27} + \frac{8}{81} + \cdots = \frac{1}{3} \left( \frac{1}{1 - \frac{2}{3}} \right) = 1.~ $$ 因此,剩下的比例为 $1 - 1 = 0$。
这个计算表明,康托尔集不可能包含任何非零长度的区间。也许令人惊讶的是,竟然还有东西剩下——毕竟,被移除区间的总长度正好等于原始区间的长度。然而,仔细观察这个构造过程可以发现,必定有东西被保留下来,因为每次移除 “中间三分之一” 实际上是移除开区间(即不包含端点的集合)。比如,从原始区间 $[0, 1]$ 中移除线段 $(\frac{1}{3}, \frac{2}{3})$,实际上保留了端点 $\frac{1}{3}$ 和 $\frac{2}{3}$。后续的每一步也不会移除这些端点或其他端点,因为每次被移除的区间始终是当前保留区间的内部部分。因此,康托尔集并非空集,而且实际上包含不可数无限多个点(这可由前文中关于无穷二叉树路径的描述推得)。
看起来好像只剩下了构造过程中那些被保留下来的端点,但实际上并非如此。例如,数 $\frac{1}{4}$ 有唯一的三进制形式 $0.020202\ldots = 0.\overline{02}$。它处于最底部的三分之一,再处于该部分上方三分之一的部分,再处于那部分的底部三分之一,如此反复。由于它从未出现在任何一个中间三分之一段中,因此它从未被移除。但它也不是任何中间段的端点,因为它不是 $1/3$ 的任何幂的整数倍。\(^\text{[10]}\)
所有这些被移除区间的端点都是终止的三进制小数,并且属于集合: $$ \left\{ x \in [0,1] \mid \exists i \in \mathbb{N}_0: x \cdot 3^i \in \mathbb{Z} \right\} \quad \left( \subset \mathbb{N}_0 \cdot 3^{-\mathbb{N}_0} \right)~ $$ 这是一个可数无限的集合。而就基数而言,康托尔集中的绝大多数元素既不是端点,也不是像 $1/4$ 这样的有理数点。整个康托尔集事实上是不可数的。
3. 性质
基数
可以证明,在康托尔集的构造过程中,最终保留下来的点与最初一样多,因此康托尔集是不可数的。为说明这一点,我们展示一个函数 $f$ 从康托尔集 $\mathcal{C}$ 映射到闭区间 $[0,1]$,使得 $f$ 是满射(即 $f$ 将 $\mathcal{C}$ 映射到整个 $[0,1]$),从而说明 $\mathcal{C}$ 的基数不少于 $[0,1]$ 的基数。由于 $\mathcal{C} \subseteq [0,1]$,其基数也不会更大,因此根据康托–伯恩施坦–施罗德定理,两者的基数实际上是相等的。
为构造这个函数,我们考虑 $[0,1]$ 区间内的点在三进制(base 3)表示中的形式。回想一下,某些三进制小数,特别是集合 $\left( \mathbb{Z} \setminus \{0\} \right) \cdot 3^{-\mathbb{N}_0}$ 中的元素,存在不止一种表示方法。例如:$\frac{1}{3}$ 可以写作 $0.13 = 0.1\overline{0}_3$,也可以写作 $0.0222\ldots_3 = 0.0\overline{2}_3$;$\frac{2}{3}$ 可以写作 $0.2_3 = 0.2\overline{0}_3$,也可以写作 $0.1222\ldots_3 = 0.1\overline{2}_3$。\(^\text{[11]}\) 在构造康托尔集的第一步中,被移除的是所有三进制形式为 $0.1xxxxx\ldots_3$ 的数字,其中 $xxxxx\ldots_3$ 是介于 $00000\ldots_3$ 与 $22222\ldots_3$ 之间的任意数字序列。因此,第一步之后剩下的数字形式为:
- 形如 $0.0xxxxx\ldots_3$ 的数(包括 $0.022222\ldots_3 = 1/3$);
- 形如 $0.2xxxxx\ldots_3$ 的数(包括 $0.222222\ldots_3 = 1$)。
简而言之,第一步后留下的点就是那些三进制表示中小数点后第一位不是 1 的数。值得强调的是,像 1、$\frac{1}{3} = 0.13$ 和 $\frac{7}{9} = 0.213$ 这样的数属于康托尔集,因为它们的三进制表示完全由 0 和 2 组成:$1 = 0.222\ldots_3 = 0.\overline{2}_3,\frac{1}{3} = 0.0222\ldots_3 = 0.0\overline{2}_3 ,\frac{7}{9} = 0.20222\ldots_3 = 0.20\overline{2}_3 $。所有上述数字都是 “端点”,并且这些例子是康托尔集 $\mathcal{C}$ 的右极限点。康托尔集的左极限点也存在类似情况,例如 $\frac{2}{3} = 0.1222\ldots_3 = 0.1\overline{2}_3 = 0.2\overline{0}_3,\frac{8}{9} = 0.21222\ldots_3 = 0.21\overline{2}_3 = 0.22\overline{0}_3$。所有这些端点都是正规三进制分数(即属于集合 $\mathbb{Z} \cdot 3^{-\mathbb{N}_0}$ 的元素),形式为 $p/q$,其中当该分数为最简形式时,分母 $q$ 是 3 的幂。\(^\text{[10]}\) 这些分数的三进制表示要么是终止的(即有限的),要么——如前所述,正规三进制分数通常有两种表示方式——是无限的,并 “以” 无限重复的 0 或无限重复的 2 结尾。如果一个这样的分数的三进制表示中不包含数字 1,且 “以” 无限重复的 0 结尾,那么它是康托尔集 $\mathcal{C}$ 的左极限点。类似地,如果一个正规三进制分数的表示中同样不含 1,但 “以” 无限重复的 2 结尾,那么它就是 $\mathcal{C}$ 的右极限点。
这个端点集合在康托尔集 $\mathcal{C}$ 中是稠密的(但在区间 $[0,1]$ 中不是稠密的),并且构成一个可数无限集。康托尔集中那些不是端点的数,它们的三进制表示也仅包含 0 和 2,但不能以无限重复的 0 或 2 结尾,否则它们就会是端点了。
从康托尔集 $\mathcal{C}$ 到区间 $[0,1]$ 的函数是这样定义的:取三进制表示中只包含 0 和 2 的数字,将其中所有的 2 替换为 1,然后将所得的序列解释为一个实数的二进制表示。用公式表示为:
$$
f\left(\sum_{k \in \mathbb{N}} a_k \cdot 3^{-k} \right) = \sum_{k \in \mathbb{N}} \frac{a_k}{2} \cdot 2^{-k}~
$$
其中
$$
\forall k \in \mathbb{N} : a_k \in \{0, 2\}.~
$$
对于区间 $[0,1]$ 中的任意一个数 $y$,可以通过将其二进制表示中的所有 1 替换为 2,转换为某个属于康托尔集 $\mathcal{C}$ 的数 $x$ 的三进制表示。通过这种方式,有 $f(x) = y$,因此 $y$ 是函数 $f$ 的值域中的一个值。例如,若 $y = \frac{3}{5} = 0.100110011001\ldots_2 = 0.\overline{1001}$ 则 $x = 0.\overline{2002}= 0.200220022002\ldots_3 = \frac{7}{10}$ 从而 $f$ 是一个满射函数。然而,$f$ 并非单射。函数 $f(x)$ 会在某些不同的 $x$ 上取相同的值,这些 $x$ 恰好位于被移除的某一个中间三分段的两端。例如:
$\frac{1}{3} = 0.0\overline{2}_3$,它是康托尔集的右极限点,也是中间三分段 $[ \frac{1}{3}, \frac{2}{3} ]$ 的左端点;
$\frac{2}{3} = 0.2\overline{0}_3$,它是康托尔集的左极限点,也是该中间段的右端点。
于是有: $$ \begin{array}{lcl} f\left( \frac{1}{3} \right) &=& f(0.0\overline{2}_3) = 0.0\overline{1}_2 = 0.1_2 = 0.1\overline{0}_2 \\ &=& f(0.2\overline{0}_3) = f\left( \frac{2}{3} \right) \\ &\parallel \\ &\frac{1}{2} \end{array}~ $$ 因此,康托尔集中的点的数量与区间 $[0, 1]$ 中的点一样多,其不可数基数为 $\mathfrak{c} = 2^{\aleph_0}$(即实数集的基数)。然而,被移除区间的端点集合是可数的,因此在康托尔集中必然存在不可数多个不是区间端点的点。如上文所述,其中一个例子是 $\frac{1}{4}$,其三进制表示为 $0.020202\ldots_3 = 0.\overline{02}$。事实上,对于任意 $a \in [-1, 1]$ 都存在 $x, y \in \mathcal{C}$ 使得 $a = y - x$。这一点最早由斯坦豪斯(Steinhaus)于 1917 年通过几何方法证明,他证明了一个等价命题:$\left\{(x, y) \in \mathbb{R}^2 \mid y = x + a \right\} \cap (\mathcal{C} \times \mathcal{C}) \neq \emptyset\quad \text{对任意 } a \in [-1, 1]$\(^\text{[12]}\) 也就是说,在平面上任意一条斜率为 1、截距为 $a$ 的直线,总能与 $\mathcal{C} \times \mathcal{C}$ 相交。由于这个构造从区间 $[-1, 1]$ 到 $\mathcal{C} \times \mathcal{C}$ 提供了一个单射,因此我们有:$|\mathcal{C} \times \mathcal{C}| \geq |[-1, 1]| = \mathfrak{c}$ 作为直接推论。如果我们接受对任意无限集合 $A$ 都有 $|A \times A| = |A|$(这是塔尔斯基证明等价于选择公理的一个命题),那么这就提供了另一种证明康托尔集的基数为 $|\mathcal{C}| = \mathfrak{c}$ 的方式。
康托尔集中的点数量与其取自的区间一样多,然而它本身不包含任何非零长度的区间。无理数集也具有这一性质,但康托尔集还有一个额外性质:它是闭集,因此在任何区间中都不是稠密的,这与无理数不同——无理数在每个区间中都是稠密的。
有一个猜想认为:所有代数无理数都是正规数。而康托尔集中的元素在三进制下都不是正规数,因此这一猜想将意味着:康托尔集中的所有数要么是有理数,要么是超越数。
自相似性
康托尔集是分形的原型。它是自相似的,因为它等于两个自身的拷贝,这两个拷贝分别缩小了 1/3 倍并进行了平移。更确切地说,康托尔集等于它的两个自相似变换——左变换和右变换——的并集,其中:左变换为 $T_L(x) = x/3$,右变换为 $T_R(x) = (2 + x)/3$。这两个变换在同胚意义下保持康托尔集的不变性,即: $$ T_L(\mathcal{C}) \cong T_R(\mathcal{C}) \cong \mathcal{C} = T_L(\mathcal{C}) \cup T_R(\mathcal{C})~ $$ 对 $T_L$ 和 $T_R$ 反复迭代可以形象地表示为一棵无限二叉树。在这棵树的每个节点上,可以选择左子树或右子树。将变换集 $\{T_L, T_R\}$ 与函数复合操作一起考虑,会形成一个二元幺半群。
这棵二叉树的自同构是它的双曲旋转,由模群给出。因此,在某种意义上,康托尔集是一个齐性空间,即对于康托尔集 $\mathcal{C}$ 中的任意两点 $x$ 和 $y$,都存在一个同胚映射 $h: \mathcal{C} \to \mathcal{C}$ 使得:$h(x) = y$ 若将康托尔集看作是可数多个离散空间 $\{0,1\}$ 的积空间,则可以更容易地描述这种 $h$ 的显式构造。例如,定义一个映射:$h: \{0,1\}^{\mathbb{N}} \to \{0,1\}^{\mathbb{N}}$ 令:$h_n(u) := u_n + x_n + y_n \mod 2$ 这个映射 $h$ 是一个对合同胚,它将点 $x$ 和 $y$ 互换。
拓扑与分析性质
尽管人们通常所说的 “康托尔集” 特指上述的中间三分之一构造的原始康托尔集,但在拓扑学中,常常会提到 “一个康托尔集”,指的是与原始康托尔集同胚(即在拓扑意义上等价)的任意拓扑空间。
如前述级数计算所示,康托尔集是不可数的,但其勒贝格测度为 0。由于康托尔集是开集并的补集,它本身是实数集中的一个闭子集,因此是一个完备度量空间。此外,康托尔集还是全有界的,根据海涅–博雷尔定理,它必须是紧致的。
对于康托尔集中的任意一点及其任意小的邻域,总能找到其他:三进制表示仅含 0 和 2 的点;以及三进制表示中包含 1 的点。
因此,康托尔集中的每一点都是它自身的聚点(也称为极限点或集积点),但没有一点是其内点。在拓扑学中,一个闭集若其每一点都是聚点,则称为完美集;而一个区间中的闭子集若无内点,则称为该区间中稠密处处不在的集合。
此外,康托尔集中的每个点也是其补集的聚点。
对于康托尔集中的任意两点,它们在某一位三进制数字上必然不同——一个是 0,另一个是 2。根据这一位的数值,可以将康托尔集划分为两个 “半集”,从而把这两点分隔开。这种划分将康托尔集划分成两个闭集,并将原来的两点隔离开来。在康托尔集的相对拓扑中,这样的划分是由一个既开又闭的集合完成的。因此,康托尔集是全不连通的。作为一个紧致的、全不连通的豪斯多夫空间,康托尔集是一个斯通空间的例子。
作为一个拓扑空间,康托尔集天然地与可数多个离散拓扑空间 $\{0,1\}$ 的积空间同胚。这个空间可以表示为所有二进制序列的集合: $$ 2^{\mathbb{N}} = \{(x_n) \mid x_n \in \{0,1\},\ n \in \mathbb{N} \}~ $$ 这个集合也可以与 2-进制整数等同。在积拓扑中,开集的基是所谓的柱状集合;而这个同胚映射将柱状集合对应到康托尔集从实数自然拓扑中继承的子空间拓扑。
将康托尔空间描述为紧空间的乘积,借助提霍诺夫定理,提供了康托尔空间为紧空间的第二种证明。
根据上述构造方式,康托尔集在拓扑意义上与 p-进制整数同胚,而若从中去掉一个点,则它与 p-进制数同胚。
康托尔集是实数集的一个子集,而实数是一个带有普通距离度量的度量空间;因此,康托尔集本身在使用相同度量的前提下也是一个度量空间。或者,也可以在集合 $2^{\mathbb{N}}$ 上使用 p-进制度量:对于两个序列 $(x_n),\ (y_n) \in 2^{\mathbb{N}}$,它们之间的距离定义为:$d((x_n), (y_n)) = 2^{-k}$ 其中 $k$ 是满足 $x_k \ne y_k$ 的最小索引;如果不存在这样的 $k$,说明两个序列完全相同,此时距离定义为 0。这两种度量在康托尔集上生成相同的拓扑结构。
如上文所述,康托尔集是一个全不连通、完美、紧致的度量空间。事实上,从某种意义上说,它是唯一的:任何非空的、全不连通的、完美的、紧致度量空间都与康托尔集同胚。关于与康托尔集同胚的空间,详见 “康托尔空间”。
康托尔集有时被视为紧致度量空间范畴中的 “泛对象”,因为任意紧致度量空间都可以看作是康托尔集的连续映像;然而这种映射并不是唯一的,因此严格意义上,康托尔集并不构成一个范畴论中的真正 “泛对象”。这个 “泛性” 性质在泛函分析中有重要应用,有时被称为紧致度量空间的表征定理。\(^\text{[13]}\)
对于任意整数 $q \geq 2$,群 $G = \mathbf{Z}_q^{\omega}$(即可数个 $\mathbf{Z}_q$ 的直和)上的拓扑是离散的。尽管庞特里亚金对偶群 $\Gamma$ 也是 $\mathbf{Z}_q^{\omega}$,但 $\Gamma$ 的拓扑是紧致的。可以证明 $\Gamma$ 是全不连通且完美的,因此它与康托尔集同胚。当 $q = 2$ 时,最容易写出这个同胚映射的显式形式。(参见 Rudin 1962,第 40 页。)
测度与概率
康托尔集可以看作是二进制序列构成的紧群,因此它自然携带有一个 Haar 测度。当这个测度被归一化为使整个康托尔集的测度为 1 时,它就可以看作是无限次掷硬币序列的模型。
此外,可以证明:单位区间上的勒贝格测度是康托尔集上的 Haar 测度的一个像(image),而康托尔集自然嵌入到三进制区间的方式,则是一个典型的奇异测度的例子。还可以证明,Haar 测度可以被看作是任意概率测度的一个像,从这个意义上说,康托尔集在某些方面是一个泛概率空间。
在勒贝格测度理论中,康托尔集是一个例子:它是不可数的,但测度为零的集合。\(^\text{[14]}\) 相比之下,在 Hausdorff 测度下,康托尔集在其本身的维度 $\log 2 / \log 3$ 中具有测度为 1。\(^\text{[15]}\)
康托尔数
如果我们将 “康托尔数” 定义为康托尔集中的一个成员,那么有以下结论:\(^\text{[16]}\)
- 区间 $[0, 2]$ 中的每一个实数都可以表示为两个康托尔数的和;
- 任意两个康托尔数之间总存在一个不属于康托尔集的数。
描述性集合论
作为 $[0,1]$ 的子集,康托尔集是一个稀疏集,也称为第一类集合;但作为其自身的子集时则不是,因为康托尔集是一个 Baire 空间。因此,康托尔集展示了这样一个事实:关于集合 “大小” 的不同概念——基数、测度和(Baire)范畴——并不总是一致的。与集合 $\mathbb{Q} \cap [0,1]$ 类似,康托尔集 $\mathcal{C}$ 在某些意义上是 “小” 的:它是一个零测度集,同时也是 $[0,1]$ 中的稀疏子集。但与 $\mathbb{Q} \cap [0,1]$ 不同的是,后者是可数的,其基数为 $\aleph_0$,而康托尔集的基数与 $[0,1]$ 相同,即连续统基数 $\mathfrak{c}$,在基数意义上是 “大的”。事实上,我们还可以构造出以下两种子集:一个在 $[0,1]$ 中是稀疏集但具有正测度;一个在 $[0,1]$ 中非稀疏但测度为零。具体构造如下:\(^\text{[17]}\) 取一列 “胖康托尔集” $\mathcal{C}^{(n)}$,它们的测度为 $\lambda= n - 1/n$(参见下文中的史密斯–沃尔特拉–康托尔集的构造),那么集合 $\mathcal{A} := \bigcup_{n=1}^{\infty} \mathcal{C}^{(n)}$ 的测度为正(恰为 1),但它在 $[0,1]$ 中仍是稀疏的,因为每个 $\mathcal{C}^{(n)}$ 都是处处稀疏的。再考虑集合:$\mathcal{A}^c := [0,1] \setminus \bigcup_{n=1}^{\infty} \mathcal{C}^{(n)}$ 由于 $\mathcal{A} \cup \mathcal{A}^c = [0,1]$ 且 $\mu(\mathcal{A}) = 1$,说明补集 $\mathcal{A}^c$ 不能是稀疏的,但它的测度必须为零。
4. 变体
史密斯–沃尔特拉–康托尔集
在康托尔集的构造中,我们每次都移除每段的中间三分之一。但我们也可以选择移除任意固定百分比(除了 0% 和 100%)的中间部分。比如,在每次迭代中移除区间中间的 $\frac{8}{10}$,会得到一个非常直观的例子:该集合由 $[0, 1]$ 中所有十进制表示仅包含 0 和 9 的数字组成。如果每一步都移除一个固定比例的中间部分,那么最终剩余集合的总长度趋于零,因为 $(1 - f)^n \to 0 \quad \text{当 } n \to \infty$ 对于任意 $0 < f \leq 1$,因此极限集合的勒贝格测度为零。
另一方面,也可以通过在每一步移除较小比例的中间部分,构造出具有正测度的 “胖康托尔集”。因此,可以构造出与康托尔集同胚、但仍具有正勒贝格测度且处处稀疏的集合。如果在第 $n$ 步从每段中移除长度为 $r^n$ 的区间(其中 $r \leq 1/3$),那么总共被移除的长度为:$\sum_{n=1}^{\infty} 2^{n-1} r^n = r/(1 - 2r)$ 因此,最终剩下的集合的勒贝格测度为:$\lambda =(1 - 3r)/(1 - 2r)$ 从这个意义上看,中间三分之一康托尔集是一个极限情形,对应 $r = 1/3$。如果 $0 < r < 1/3$,则剩余部分的测度满足:$0 < \lambda < 1$ 其中 $r = 1/4$ 的情形被称为史密斯–沃尔特拉–康托尔集,它的勒贝格测度为:$1/2$
康托尔尘
康托尔尘是康托尔集的多维版本。它可以通过将康托尔集与自身进行有限次笛卡尔积来构造,从而形成一个康托尔空间。与康托尔集类似,康托尔尘的勒贝格测度为零。\(^\text{[19]}\)
康托尔集的另一种二维类似物是谢尔宾斯基地毯。该构造方法是将一个正方形分成九个较小的正方形,并移除中间的一个。然后对剩下的每个正方形再次进行相同的操作:分成九个小方块并移除中间的那个,如此无限进行。\(^\text{[20]}\) 其三维类似物之一是孟格海绵。
5. 历史备注
康托尔引入了我们今天称为康托尔三分集 $\mathcal{C}$,作为一个例子:“一个完美点集,但在任意小的区间内都不处处稠密。”\(^\text{[21][22]}\) 他用三进制展开来描述 $\mathcal{C}$,称其为:“所有满足以下公式的实数组成的集合:$z = c_1/3 + c_2/3^2 + \cdots + c_\nu/3^\nu + \cdots$ 其中系数 $c_\nu$ 任意取 0 或 2,这个级数可以是有限项或无限项。”\(^\text{[21]}\)
在拓扑学中,一个拓扑空间 $P$ 是完美的,如果它的所有点都是极限点,或者等价地,如果它等于它的导集 $P'$。像 $\mathcal{C}$ 这样的实数子集可以在诱导的子空间拓扑下看作拓扑空间。\(^\text{[7]}\)
康托尔是由于对三角级数唯一性问题的研究而被引导到对导集的研究的。\(^\text{[22]}\) 这一研究在他发展抽象的、一般的无限集理论方面起到了重要作用。伯努瓦·曼德博写了大量关于康托尔尘、它们与自然分形及统计物理之间关系的著作。\(^\text{[9]}\) 他还反思了这类结构在数学界和物理学界中引发的困惑甚至反感。在《自然的分形几何》中,他写道:“我在 1962 年开始研究这个主题时,大家一致认为康托尔尘至少和科赫曲线、皮亚诺曲线一样怪异。” 并补充道:“任何有自尊的物理学家一听到康托尔的名字就会自动敬而远之,恨不得离主张 $\mathcal{C}$ 在科学中有意义的人远远躲开。”\(^\text{[9]}\)
6. 另见
- 康托尔集的指示函数
- 史密斯–沃尔特拉–康托尔集
- 康托尔函数
- 康托尔立方体
- 安托万项链
- 科赫雪花
- 克纳斯特–库拉托夫斯基扇形
- 按豪斯多夫维数分类的分形列表
- 莫泽–德布鲁因数列
7. 注释
- 史密斯,亨利·J.S.(1874 年):《关于不连续函数的积分》,载于《伦敦数学会会刊》(第一系列),第 6 卷,第 140–153 页。
- “康托尔集” 也由保罗·杜·布瓦–雷蒙(Paul du Bois-Reymond,1831–1889)发现。参见:du Bois-Reymond, Paul(1880),《积分计算基本定理的证明》(德文原文为 “Der Beweis des Fundamentalsatzes der Integralrechnung”),发表于《数学年刊》Mathematische Annalen,第 16 卷,第 128 页脚注。
- “康托尔集” 还于 1881 年被维托·沃尔特拉(Vito Volterra,1860–1940)发现。参见:Volterra, Vito(1881),《关于逐点不连续函数的一些观察》(意大利文原文为 “Alcune osservazioni sulle funzioni punteggiate discontinue”),载于《数学杂志》Giornale di Matematiche,第 19 卷,第 76–86 页。
- 费雷罗斯,何塞(1999):《思想的迷宫:集合论的历史及其在现代数学中的作用》,瑞士巴塞尔:Birkhäuser 出版社,第 162–165 页,ISBN 9783034850513。
- 伊恩·斯图尔特(Ian Stewart)(1997 年 6 月 26 日):《上帝掷骰子吗?:混沌的新数学》,企鹅出版社,ISBN 0140256024。康托尔,格奥尔格(1883):《关于无限线性点丛 V》(德文原文:“Über unendliche, lineare Punktmannigfaltigkeiten V”),发表于《数学年刊》Mathematische Annalen,第 21 卷,第 545–591 页,DOI: [10.1007/bf01446819](https://doi.org/10.1007/bf01446819),S2CID: 121930608。原文存档于 2015 年 9 月 24 日,检索于 2011 年 1 月 10 日。
- 皮特根(H.-O. Peitgen)、于尔根斯(H. Jürgens)、绍普(D. Saupe)(2004):《混沌与分形:科学的新前沿》(第 2 版),纽约:施普林格出版社,第 65 页,ISBN 978-1-4684-9396-2。
- 凯赫里斯,亚历山大·S(Alexander S. Kechris)(1995):《经典描述性集合论》(Classical Descriptive Set Theory),《数学研究生教材》系列第 156 卷,纽约施普林格出版社,第 31、35 页,DOI: [10.1007/978-1-4612-4190-4](https://doi.org/10.1007/978-1-4612-4190-4),ISBN 978-0-387-94374-9。
- 索尔塔尼法尔,穆森(Mohsen Soltanifar)(2006):《对一类中间-a 康托尔集的不同描述》,发表于《美国本科生研究期刊》American Journal of Undergraduate Research,第 5 卷第 2 期,第 9–12 页,DOI: [10.33697/ajur.2006.014](https://doi.org/10.33697/ajur.2006.014)。
- 曼德博,伯努瓦·B(Benoit B. Mandelbrot)(1983):《自然的分形几何》(更新增订版),纽约,ISBN 0-7167-1186-9,OCLC 36720923。
- Belcastro, Sarah-Marie;Green, Michael(2001 年 1 月):“康托尔集中包含 $\frac{1}{4}$?真的吗?”,载于《大学数学期刊》(The College Mathematics Journal),第 32 卷第 1 期,第 55 页,DOI: [10.2307/2687224](https://doi.org/10.2307/2687224),JSTOR: 2687224。
- 数值具有终止表示时,其另一种循环表示形式在**具有阿基米德绝对值**的任意进位制系统中都会出现。
- Carothers, N. L.(2000):《实分析》(Real Analysis),剑桥大学出版社,第 31–32 页,ISBN 978-0-521-69624-1。
- Willard, Stephen(1968):《一般拓扑》(General Topology),Addison-Wesley 出版社,ASIN B0000EG7Q0。
- Irvine, Laura:“定理 36:康托尔集是一个不可数但测度为零的集合”,载于《本周定理》(Theorem of the Week),原文档案保存于 2016 年 3 月 15 日,检索日期:2012 年 9 月 27 日。
- Falconer, K. J.(1986 年 7 月 24 日):《分形集合的几何》(The Geometry of Fractal Sets),剑桥大学出版社,第 14–15 页,ISBN 9780521337052。PDF 版。
- Schroeder, Manfred(1991):《分形、混沌、幂律:来自无限天堂的片段》(Fractals, Chaos, Power Laws: Minutes from an Infinite Paradise),Dover 出版社,第 164–165 页,ISBN 0486472043。
- Gelbaum, Bernard R.(1964):《分析中的反例》(Counterexamples in Analysis),与 Olmsted, John M. H.(John Meigs Hubbell,1911–1997)合著,旧金山:Holden-Day 出版社,ISBN 0486428753,OCLC 527671。
- “径向康托尔集”(Radial Cantor Set)。
- Helmberg, Gilbert(2007):《认识分形》(Getting Acquainted With Fractals),Walter de Gruyter 出版社,第 46 页,ISBN 978-3-11-019092-2。
- Helmberg, Gilbert(2007):《认识分形》(Getting Acquainted With Fractals),Walter de Gruyter 出版社,第 48 页,ISBN 978-3-11-019092-2。
- 康托尔,格奥尔格(2021):《集合论通论基础:对无限理论的数理-哲学探讨》("Foundations of a general theory of sets: A mathematical-philosophical investigation into the theory of the infinite",James R. Meyer 英文翻译),[www.jamesrmeyer.com,第 10 节脚注 22,检索时间:2022 年 5 月 16 日。](http://www.jamesrmeyer.com,第 10 节脚注 22,检索时间:2022 年 5 月 16 日。)
- Fleron, Julian F.(1994):《关于康托尔集与康托尔函数历史的一则注释》,载于《数学杂志》(Mathematics Magazine),第 67 卷第 2 期,第 136–140 页,DOI: [10.2307/2690689](https://doi.org/10.2307/2690689),ISSN 0025-570X,JSTOR: 2690689。
8. 参考文献
- Steen, Lynn Arthur;Seebach, J. Arthur Jr.(1995 年)[原始版本 1978 年]:《拓扑中的反例》(Counterexamples in Topology),Dover 对 1978 年版的再版,柏林、纽约:Springer-Verlag,第 29 个例子,ISBN 978-0-486-68735-3,MR 0507446。
- Wise, Gary L.;Hall, Eric B.(1993 年):《概率与实分析中的反例》(Counterexamples in Probability and Real Analysis),纽约:牛津大学出版社,第 1 章,ISBN 0-19-507068-2。
- Falconer, K. J.(1986 年 7 月 24 日):《分形集合的几何》(Geometry of Fractal Sets),剑桥数学丛书,剑桥大学出版社,ISBN 0521337054。
- Mattila, Pertti(1999 年 2 月 25 日):《欧几里得空间中集合与测度的几何:分形与可整化性》(Geometry of Sets and Measures in Euclidean Space: Fractals and Rectifiability),剑桥高级数学研究系列,剑桥大学出版社,ISBN 0521655951。
- Mattila, Pertti(2015 年):《傅里叶分析与豪斯多夫维数》(Fourier Analysis and Hausdorff Dimension),剑桥高级数学研究系列,剑桥大学出版社,ISBN 9781316227619。
- Zygmund, A.(1958 年):《三角级数》(Trigonometric Series),第一卷与第二卷,剑桥大学出版社。
9. 外部链接
- “康托尔集”,《数学百科全书》,EMS Press,2001 年(原始出版于 1994 年)
- Cut-the-knot 网站上的 Cantor Sets 和 Cantor Set and Function*
- Platonic Realms 网站上的 Cantor Set
友情链接: 超理论坛 | ©小时科技 保留一切权利