笛卡儿积（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

图
图 1：集合 \( \{x, y, z\} \) 和 \( \{1, 2, 3\} \) 的笛卡尔积

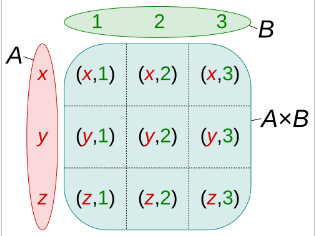
　　 在数学中，特别是集合论中，两个集合 \(A\) 和 \(B\) 的笛卡尔积，记作 \( A \times B \)，是所有有序对 \( (a, b) \) 的集合，其中 \( a \in A \)，且 \( b \in B \)\(^\text{[1]}\)。用集合构造符号表示为： \[ A \times B = \{ (a, b) \mid a \in A \text{ 且 } b \in B \}.^\text{[2][3]}~ \] 可以通过对 “行的集合” 与 “列的集合” 取笛卡尔积来创建一个表格。若取笛卡尔积 rows × columns，那么表格的每个单元格就包含一个形如（行值，列值）的有序对。\(^\text{[4]}\)

　　 同样地，也可以定义 \(n\) 个集合的笛卡尔积，称为 n 重笛卡尔积，它可以表示为一个 \(n\)-维数组，其中每个元素是一个 \(n\) 元组（n-tuple）。有序对是 2 元组（2-tuple）或称为 “偶对”。更一般地，还可以定义一个按索引排列的集合族的笛卡尔积。

　　 笛卡尔积的名称来自于勒内·笛卡尔，\(^\text{[5]}\) 他对解析几何的建立促成了这一概念的产生，该概念进一步推广后形成了 “直积” 的形式。

1. 集合论中的定义

　　 要对笛卡尔积进行严格的定义，必须在集合构造符号中指定一个定义域。在这种情况下，定义域必须包含笛卡尔积本身。

　　 对于集合 \( A \) 和 \( B \) 的笛卡尔积，若使用典型的 Kuratowski 对的定义，即将有序对 \( (a, b) \) 定义为 \((a, b) = \{\{a\}, \{a, b\}\}\) 那么一个合适的定义域是幂集的幂集 \(\mathcal{P}(\mathcal{P}(A \cup B))\) 其中 \( \mathcal{P} \) 表示幂集运算符（即某集合所有子集的集合）。

　　 于是，集合 \( A \) 和 \( B \) 的笛卡尔积可以定义为： \[ A \times B = \{ x \in \mathcal{P}(\mathcal{P}(A \cup B)) \mid \exists a \in A,\ \exists b \in B,\ x = (a, b) \}~ \] 也就是说，笛卡尔积是所有属于该幂集的集合 \( x \)，其中 \( x \) 是某个 \( a \in A \)、\( b \in B \) 所构成的 Kuratowski 有序对。

2. 示例

一副扑克牌

图
图 2：标准的 52 张扑克牌

　　 一个直观的例子是一副标准的 52 张扑克牌。标准扑克牌的点数集合为{A, K, Q, J, 10, 9, 8, 7, 6, 5, 4, 3, 2}，共有 13 个元素；花色集合为 {♠, ♥, ♦, ♣}，共有 4 个元素。这两个集合的笛卡尔积将产生一个包含 52 个有序对的集合，对应于全部 52 张可能的扑克牌。

　　 点数 × 花色的笛卡尔积得到的集合如下形式： {(A, ♠), (A, ♥), (A, ♦), (A, ♣), (K, ♠), \(\ldots\), (3, ♣), (2, ♠), (2, ♥), (2, ♦), (2, ♣)}

　　 花色 × 点数的笛卡尔积则得到如下形式的集合：{(♠, A), (♠, K), (♠, Q), (♠, J), (♠, 10), \(\ldots\), (♣, 6), (♣, 5), (♣, 4), (♣, 3), (♣, 2)}

　　 这两个集合是不同的，甚至是不相交的，因为它们的有序对元素次序不同。但它们之间存在一个自然的双射（一一对应关系），例如(3, ♣)对应于(♣, 3)，以此类推。

二维坐标系

图
图 3：示例点的笛卡尔坐标

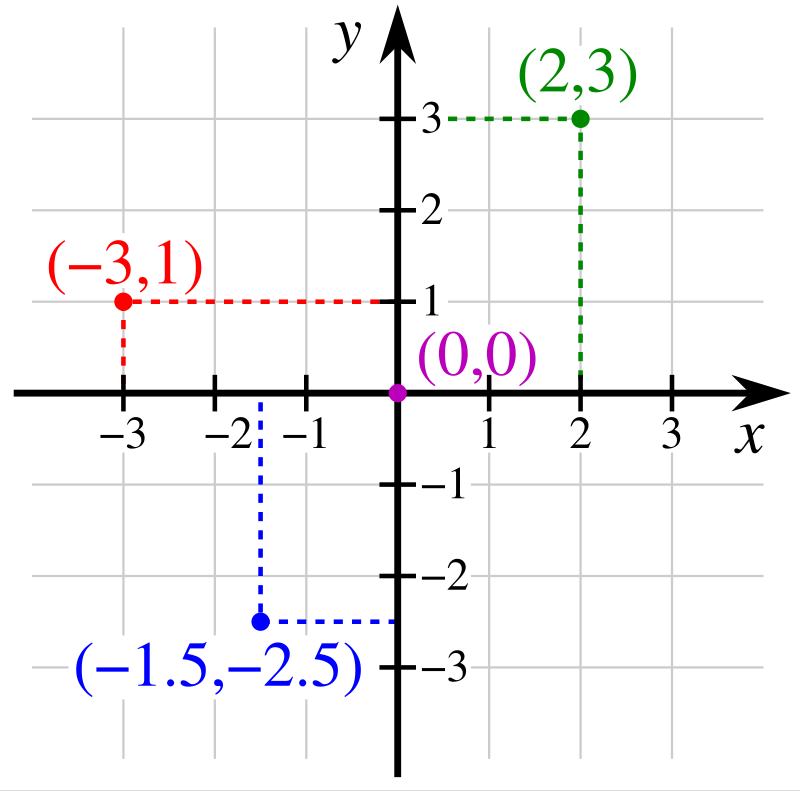
　　 历史上最著名的例子是解析几何中的笛卡尔平面。为了以数值方式表示几何图形，并从图形的数值表示中提取数据信息，勒内·笛卡尔将平面上的每个点对应一个实数对，称为该点的坐标。通常，这对数中的第一个分量和第二个分量分别称为该点的 \(x\) 坐标和 \(y\) 坐标（见图示）。

　　 所有这类数对的集合（即笛卡尔积 \( \mathbb{R} \times \mathbb{R} \)，其中 \( \mathbb{R} \) 表示实数集）就对应于整个平面上的点集。\(^\text{[7]}\)

3. 最常见的实现方式（集合论）

　　 从集合论的基本原理出发，可以对笛卡尔积进行形式化定义，这依赖于对有序对的定义。最常见的有序对定义是 Kuratowski 的定义，即：\((x, y) = \{\{x\}, \{x, y\}\}\) 根据这个定义，任意有序对 \( (x, y) \) 是集合 \(\mathcal{P}(\mathcal{P}(X \cup Y))\) 的元素，其中 \( \mathcal{P} \) 表示幂集运算符。因此，集合 \( X \times Y \) 是这个集合的子集。 在 ZFC（Zermelo–Fraenkel 集合论带选择公理）体系中，两个集合的笛卡尔积的存在性可以从配对公理、并集公理、幂集公理和分离公理推出。由于函数通常被定义为一种特殊的关系，而关系又通常被定义为笛卡尔积的子集，因此两个集合笛卡尔积的定义在逻辑上优先于多数其他数学对象的定义。

非交换性与非结合性

　　 设 \( A \)、\( B \)、\( C \)、\( D \) 为集合。

　　 笛卡尔积 \( A \times B \) 不是交换的，即 \[ A \times B \ne B \times A,~ \] 因为有序对中的元素顺序被颠倒了，除非满足以下条件之一：\(^\text{[8]}\)

　　 例如：

　　 设 \( A = \{1, 2\} \)，\( B = \{3, 4\} \) \[ A \times B = \{1, 2\} \times \{3, 4\} = \{(1,3), (1,4), (2,3), (2,4)\}~ \] \[ B \times A = \{3, 4\} \times \{1, 2\} = \{(3,1), (3,2), (4,1), (4,2)\}~ \]

　　 若 \( A = B = \{1, 2\} \) \[ A \times B = B \times A = \{1, 2\} \times \{1, 2\} = \{(1,1), (1,2), (2,1), (2,2)\}~ \]

　　 若 \( A = \{1, 2\} \)，\( B = \varnothing \)（空集） \[ A \times B = \{1, 2\} \times \varnothing = \varnothing ~ \] \[ B \times A = \varnothing \times \{1, 2\} = \varnothing ~ \]

　　 严格来说，笛卡尔积也**不是结合的**（除非所涉及的某个集合是空集）： \[ (A \times B) \times C \ne A \times (B \times C)~ \] 例如，若 \( A = \{1\} \)，则：\((A \times A) \times A = \{((1,1),1)\} \ne \{(1,(1,1))\} = A \times (A \times A)\)

交集、并集与子集

图
图 4

　　 笛卡尔积在交集方面满足如下性质（见中间图）： \[ (A \cap B) \times (C \cap D) = (A \times C) \cap (B \times D)~ \] 但在大多数情况下，若将交集替换为并集，上述等式则**不成立**（见最右侧图）： \[ (A \cup B) \times (C \cup D) \ne (A \times C) \cup (B \times D)~ \] 实际上，有如下恒等式成立： \[ (A \times C) \cup (B \times D) = [(A \setminus B) \times C] \cup [(A \cap B) \times (C \cup D)] \cup [(B \setminus A) \times D]~ \] 对于差集，还有以下恒等式： \[ (A \times C) \setminus (B \times D) = [A \times (C \setminus D)] \cup [(A \setminus B) \times C]~ \] 以下是展示笛卡尔积与其他运算符分配律的一些规则（见最左侧图）\(^\text{[8]}\)： \[ \begin{aligned} A \times (B \cap C) &= (A \times B) \cap (A \times C), \\ A \times (B \cup C) &= (A \times B) \cup (A \times C), \\ A \times (B \setminus C) &= (A \times B) \setminus (A \times C), \end{aligned}~ \] 补集方面，有如下等式： \[ (A \times B)^{\complement} = (A^{\complement} \times B^{\complement}) \cup (A^{\complement} \times B) \cup (A \times B^{\complement}),~ \] 其中 \( A^{\complement} \) 表示集合 \( A \) 的绝对补集。

　　 关于子集关系，还满足以下性质：

　　 若 \( A \subseteq B \)，则 \[ A \times C \subseteq B \times C~ \] 若 \( A \ne \varnothing \)，\( B \ne \varnothing \)，则 \(A\times B \subseteq C \times D \iff A \subseteq C\) 且 \(B \subseteq D\).\(\text{[9]}\)

基数

　　 集合的基数指的是集合中元素的数量。例如，定义两个集合： \( A = \{a, b\} \)，\( B = \{5, 6\} \)， 集合 \( A \) 和 \( B \) 都各有两个元素。它们的笛卡尔积，记作 \( A \times B \)，会得到一个新集合，其元素如下：

　　 \[ A \times B = \{(a,5), (a,6), (b,5), (b,6)\}~ \]

　　 也就是说，集合 \( A \) 中的每个元素都与集合 \( B \) 中的每个元素配对，并且每一个配对形成输出集合中的一个元素。 生成的每个元素包含的值个数，等于参与笛卡尔积的集合数量——在本例中是 2。输出集合的基数等于所有输入集合基数的乘积，即： \[ |A \times B| = |A| \cdot |B|^\text{[4]}~ \] 在本例中：\(|A \times B| = 4\)

　　 类似地， \[ |A \times B \times C| = |A| \cdot |B| \cdot |C|~ \] 依此类推。

　　 如果 \( A \) 或 \( B \) 是无限集合，而另一个集合非空，那么它们的笛卡尔积 \( A \times B \) 也是无限集合。\(^\text{[10]}\)

4. 多个集合的笛卡尔积

n 元笛卡尔积

　　 笛卡尔积可以推广为 \( n \) 个集合 \( X_1, \dots, X_n \) 的 \(n\) 元笛卡尔积，定义为： \[ X_1 \times \cdots \times X_n = \{(x_1, \dots, x_n) \mid x_i \in X_i \text{ 对于每个 } i \in \{1, \dots, n\} \}~ \] 这个集合的元素是 \( n \)-元组（n-tuples）。如果元组被定义为嵌套的有序对，那么它可以写作 \((X_1 \times \cdots \times X_{n-1}) \times X_n\) 的形式。

　　 如果元组被定义为一个函数： \[ x: \{1, 2, \dots, n\} \to X_1 \cup \cdots \cup X_n~ \] 并且要求对于每个 \( i \in \{1, \dots, n\} \)，都有 \( x(i) \in X_i \)，那么 \(n\) 元笛卡尔积也可以定义为以下函数的集合： \[ \left\{ x: \{1, \dots, n\} \to X_1 \cup \cdots \cup X_n\ \middle|\ x(i) \in X_i \text{ 对于每个 } i \in \{1, \dots, n\} \right\}~ \]

n 元笛卡尔幂

　　 集合 \( X \) 的笛卡尔平方是它与自身的笛卡尔积，记作 \( X^2 = X \times X \)。一个例子是二维平面 \( \mathbf{R}^2 = \mathbf{R} \times \mathbf{R} \)，其中 \( \mathbf{R} \) 是实数集：\(^\text{[1]}\)\( \mathbf{R}^2 \) 是所有点 \( (x, y) \) 的集合，其中 \( x \) 和 \( y \) 是实数（见笛卡尔坐标系）。

　　 集合 \( X \) 的 \(n\) 元笛卡尔幂，记作 \( X^n \)，定义如下： \[ X^n = \underbrace{X \times X \times \cdots \times X}_{n} = \{(x_1, \dots, x_n) \mid x_i \in X\ \text{对于每个 } i \in \{1, \dots, n\} \}~ \] 一个例子是 \( \mathbf{R}^3 = \mathbf{R} \times \mathbf{R} \times \mathbf{R} \)，其中 \( \mathbf{R} \) 仍是实数集，\(^\text{[1]}\) 更一般地是 \( \mathbf{R}^n \)。

　　 集合 \( X \) 的 \(n\) 元笛卡尔幂与从一个 \(n\) 元集合到 \( X \) 的函数空间是同构的。作为特例，集合 \( X \) 的 0 元笛卡尔幂可以定义为一个单元素集合，对应于定义域为空、余域为 \( X \) 的空函数。

交集、并集、补集与子集

　　 设有笛卡尔积： \[ A = A_1 \times \cdots \times A_n,\quad B = B_1 \times \cdots \times B_n~ \] 则有以下性质：

  1. 子集关系 \( A \subseteq B \iff A_i \subseteq B_i \quad \text{对于所有 } i = 1, 2, \ldots, n\)\(^\text{[11]}\)
  2. 交集：\(A \cap B = (A_1 \cap B_1) \times \cdots \times (A_n \cap B_n)\) 并且若存在某个 \( i \) 使得 \(A_i \cap B_i = \varnothing\) 则有 \(A \cap B = \varnothing\)\(^\text{[11]}\)
  3. 并集 \(A \cup B \subseteq (A_1 \cup B_1) \times \cdots \times (A_n \cup B_n)\) 且只有在以下情况下可能成立等号：\(^\text{[12]}\)
    • \( A \subseteq B \) 或 \( B \subseteq A \)；
    • 对于所有 \( i = 1, 2, \ldots, n \)，除一个以外都有 \( A_i = B_i \)。
  4. 补集：若定义全集为 \(U = X_1 \times \cdots \times X_n\), 则可以计算笛卡尔积 \(A = A_1 \times \cdots \times A_n\) 的补集 \(A^\complement \)。为简化表达，引入如下记号：用中括号表示笛卡尔积形成的元组，例如： \[ A = A_1 \times A_2 \times \cdots \times A_n = [A_1\quad A_2\quad \cdots\quad A_n]~ \]

　　 在 \(n\) 元组代数（n-tuple algebra, NTA）中，\(^\text{[12]}\) 这种类似矩阵的笛卡尔积表示方式称为 C-n 元组（C-n-tuple）。

　　 考虑到上述内容，在同一全集下，多个笛卡尔积的并集可以表示为一个用中括号括起来的 “矩阵”，其中每一行代表并集中参与的一个笛卡尔积： \[ A \cup B = (A_1 \times A_2 \times \cdots \times A_n) \cup (B_1 \times B_2 \times \cdots \times B_n) = \left[ \begin{array}{cccc} A_1 & A_2 & \cdots & A_n \\ B_1 & B_2 & \cdots & B_n \end{array} \right]~ \] 在 \(n\) 元组代数（NTA）中，这种结构称为一个 C-系统（C-system）。

　　 那么，笛卡尔积 \( A \) 的补集在全集 \[ U = X_1 \times X_2 \times \cdots \times X_n~ \] 中将表示为一个 \( n \times n \) 的矩阵型 C-系统如下： \[ A^\complement = \left[ \begin{array}{ccccc} A_1^\complement & X_2 & \cdots & X_{n-1} & X_n \\ X_1 & A_2^\complement & \cdots & X_{n-1} & X_n \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ X_1 & X_2 & \cdots & A_{n-1}^\complement & X_n \\ X_1 & X_2 & \cdots & X_{n-1} & A_n^\complement \end{array} \right]~ \] 其中，对角线上的分量 \( A_i^\complement \) 表示 \(X_i \setminus A_i\)

　　 在 \(n\) 元组代数（NTA）中，表示 C-n 元组 \( A \) 的补集的对角 C-系统 \( A^\complement \) 可以用一个反向中括号括起来的对角分量元组进行简洁表示：

　　 \[ A^\complement = ]A_1^\complement\quad A_2^\complement\quad \dots\quad A_n^\complement[~ \]

　　 这种结构被称为一个 D-n 元组（D-n-tuple）。

　　 如果一个 C-系统 \( R \) 给定，那么它的补集 \( R^\complement \) 是一个与 \( R \) 同维度的矩阵结构，用反向中括号括起，并且其中所有元素都等于原始矩阵中各分量的补集。这样的结构称为一个 D-系统（D-system），必要时可通过其中包含的 D-n 元组的交集来计算。

　　 例如，若给定如下的 C-系统： \[ R_1 = \left[ \begin{array}{cccc} A_1 & A_2 & \dots & A_n \\ B_1 & B_2 & \dots & B_n \end{array} \right]~ \] 那么它的补集是： \[ R_1^\complement = \left] \begin{array}{cccc} A_1^\complement & A_2^\complement & \dots & A_n^\complement \\ B_1^\complement & B_2^\complement & \dots & B_n^\complement \end{array} \right[~ \] 接下来我们将讨论一些在研究 NTA 性质过程中得到的、与笛卡尔积结构有关的新关系式。\(^\text{[12]}\) 在同一全集中定义的这些结构被称为 同类型结构。

  1. C-系统的交集设有两个同类型的 C-系统 \( P \) 和 \( Q \)。 它们的交集是一个新的 C-系统，包含了 \( P \) 中每一个 C-n 元组与 \( Q \) 中每一个 C-n 元组之间所有非空交集所构成的 C-n 元组。
  2. 检查 C-n 元组是否包含于 D-n 元组,设有 C-n 元组 \(P = [P_1\quad P_2\quad \cdots \quad P_N]\) 和 D-n 元组 \[ Q = ]Q_1\quad Q_2\quad \cdots \quad Q_N[~ \] 则有：\(P \subseteq Q \iff \text{至少存在一个 } i \text{ 使得 } P_i \subseteq Q_i\) 换句话说，当且仅当在某一维上 \( P_i \subseteq Q_i \)，就可以认为整个 C-n 元组 \( P \) 包含于 D-n 元组 \( Q \)。
  3. 检查 C-n 元组是否包含于 D-系统,设有 C-n 元组 \( P \) 和 D-系统 \( Q \)，则有：\(P \subseteq Q \iff \) 对于 \(Q\) 中的每一个 D-n 元组 \(Q_i\)，均有 \(P \subseteq Q_i\) 换句话说，当且仅当 \( P \) 被包含于 D-系统中所有的 D-n 元组中，才有 \( P \subseteq Q \) 成立。

无限笛卡尔积

　　 可以定义一个任意（可能是无限）索引的集合族的笛卡尔积。设 \( I \) 是任意的索引集合，且 \( \{X_i\}_{i \in I} \) 是由 \( I \) 索引的集合族，那么这些集合的笛卡尔积定义为： \[ \prod_{i \in I} X_i = \left\{ f : I \to \bigcup_{i \in I} X_i \mid \forall i \in I, \, f(i) \in X_i \right\}~ \] 也就是说，这是定义在索引集 \( I \) 上的所有函数的集合，其中该函数在每个特定的索引 \( i \) 处的值是集合 \( X_i \) 的一个元素。即使每个 \( X_i \) 都是非空的，笛卡尔积也可能是空的，如果不假设选择公理（该公理等价于每个此类积都是非空的）。\(\prod_{i \in I} X_i\) 也可以表示为：\(X_{i \in I} X_i\)\(^\text{[13]}\)

　　 对于每个 \( j \in I \)，定义函数 \[ \pi_j: \prod_{i \in I} X_i \to X_j,~ \] 由 \(\pi_j(f) = f(j)\) 给出，称为第 \( j \) 个投影映射。

　　 笛卡尔幂是所有因子 \( X_i \) 都是相同集合 \( X \) 的笛卡尔积。在这种情况下， \[ \prod_{i \in I} X_i = \prod_{i \in I} X~ \] 是从 \( I \) 到 \( X \) 的所有函数的集合，通常表示为 \( X^I \)。这种情况在基数指数运算的研究中很重要。一个重要的特例是当索引集是自然数集 \( \mathbb{N} \) 时：这个笛卡尔积就是所有无限序列的集合，其中第 \( i \) 项位于相应的集合 \( X_i \) 中。例如， \[ \prod_{n=1}^{\infty} \mathbb{R} = \mathbb{R} \times \mathbb{R} \times \cdots~ \] 可以被看作是一个具有可数无限个实数分量的向量。这个集合通常表示为 \( \mathbb{R}^\omega \) 或 \( \mathbb{R}^{\mathbb{N}} \)。

5. 其他形式

简化形式

　　 如果多个集合被一起相乘（例如 \( X_1, X_2, X_3, \dots \)），一些作者 \(^\text{[14]}\) 选择将笛卡尔积简写为 \( \times X_i \)。

函数的笛卡尔积

　　 如果 \( f \) 是从 \( X \) 到 \( A \) 的函数，\( g \) 是从 \( Y \) 到 \( B \) 的函数，则它们的笛卡尔积 \( f \times g \) 是从 \( X \times Y \) 到 \( A \times B \) 的一个函数，满足： \[ (f \times g)(x, y) = (f(x), g(y))~ \] 这可以扩展到元组和无限集合的函数。它与将函数视为集合的标准笛卡尔积不同。

柱体

　　 设 \( A \) 是一个集合，且 \( B \subseteq A \)。则关于 \( A \) 的 \( B \) 的柱体是 \( B \times A \) 的笛卡尔积。

　　 通常情况下，\( A \) 被认为是上下文中的全集，因此省略不写。例如，如果 \( B \) 是自然数集 \( \mathbb{N} \) 的子集，则 \( B \) 的柱体是 \( B \times \mathbb{N} \)。

6. 集合论之外的定义

范畴理论

　　 尽管笛卡尔积传统上应用于集合，范畴理论为数学结构的积提供了更为一般的解释。这与范畴理论中的**笛卡尔平方**概念不同，但相关联，笛卡尔平方是纤维积的推广。

　　 指数运算是笛卡尔积的右伴随；因此，任何具有笛卡尔积（和最终对象）的范畴都是笛卡尔闭范畴。

图论

　　 在图论中，两个图 \( G \) 和 \( H \) 的笛卡尔积是一个图，记作 \( G \times H \)，其顶点集是 \( V(G) \times V(H) \)，并且两个顶点 \( (u, v) \) 和 \( (u', v') \) 在 \( G \times H \) 中相邻，当且仅当 \( u = u' \) 且 \( v \) 在 \( H \) 中与 \( v' \) 相邻，或 \( v = v' \) 且 \( u \) 在 \( G \) 中与 \( u' \) 相邻。图的笛卡尔积不是范畴理论意义上的积。相反，范畴积称为图的张量积。

7. 另见

8. 参考文献

  1. Weisstein, Eric W. "笛卡尔积"。MathWorld。2020 年 9 月 5 日检索。
  2. Warner, S. (1990). 《现代代数》。Dover Publications，第 6 页。
  3. Nykamp, Duane. "笛卡尔积定义"。Math Insight。2020 年 9 月 5 日检索。
  4. "笛卡尔积"。web.mnstate.edu。2020 年 7 月 18 日存档。2020 年 9 月 5 日检索。
  5. "Cartesian"。Merriam-Webster.com。2009 年。2009 年 12 月 1 日检索。
  6. Corry, S. "集合论的基本概述"（PDF）。2023 年 5 月 5 日检索。
  7. Goldberg, Samuel (1986). 《概率论：简介》。Dover 数学丛书。Courier Corporation，第 41 页。ISBN 9780486652528。
  8. Singh, S. (2009 年 8 月 27 日). "笛卡尔积"。来自 Connexions 网站: http://cnx.org/content/m15207/1.5/
  9. "笛卡尔积的子集"（2011 年 2 月 15 日）。ProofWiki。2011 年 8 月 1 日 05:06 检索自 https://proofwiki.org/w/index.php?title=Cartesian_Product_of_Subsets&oldid=45868
  10. Peter S. (1998). 《无限集合数学速成课程》。St. John's Review, 44(2), 35–59。2011 年 8 月 1 日检索自 http://www.mathpath.org/concepts/infinity.htm
  11. Bourbaki, N. (2006). 《集合论》。Springer，第 E II.34–E II.38。
  12. Kulik, B.; Fridman, A. (2022). 《基于简单数学的复杂逻辑分析方法》。剑桥学者出版。ISBN 978-1-5275-8014-5。
  13. F. R. Drake, 《集合论：大基数导论》，第 24 页。逻辑与数学基础研究丛书，第 76 卷（1978 年）。ISBN 0-7204-2200-0。
  14. Osborne, M. 和 Rubinstein, A.，1994 年。《博弈论教程》。MIT 出版社。

9. 外部链接


致读者： 小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此，我们请求广大读者热心打赏 ，使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损， 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款， 他们的付出帮助了 99% 的读者免费获取知识， 我们在此表示感谢。

                     

友情链接： 超理论坛　|　©小时科技 保留一切权利