中国科学院 2018 年考研普通物理

贡献者： Entanglement

　　 声明：“该内容来源于网络公开资料，不保证真实性，如有侵权请联系管理员”

1. 选择题

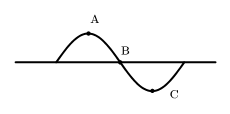
1. 某时刻的弦波如图所示，在此弦段中，振动动能最大的部位为
   A. A 处 $\quad$ B. B 处 $\quad$ C. C 处 $\quad$ C. A 和 C 处 $\quad$
   
   图 1：选择题 1 图示
2. 以下关于质点系描述正确的是
   A. 质点系质心运动只与只与质点系所受合内力有关，质点系的内力不可能改变质点系的总动能。
   B. 质点系质点运动只与质点系所受合外力有关，质点系的内力可以改变质点系的总动能。
   C. 质点系质点运动只与质点所受合内力有关，质点系的内力可以改变质点系的总动能。
   D. 质点系质点运动只与质点系所受合外力有关，质点系的内力不可以改变质点系的总动能。
   
6. 关于磁化电流与传导电流，下面说法不正确的是
   A。磁化电流是大量分子电流统计平均的宏观效果，传导电流是电荷迁移的结果
   B. 磁化电流和传导电流都能产生磁场
   C. 磁化电流和传导电流都能产生焦耳热
   C. 磁化电流产生的磁场服从安培环路定律
   
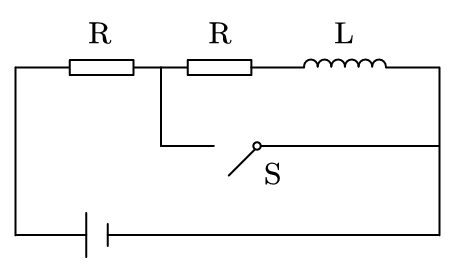
7. 一电路如下图所示，两电阻大小均为 $R$，电感 $L$，电源电动势 $\epsilon$ 开关 $S$ 闭合后电感 $L$ 上的电流 $i$ 随时间的变化关系为
   A. $i = \frac{\epsilon}{2R}$
   B. $i = \frac{\epsilon}{R}e^{-\frac{2R}{L}t}$
   C. $i = \frac{\epsilon}{2R}e^{-\frac{R}{L}t}$
   C. $i = \frac{\epsilon}{2R}(1-e^{-\frac{R}{L}t})$
   
   
   图 2：选择题 7 图示
8. 原子态 $^{1}D_{1}$ 的能级在磁感应强度 $ \boldsymbol{\mathbf{B}} $ 的弱磁场中分裂成多少子能级？
   A. 3 个 $\quad$ B. 2 个 $\quad$ C. 5 个 $\quad$ C. 4 个 $\quad$

2. 简答题

1. 所谓的二体问题，是指两个指点只有相互作用力，不受外力，对于二体问题，试推导一个质点相对于另一个质点的运动学方程。
   对比 $ \boldsymbol{\mathbf{F}} = \mu \boldsymbol{\mathbf{a}} $ 形式，请写出 $\mu$ 的表达式（$\mu$ 代表二体约化质量）
2. 圆盘上有一圈带正电的带点球，问中间的螺线管断电时，圆盘是否会转动，如何转，为什么。
3. 牛顿环，凸透镜和平面介质的折射率分别为 $n_{1}$ $n_{3}$，中间为空气，此时牛顿环中心为暗纹。若在中间注入一种液体，折射率在凸透镜和平面介质中间。$n_{1}>n_{2}>n_{3}$，此时中心为什么纹，说明原因。

3.

　　 太阳系某一小行星的抛物线轨道方程可表述为 $y^{2} = 4Cx$ ,太阳位于焦点 $x = C$，$y = 0$ 处，将太阳质量记为 $M$，求：
(1) 小行星在抛物线顶点处的速率；
(2) 小行星在抛物线顶点处的曲率半径；
(3) 小行星在抛物线顶点处的角动量与其质量的比值。

4.

　　 狐狸沿半径为 $R$ 的圆轨道以速率 $v$ 奔跑，在狐狸出发的同时，猎犬从圆心出发，以相同的速率追击狐狸。在追击过程中，圆心、狐狸和猎犬始终连成一条直线，以圆心 $O$ 为原点，从 $O$ 点到狐狸初始位置连线为极轴，建立极坐标系。
(1) 导出猎犬速度矢量与径向位置 $r$ 的关系；
(2) 导出猎犬加速度矢量与径向位置 $r$ 的关系；
(3) 确定猎犬的轨道方程。

5.

　　 如图所示，电子感应加速器是利用变化的磁场 $ \boldsymbol{\mathbf{B}} $ 所产生的感应电场（漩涡电场）$ \boldsymbol{\mathbf{E}} $ 来加速电子，同时磁场本身又维持电子在固定的圆轨道上运动，设开始时，磁感应强度 $B$ 为 0，电子的初速度为 0；变化的磁场 $ \boldsymbol{\mathbf{B}} $ 经过一段时间加速电子后，电子轨道处的的磁感应强度大小为 $B_{0}$，电子轨道内的平均磁感应强度大小为 $ \boldsymbol{\mathbf{B}} = $