中国科学院 2020 年考研普通物理

贡献者： Entanglement

　　 声明：“该内容来源于网络公开资料，不保证真实性，如有侵权请联系管理员”

1. 单项选择题（共 32 分，每小题 4 分）

1. 简谐振动微分方程 $\ddot{x}+{\omega}^2{x}=0$ 满足的变换不变性不包括
   A. 时间反演
   B. 时间平移
   C. 空间反射
   D. 空间加速平移
   
2. 在高空走钢丝者手持长杆作为辅助，所应用的物理原理是
   A. 长杆很重，走钢丝者手持长杆有一种踏实的感觉；
   B. 长杆的转动惯量对运动的平衡作用；
   C. 长杆对分的平衡能力；
   D. 走钢丝者的体重加上长杆的重量，增加了运动的惯性。
   
3. 对于惯性系 $S$，一飞船以船头向前且速度为 0.8$c$($c$ 为光速)匀速运动。飞船的静长为 $l$，飞船的船头朝船尾发出一束光，并被位于船尾的接收器接收到，$S$ 系中的观察者认为从船头发出光到船尾接收到光的时间间隔为
   A. $\frac{l}{c}$
   B. $\frac{l}{3c}$
   C. $\frac{0.6l}{c}$
   D. $\frac{l}{1.8c}$
   
4. 三个点电荷分别位于边长为 $a$ 的正三角形的三个顶点，它们的电荷量分别为 $q$，$q$ 和 $-4q$。真空介电常数为 $\epsilon_{0}$，则这个系统的总静电能为（设相距无穷远时相互作用能为零）
   A. $-5q^{2}/2\pi \epsilon_{0} a$
   B. $-5q^{2}/4\pi \epsilon_{0} a$
   C. $-7q^{2}/4\pi \epsilon_{0} a$
   D. $-7q^{2}/2\pi \epsilon_{0} a$
   
5. 将一点电荷从无穷远处沿径向逐渐靠近到一带电的均匀材质导体球表面，下列论述正确的时
   A. 如果点电荷与导体球所带总电荷同号，移动过程中两者之间总是相互排斥；如果点电荷与导体球所带总电荷异号，移动过程中两者之间总是相互吸引
   B. 如果点电荷与导体球所带总电荷同号，移动过程中两者之间从相互排斥变成相互吸引；如果点电荷与导体球所带总电荷异号，移动过程中两者之间总是相互吸引
   C. 如果点电荷与导体球所带总电荷同号，移动过程中两者之间总是相互排斥；如果点电荷与导体球所带总电荷异号，移动过程中两者之间从相互吸引变成相互排斥
   D. 根据电量大小的不同，（A）、（B）或（C）三种情况都可能出现
   
6. 有一半径为 $R$ 的单匝圆线圈，通以顺时针电流 $I$。若将该导线弯成匝数 $N=2$ 的平面线圈，导线总长度保持不变，通以同样大小的电流 $I$，并且在两匝线圈中电流方向仍同为顺时针，则线圈中心的磁感应强度和线圈的磁矩分别是原来的
   A. 4 倍和 1/8
   B. 4 倍和 1/2
   C. 2 倍和 1/4
   D. 2 倍和 1/2
   
7. 以下选项中，最接近理想气体的是
   A. 低温高压气体
   B. 低温低压气体
   C. 高温低压气体
   D. 气液共存时的气体
   
8. 假设一个原子的某一多重态的五个能级遵循 $LS$ 耦合，且按照能量递增的顺序，相邻两个能级的间隔比为 $1:2:3:4$。那么这些能级的量子数 $S'$，$L'$ 分别为
   A. 2,2;
   B. 2,3;
   C. 1,0;
   D. 3,2;
   

2. 简答题（共 30 分）

1. （12 分）伽利略变换是在非相对论极限下惯性系之间的变换，因而伽利略变换在经典力学中有着十分基础的地位。坐标系 $x'y'z'$ 沿 $x$ 轴方向以匀速 $v$ 相对于已知惯性系 $xyz$ 运动，请：
   (1)给出伽利略变换的公式，忽略坐标系基底转动的变换；
   (2)简要证明在伽利略变换后，牛顿第二定律在两个坐标系中的形式相同，也即牛顿第二定律对伽利略变换是不变的。
   
2. (10 分)请说明处在变化磁场中的导体上不同位置间的电势差来源。
3. (8 分)一束光线从折射率为 $n_{1}$ 的介质入射到折射率为 $n_{2}$ 的介质（设 $n_{1}< n_{2}$）,在两种介质的界面有反射和折射现象。在处理光的反射问题时，简述费马原理和菲涅耳公式各得到哪些主要结论。

3.

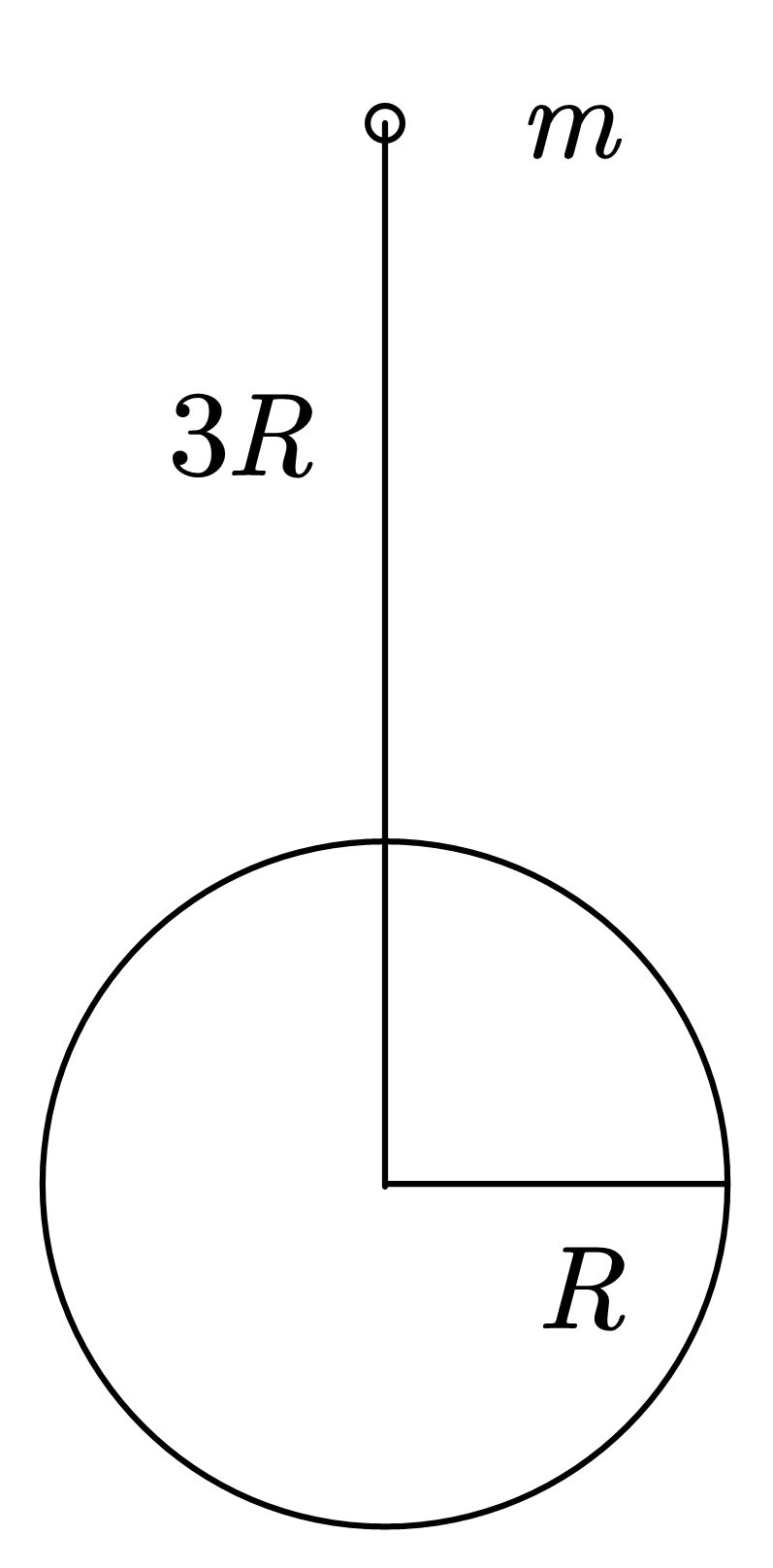
　　 （共 20 分）如图所示，离地心 $3R$($R$ 为地球半径)处有一质量为 $m$ 的飞船，绕地球作匀速圆周运动，问：
(1) 它的运行速度大小 $v_{0}$ 为多少？
(2) 飞船在此处要将它的运动速度大小至少增加到 $v_{1}$ 为多少时，它才能飞离地球？
(3) 飞船在 $3R$ 处，速度大小瞬间增加到 $v_{1}$ 后（方向不变）关闭发动机，则在飞离地球的过程中，离地心为 $12R$ 处，它的切向加速度大小 $a_{t}$ 为多少？该处轨道的曲率半径 $\rho$ 为多少？
注：以上各答案都用地球半径 $R$ 以及地球表面附近的重力加速度 $g$ 来表示。

4.

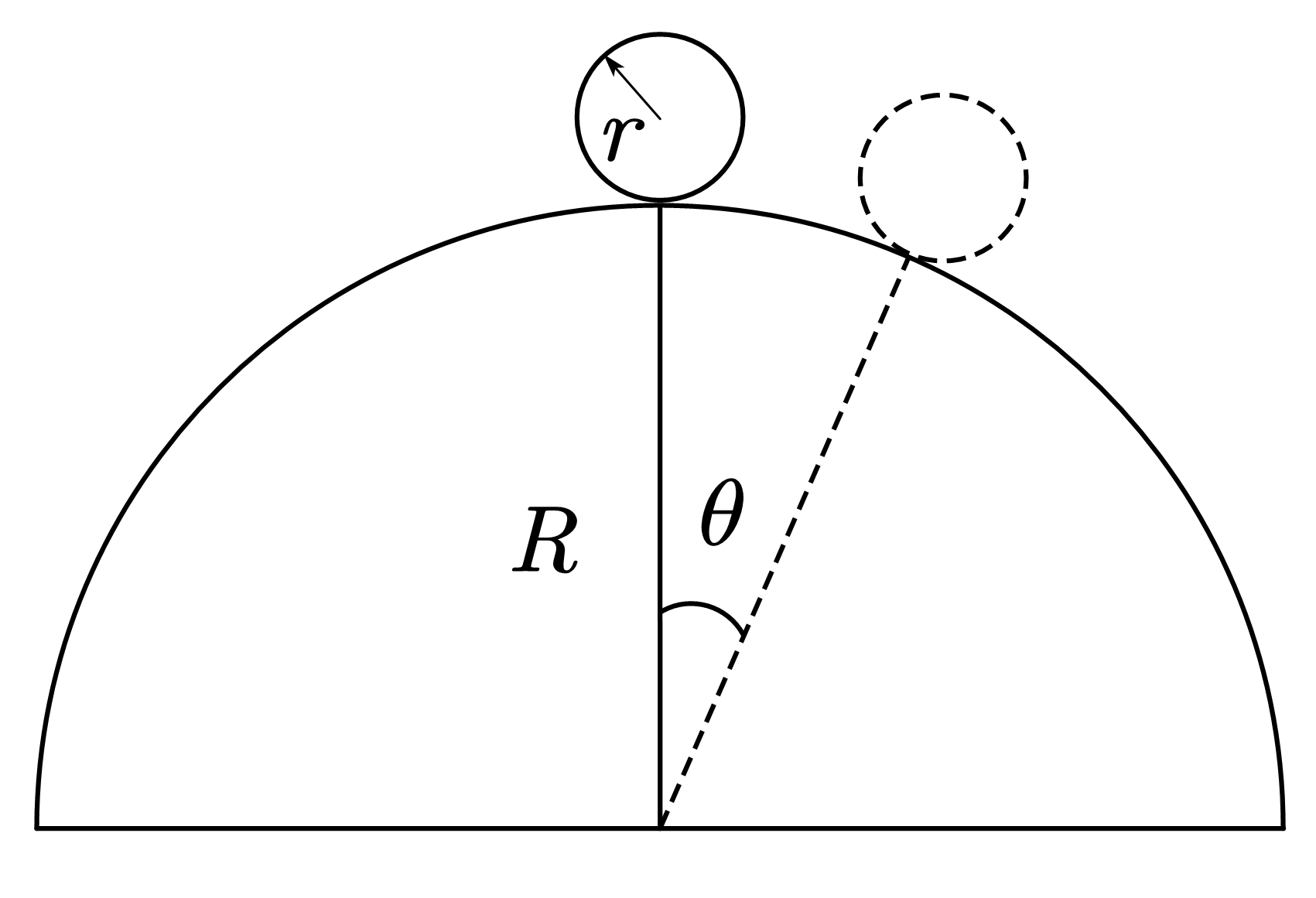
　　 （共 20 分）如图所示，质量为 $m$、半径为 $r$ 的匀质小球从截面半径为 $R$ 的固定圆柱面顶端自静止开始滚动，为保证小球在 $\theta \le 45^{\circ}$ 的范围内作无滑动的纯滚动，试求小球与柱面的摩擦因数 $\mu$ 的取值范围。(提示：匀质小球过球心的转动惯量为 $\frac{2}{5} mr^{2}$)

5.

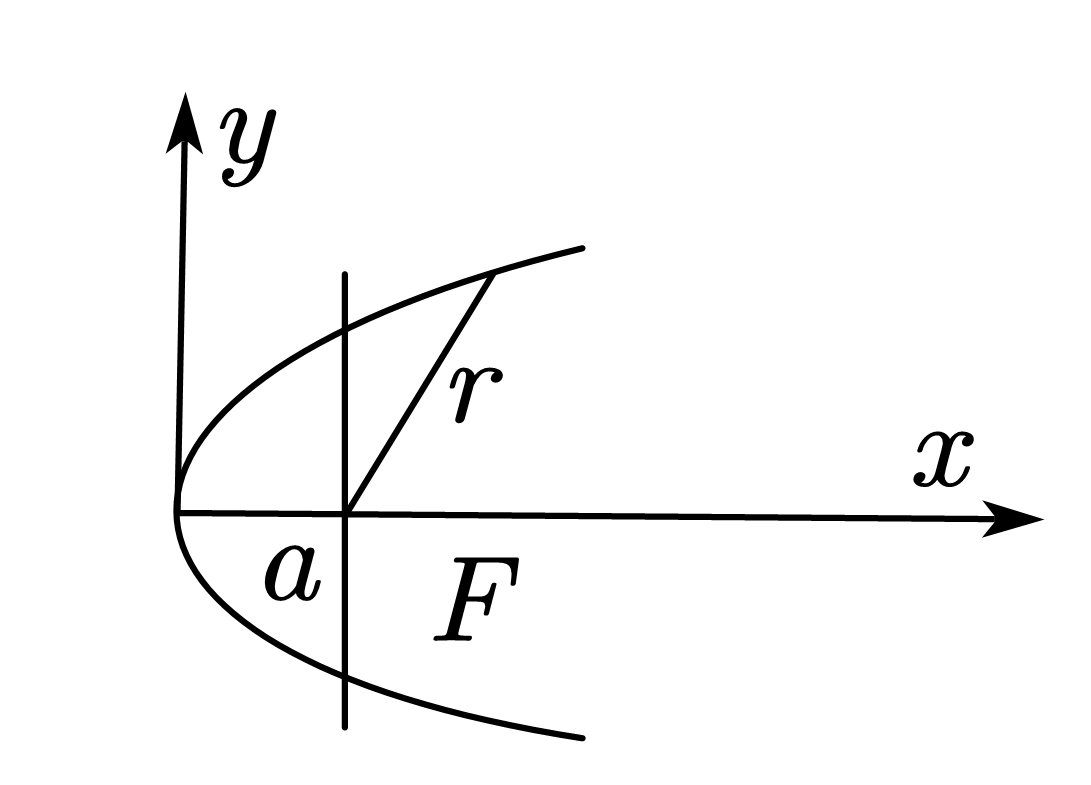
　　 （共 20 分）如图所条无穷长的导线载有电流 $I$，该导线弯成一抛物线形状，焦点到顶点的距离为 $a$，在图示 $xy$ 坐标系中，该抛物线的曲线方程为 $y^{2}=4ax$ 焦点 $F$ 在此坐标系中坐标为 $(x,y)=(a,0)$，真空中的磁导率为 $\mu_{0}$，求焦点 $F$ 处的磁感应强度 $B$。

6.

　　 （共 20 分）球形电容器由半径为 $R_1$ 的导体球和与它同心半径为 $R_2$ 的导体球壳构成，$R_1< R_2$。其间充满电介质，介质的介电常数是变化的，在 $R_1$ 处相对介电常数为 $\epsilon_1$，在 $R_2$ 处相对介电常数为 $\epsilon_2$，半径 $R_1$ 到 $R_2$ 之间电介质的相对介电常数随半径的变化而连续线性从 $\epsilon_1$ 变化到 $\epsilon_2$。内球带自由电荷 $Q$。
(1)求介质中的电场分布。
(2)作半径为 $R_{3}=12$ 的球面（球心与导体球相同）,求此球面内的电荷总量。

7.

　　 （共 8 分）在如图所示杨氏干涉装置中，双缝间距为 $a$，屏幕至双缝的距离为 $d$，有两个亮度相同、彼此不相干、波长都为 $l$ 的点光源 $S_1$ 与 $S_2$，其中 $S_1$ 在对称轴上固定不动，$S_2$ 在 $S_1$ 之上距离为 $x$ 处，两点光源至双缝的距离为 $R$。根据几何推导可以得知，单独由点光源 $S_2$ 产生的干涉条纹相对于单独由点光源 $S_1$ 产生的干涉条纹会往方移动，移动距离为 $\Delta x'=D_{x}1R$ 已知 $d=0.2mm$、$D=100cm$、$R=20cm$、$\lambda =500nm$，试求当两点光源之间的距离 $x$ 至少为多少时，屏幕上的干涉条纹最不明显（即其中个光源的干涉明纹与另一个光源的干涉暗纹重合）。