费米-狄拉克统计（综述）

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 费米–狄拉克统计是一种适用于由许多不相互作用的相同粒子组成的系统的量子统计，这些粒子遵循泡利不相容原理。其结果是费米–狄拉克分布，描述了粒子在不同能量态上的分布。该统计方式以恩里科·费米和保罗·狄拉克命名，他们分别在 1926 年独立推导出了这一分布。\(^\text{[1][2]}\) 费米–狄拉克统计属于统计力学的范畴，并且基于量子力学的基本原理。

　　 费米–狄拉克统计适用于具有半整数自旋（\(1/2\)、\(3/2\) 等）的相同且不可区分的粒子，这些粒子被称为费米子，并处于热力学平衡状态。当粒子之间的相互作用可以忽略时，该系统可以用单粒子能级来描述。其结果是粒子在这些能级上的费米–狄拉克分布，其中任何两个粒子都不能占据相同的状态，这对系统的性质产生了重要影响。费米–狄拉克统计最常应用于电子，电子是一种自旋为 \(1/2\) 的费米子。

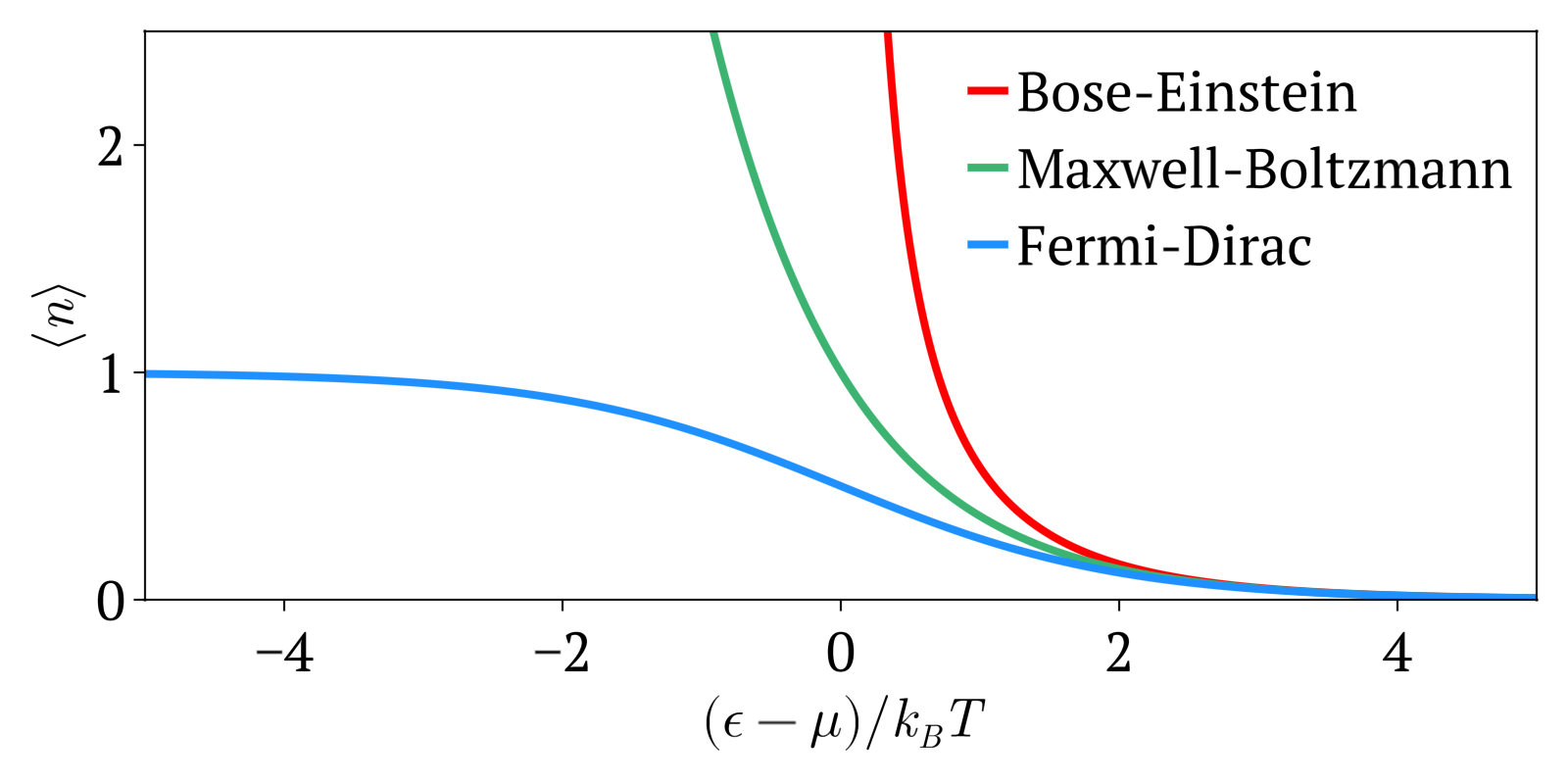
　　 费米–狄拉克统计的对应理论是玻色–爱因斯坦统计，它适用于具有整数自旋（0、1、2 等）的相同且不可区分的粒子，这些粒子被称为玻色子。在经典物理中，麦克斯韦–玻尔兹曼统计用于描述相同但可区分的粒子。与费米–狄拉克统计不同，在玻色–爱因斯坦统计和麦克斯韦–玻尔兹曼统计中，多个粒子可以占据相同的量子态。

1. 历史

　　 在 1926 年费米–狄拉克统计被引入之前，理解电子行为的一些方面十分困难，因为存在看似矛盾的现象。例如，在室温下，金属的电子比热容似乎仅由比导电电子数目少 100 倍的电子贡献。\(^\text{[3]}\) 此外，也难以解释为何在室温下对金属施加高电场所产生的发射电流几乎不依赖于温度。

　　 当时的德鲁德模型，即金属的电子理论，之所以遇到困难，是因为它假设**所有电子在经典统计理论下是等效的。换句话说，认为每个电子对比热的贡献约为**玻尔兹曼常数 \(k_B\) 的量级。然而，这一问题直到费米–狄拉克统计**的发展才得以解决。

　　 费米–狄拉克统计首次由恩里科·费米 \(^\text{[1]}\) 和保罗·狄拉克 \(^\text{[2]}\) 于 1926 年发表。据马克斯·玻恩所述，帕斯库尔·约当在 1925 年也提出了相同的统计方法，并将其称为 “泡利统计”，但未能及时发表。\(^\text{[4][5][6]}\) 据狄拉克所说，该统计方法最早是由费米研究的，因此他称其为 “费米统计”，并将遵循该统计的粒子称为 “费米子”\(^\text{[7]}\)

　　 1926 年，拉尔夫·福勒率先将费米–狄拉克统计应用于描述恒星塌缩成白矮星的过程。\(^\text{[8]}\)1927 年，阿诺德·索末菲将其应用于金属中的电子，并发展了自由电子模型。\(^\text{[9]}\)1928 年，福勒和洛塔·诺德海姆又将其应用于金属的场电子发射。\(^\text{[10]}\) 费米–狄拉克统计仍然是物理学的重要组成部分。

2. 费米–狄拉克分布

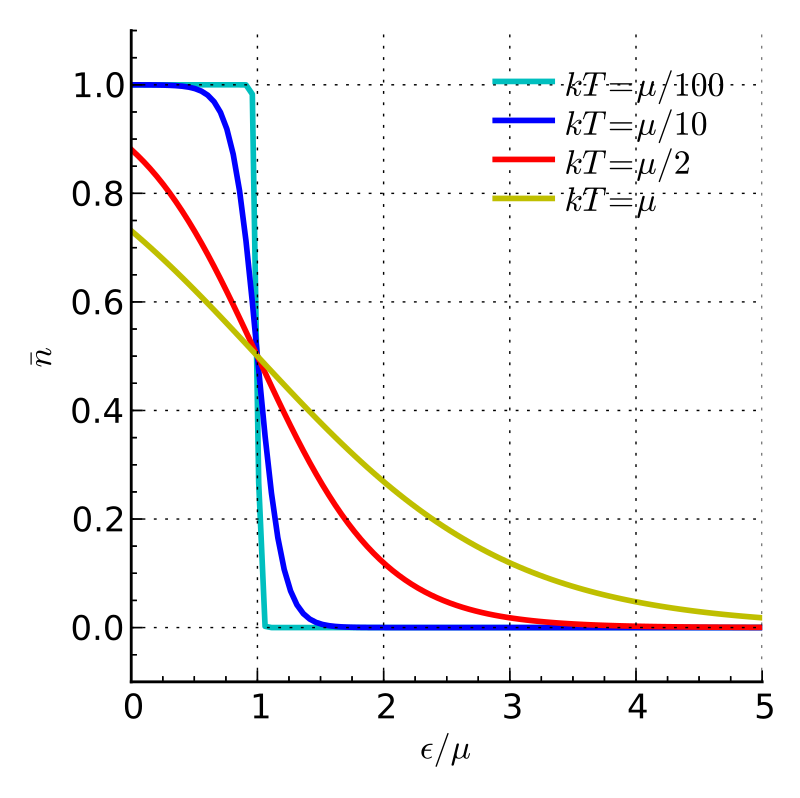
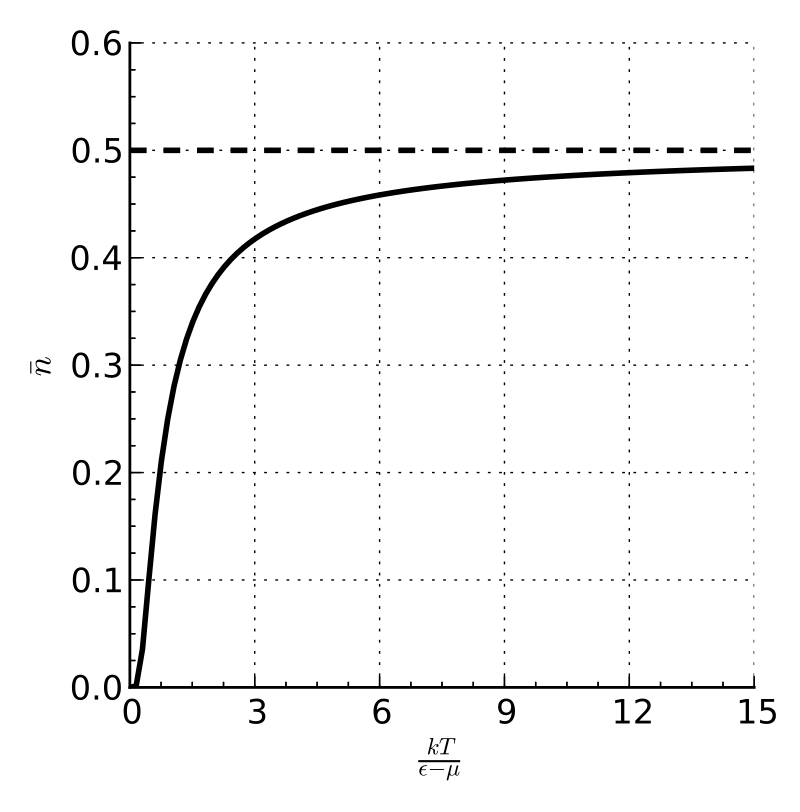
　　 对于一个由相同费米子组成并处于热力学平衡的系统，单粒子态 \( i \) 上的平均费米子数由费米–狄拉克(F–D)分布给出：\(^\text{[[11][nb 1]]}\) \[ \bar{n}_{i} = \frac{1}{e^{(\varepsilon_{i} - \mu)/k_{\text{B}}T} + 1}~ \] 其中 \(k_B\) 为玻尔兹曼常数，\(T\) 为绝对温度，\(\varepsilon_i\) 为 单粒子态 \(i\) 的能量，\(\mu\) 为总化学势。该分布由归一化条件 \[\sum_{i} \bar{n}_{i} = N~\] 约束，该条件可用于表示化学势 \(\mu\) 作为温度 \(T\) 和粒子数 \(N\) 的函数：\(\mu = \mu (T, N)\) 其中 \(\mu\) 可能取正值或负值。\(^\text{[12]}\)

　　 在绝对零温度下，化学势 \(\mu\) 等于费米能量加上每个费米子的势能，前提是该区域具有正的谱密度。在存在谱间隙（例如半导体中的电子）的情况下，对称点 \(\mu\) 通常被称为费米能级，对于电子而言，也被称为电化学势，它通常位于能隙的中心。\(^\text{[13][14]}\)

　　 费米–狄拉克分布仅在系统中的费米子数足够大的情况下才有效，这样额外添加一个费米子对化学势 \(\mu\) 的影响可忽略不计。[15] 由于费米–狄拉克分布的推导基于泡利不相容原理，该原理规定每个可能的量子态至多只能被一个费米子占据，因此分布函数的值始终满足 \(0 < \bar{n}_i < 1\)\(^\text{[nb 2]}\)

　　 状态 \(i\) 中粒子数的方差可以通过以下公式从 \(\bar{n}_i\) 的表达式计算得到：\(^\text{[17][18]}\) \[V(n_{i}) = k_{\text{B}}T \frac{\partial}{\partial \mu} \bar{n}_{i} = \bar{n}_{i} (1 - \bar{n}_{i}).~\]

粒子在能量上的分布

　　 从费米–狄拉克分布中，可以求出粒子在能量上的分布。\(^\text{[nb 3]}\) 具有能量 \( \varepsilon_i\) 的费米子的平均数目可以通过将费米–狄拉克分布 \(\bar{n}_i\) 与简并度 \(g_i\)（即具有能量 \(\varepsilon_i\) 的态的数目）相乘得到：\(^\text{[19]}\) \[ \bar{n}(\varepsilon_i) = g_i \bar{n}_i = \frac{g_i}{e^{(\varepsilon_i - \mu) / k_B T} + 1}.~ \] 当 \( g_i \geq 2 \) 时，可能会出现 \( \bar{n}(\varepsilon_i) > 1 \)，因为存在多个能量为 \( \varepsilon_i \) 的状态可以被费米子占据。

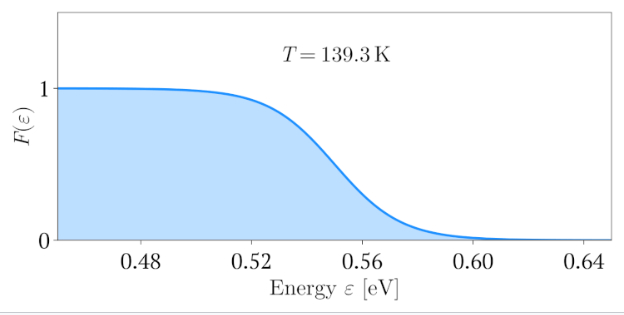
　　 当一个具有准连续能量 \(\varepsilon\) 的能量区间有一个相关的态密度 \( g(\varepsilon)\)（即单位能量范围单位体积内的状态数目）\(^\text{[20]}\)，则单位能量范围单位体积内的费米子平均数目为： \[ \bar{\mathcal{N}}(\varepsilon) = g(\varepsilon) F(\varepsilon),~ \] 其中 \(F(\varepsilon)\) 被称为费米函数，它与费米–狄拉克分布 \(\bar{n}_i\) 中使用的函数相同：\(^\text{[21]}\) \[ F(\varepsilon) = \frac{1}{e^{(\varepsilon - \mu) / k_B T} + 1},~ \] 因此： \[ \bar{\mathcal{N}}(\varepsilon) = \frac{g(\varepsilon)}{e^{(\varepsilon - \mu) / k_B T} + 1}.~ \]

3. 量子与经典范畴

　　 在高温和低粒子密度的极限下，费米–狄拉克分布趋近于麦克斯韦–玻尔兹曼分布，无需任何临时假设：

　　 在低粒子密度的极限下，\[\bar{n}_i = \frac{1}{e^{(\varepsilon_i - \mu) / k_B T} + 1} \ll 1,~\]因此，\(e^{(\varepsilon_i - \mu) / k_B T} + 1 \gg 1 \quad \text{或等效地} \quad e^{(\varepsilon_i - \mu) / k_B T} \gg 1\).在这种情况下，\[\bar{n}_i \approx \frac{1}{e^{(\varepsilon_i - \mu) / k_B T}} = \frac{N}{Z} e^{-\varepsilon_i / k_B T},~\]这就是麦克斯韦-玻尔兹曼统计的结果。

　　 在高温的极限下，粒子分布在一个较大的能量范围内，因此每个态的占据数（尤其是那些满足 \( \varepsilon_i - \mu \gg k_B T \) 的高能态）再次变得非常小，\[\bar{n}_i = \frac{1}{e^{(\varepsilon_i - \mu) / k_B T} + 1} \ll 1.~\]这再次简化为麦克斯韦-玻尔兹曼统计。

　　 经典范畴，即麦克斯韦–玻尔兹曼统计可以作为费米–狄拉克统计的近似，出现在远离海森堡不确定性原理对于粒子位置和动量的限制的情况。例如，在半导体物理学中，当导带的态密度远大于掺杂浓度时，可以使用麦克斯韦-玻尔兹曼统计来计算导带与费米能级之间的能隙。否则，如果掺杂浓度与导带的态密度相比不可忽略，则应使用费米–狄拉克分布来进行精确计算。可以进一步证明，当粒子浓度对应的平均粒子间距 \( \bar{R} \) 远大于粒子的平均德布罗意波长 \( \bar{\lambda} \) 时，经典情况占主导地位：\(^\text{[22]}\) \[ \bar{R} \gg \bar{\lambda} \approx \frac{h}{\sqrt{3mk_B T}},~ \] 其中 \( h \) 为普朗克常数，\( m \) 为粒子的质量。

　　 对于典型金属中导电电子的情况，在 \( T = 300 \, \text{K} \)（即大约室温）时，系统远离经典范畴，因为 \(\bar{R}\approx\bar{\lambda}/25\).这是由于电子的质量很小，以及金属中导电电子的高浓度（即小的 \( \bar{R} \)）。因此，对于典型金属中的导电电子，需要使用费米–狄拉克统计。\(^\text{[22]}\)

　　 另一个不属于经典范畴的系统示例是由已经塌缩为白矮星的恒星的电子组成的系统。尽管白矮星的温度很高（其表面典型温度为 \( T = 10000 \, \text{K} \)\(^\text{[23]}\)），但其高电子浓度和每个电子的质量很小，使得无法使用经典近似，因此同样需要使用费米–狄拉克统计。\(^\text{[8]}\)

4. 推导

大正则系综

　　 费米–狄拉克分布仅适用于非相互作用的费米子量子系统，可以通过大正则系综轻松推导得到。\(^\text{[24]}\) 在这个系综中，系统可以与热库进行能量和粒子的交换（热库通过温度 \(T\) 和化学势 \(\mu\) 来固定）。

　　 由于非相互作用的特性，每个可用的单粒子能级（具有能量 \( \varepsilon\)）形成一个与热库接触的独立热力学系统。换句话说，每个单粒子能级都是一个独立的小型大正则系综。根据泡利不相容原理，对于单粒子能级，只有两种可能的微观态：无粒子（能量 \(E = 0\)）或一个粒子（能量 \(E = \varepsilon\)）。因此，该单粒子能级的分配函数仅有两项： \[ \mathcal{Z} = \exp \left( 0 \cdot (\mu - \varepsilon) / k_B T \right) + \exp \left( 1 \cdot (\mu - \varepsilon) / k_B T \right) = 1 + \exp \left( =\mu - \varepsilon/k_B T \right),~ \] 该单粒子能级亚态的平均粒子数由下式给出： \[ \langle N \rangle = k_B T \frac{1}{\mathcal{Z}} \left( \frac{\partial \mathcal{Z}}{\partial \mu} \right)_{V,T} = \frac{1}{\exp \left( \varepsilon - \mu/k_B T \right) + 1}.~ \] 这个结果适用于每个单粒子能级，因此为整个系统的态给出了费米–狄拉克分布。\(^\text{[24]}\) 粒子数的方差（由于热波动）也可以推导出来（粒子数服从简单的伯努利分布）： \[ \langle (\Delta N)^2 \rangle = k_B T \left( \frac{d \langle N \rangle}{d \mu} \right)_{V,T} = \langle N \rangle (1 - \langle N \rangle).~ \] 这个量在输运现象中非常重要，例如莫特关系，它描述了电子气体的电导率和热电系数，\(^\text{[25]}\) 其中能级对输运现象的贡献能力与 \( \langle (\Delta N)^2 \rangle \) 成正比。

经典系综

　　 也可以在经典系综中推导费米–狄拉克统计。考虑一个由 \(N\) 个相同的费米子组成的多粒子系统，这些费米子之间的相互作用可以忽略不计，并且处于热平衡状态。\(^\text{[15]}\) 由于费米子之间的相互作用可以忽略，因此多粒子系统中状态 \(R\) 的能量 \(E_R\) 可以表示为单粒子能量的总和： \[ E_R = \sum_r n_r \varepsilon_r,~ \] 其中 \(n_r\) 称为占据数，表示具有能量 \(\varepsilon_r\) 的单粒子态 \(r\) 中的粒子数目。求和是对所有可能的单粒子态 \(r\) 进行的。

　　 多粒子系统处于状态 \(R\) 的概率由规范化的经典分布给出：\(^\text{[26]}\) \[ P_R = \frac{e^{-\beta E_R}}{\sum_{R'} e^{-\beta E_{R'}}},~ \] 其中 \(\beta = 1/k_B T\)，\( e^{-\beta E_R} \) 称为玻尔兹曼因子，求和是对多粒子系统的所有可能状态 \(R'\) 进行的。占据数 \(n_i\) 的平均值为：\(^\text{[26]}\) \[ \bar{n}_i = \sum_R n_i P_R.~ \] 注意，多粒子系统的状态 \(R\) 可以通过单粒子态的粒子占据数来指定，即通过指定 \( n_1, n_2, \ldots\) 来指定，因此 \[ P_R = P_{n_1, n_2, \ldots} = \frac{e^{-\beta (n_1 \varepsilon_1 + n_2 \varepsilon_2 + \cdots )}}{\sum_{n_1', n_2', \ldots} e^{-\beta (n_1' \varepsilon_1 + n_2' \varepsilon_2 + \cdots )}}~ \] 并且对于 \(\bar{n}_i\) 的方程变为 \[ \bar{n}_i = \sum_{n_1, n_2, \dots} n_i P_{n_1, n_2, \dots} = \frac{\sum_{n_1, n_2, \dots} n_i e^{-\beta (n_1 \varepsilon_1 + n_2 \varepsilon_2 + \cdots + n_i \varepsilon_i + \cdots )}}{\sum_{n_1, n_2, \dots} e^{-\beta (n_1 \varepsilon_1 + n_2 \varepsilon_2 + \cdots + n_i \varepsilon_i + \cdots )}}~ \] 其中求和是对所有符合泡利不相容原理的 \(n_1, n_2, \ldots\) 的值的组合进行的，并且对于每个 \( r \)，有 \( n_r = 0 \) 或 \( 1 \)。此外，每个 \( n_1, n_2, \ldots \) 的组合还满足总粒子数为 \(N\) 的约束： \[ \sum_r n_r = N~ \] 重新排列求和， \[ \bar{n}_i = \frac{\sum_{n_i=0}^{1} n_i e^{-\beta (n_i \varepsilon_i)} \sum_{n_1, n_2, \dots} e^{-\beta (n_1 \varepsilon_1 + n_2 \varepsilon_2 + \cdots )}}{\sum_{n_i=0}^{1} e^{-\beta (n_i \varepsilon_i)} \sum_{n_1, n_2, \dots} e^{-\beta (n_1 \varepsilon_1 + n_2 \varepsilon_2 + \cdots )}}~ \] 其中，求和符号上的上标 \( (i) \) 表示求和不包含 \( n_i \)，并且满足与求和相关的粒子总数约束 \( N_i = N - n_i \)。请注意，\( \sum^{(i)} \) 仍然通过 \( N_i \) 约束依赖于 \( n_i \)，因为在一种情况下 \( n_i = 0 \)，并且 \( \sum^{(i)} \) 是在 \( N_i = N \) 的条件下求值，而在另一种情况下 \( n_i = 1 \)，并且 \( \sum^{(i)} \) 是在 \( N_i = N - 1 \) 的条件下求值。为了简化符号并清晰地表示 \( \sum^{(i)} \) 仍然通过 \( N - n_i \) 依赖于 \( n_i \)，定义 \[ Z_i(N - n_i) \equiv \sum^{(i)}_{n_1, n_2, \dots} e^{-\beta (n_1 \varepsilon_1 + n_2 \varepsilon_2 + \cdots )}~ \] 这样，之前关于 \( \bar{n}_i \) 的表达式可以重新写成并用 \( Z_i \) 来求值： \[ \bar{n}_i = \frac{\sum_{n_i=0}^{1} n_i e^{-\beta (n_i \varepsilon_i)} Z_i(N - n_i)}{\sum_{n_i=0}^{1} e^{-\beta (n_i \varepsilon_i)} Z_i(N - n_i)}~ \] \[= \frac{0 + e^{-\beta \varepsilon_i} Z_i(N - 1)}{Z_i(N) + e^{-\beta \varepsilon_i} Z_i(N - 1)}~ \] \[ = \frac{1}{\left[Z_i(N)/Z_i(N - 1) \right] e^{\beta \varepsilon_i} + 1}.~ \] 以下近似 \(^\text{[27]}\) 将用于找到一个表达式来替代 \(Z_i(N)/Z_i(N-1)\)： \[ \ln Z_i(N-1) \simeq \ln Z_i(N) - \frac{\partial \ln Z_i(N)}{\partial N} = \ln Z_i(N) - \alpha_i,~ \] 其中 \[ \alpha_i \equiv \frac{\partial \ln Z_i(N)}{\partial N}.~ \] 如果粒子数 \(N\) 足够大，以至于当一个粒子被添加到系统中时，化学势 \(\mu\) 的变化非常小，那么 \(\alpha_i \simeq -\mu/k_B T\).\(^\text{[28]}\) 应用指数函数到两边，代入 \(\alpha_i\) 并重新排列， \[ Z_i(N)/Z_i(N-1)= e^{-\mu / k_B T}.~ \] 将上述代入 \( bar{n}_i\) 的方程，并使用先前定义的 \(\beta\) 来将 \(1/k_B T\) 替换为 \( \beta \)，得到费米–狄拉克分布： \[ \bar{n}_i = \frac{1}{e^{(\varepsilon_i - \mu)/k_B T} + 1}.~ \] 像麦克斯韦–玻尔兹曼分布和玻色–爱因斯坦分布一样，费米–狄拉克分布也可以通过达尔文–福勒的均值法推导出来。\(^\text{[29]}\)

　　 例如，将两个粒子分配到三个子能级中，将得到人口数为 110、101 或 011 的三种方式，总共为 3 种方式，计算结果为 \(3!/2!1!\)。

　　 一组占据数 \( n_i \) 可以实现的方式数是每个单独能级可以被占据的方式数的乘积： \[ W = \prod_i w(n_i, g_i) = \prod_i \frac{g_i!}{n_i!(g_i - n_i)!}.~ \] 遵循与推导麦克斯韦–玻尔兹曼统计相同的过程，我们希望找到一组 \( n_i \)，使得 \( W \) 最大化，同时满足粒子数和总能量固定的约束。我们使用拉格朗日乘子法来约束我们的解，形成以下函数： \[ f(n_i) = \ln W + \alpha (N - \sum n_i) + \beta (E - \sum n_i \varepsilon_i).~ \] 使用斯特林近似法对阶乘进行近似，分别对 \( n_i \) 求导，将结果设为零，并解出 \( n_i \)，最终得到费米–狄拉克人口数： \[ n_i = \frac{g_i}{e^{\alpha + \beta \varepsilon_i} + 1}.~ \] 通过类似于麦克斯韦–玻尔兹曼统计中所述的过程，可以从热力学角度证明，\( \beta = \frac{1}{k_B T} \) 且 \( \alpha = -\frac{\mu}{k_B T} \)，因此，最终某个状态被占据的概率为： \[ \bar{n}_i = \frac{n_i}{g_i} = \frac{1}{e^{(\varepsilon_i - \mu)/k_B T} + 1}.~ \]

5. 另见

• 大正则系综
• 泡利不相容原理
• 完全费米–狄拉克积分
• 费米能级
• 费米气体
• 麦克斯韦–玻尔兹曼统计
• 玻色–爱因斯坦统计
• 旁统计
• 逻辑函数
• S 型函数

6. 注释

1. 费米–狄拉克分布是一种数学函数，称为逻辑函数或 S 型函数。
2. 请注意，\( \bar{n}_i \) 也是状态 \( i \) 被占据的概率，因为同一个状态在同一时间内最多只能被一个费米子占据，并且 \( 0 < \bar{n}_i < 1 \)。
3. 这些关于能量的分布，有时也称为费米–狄拉克分布，但本文中不会使用该术语

　　 。

7. 参考文献

1. 费米，恩里科（1926）。"Sulla quantizzazione del gas perfetto monoatomico"。Rendiconti Lincei（意大利语）。3: 145–9，翻译为 Zannoni，Alberto（1999-12-14）。"On the Quantization of the Monoatomic Ideal Gas"。arXiv:cond-mat/9912229.
2. 狄拉克，保罗·A·M（1926）。"On the Theory of Quantum Mechanics"。《皇家学会 A 类会议录》。112（762）：661–77。Bibcode:1926RSPSA.112..661D。doi:10.1098/rspa.1926.0133。JSTOR 94692。
3. （Kittel 1971，第 249–250 页）
4. "History of Science: The Puzzle of the Bohr–Heisenberg Copenhagen Meeting"。Science-Week。4（20）。2000-05-19。OCLC 43626035。2009-04-11 存档。检索于 2009-01-20。
5. Schücking（1999）。"Jordan, Pauli, Politics, Brecht and a variable gravitational constant"。Physics Today。52（10）：26。Bibcode:1999PhT....52j..26S。doi:10.1063/1.882858。
6. Ehlers; Schücking（2002）。"Aber Jordan war der Erste"。Physik Journal（德语）。1（11）：71–72。hdl:11858/00-001M-0000-0013-5513-D。
7. 狄拉克，保罗·A·M（1967）。《量子力学原理》（修订版第 4 版）。伦敦：牛津大学出版社。第 210–211 页。ISBN 978-0-19-852011-5。
8. 福勒，拉尔夫·H（1926 年 12 月）。"On dense matter"。《皇家天文学会月刊》。87（2）：114–22。Bibcode:1926MNRAS..87..114F。doi:10.1093/mnras/87.2.114。
9. 索默费尔德，阿诺德（1927 年 10 月 14 日）。"Zur Elektronentheorie der Metalle" [金属的电子理论]。Naturwissenschaften（德语）。15（41）：824–32。Bibcode:1927NW.....15..825S。doi:10.1007/BF01505083。S2CID 39403393。
10. 福勒，拉尔夫·H；诺德海姆，洛塔尔·W（1928 年 5 月 1 日）。"Electron Emission in Intense Electric Fields"。《皇家学会 A 类会议录》。119（781）：173–81。Bibcode:1928RSPSA.119..173F。doi:10.1098/rspa.1928.0091。JSTOR 95023。
11. Reif 1965，第 341 页。
12. 兰道，L.D.，利夫希茨，E.M.（2013）。《统计物理：第 5 卷》（第 5 卷）。Elsevier。
13. Blakemore 2002，第 11 页。
14. Kittel, Charles; Kroemer, Herbert（1980）。《热物理学》（第 2 版）。旧金山：W. H. Freeman。第 357 页。ISBN 978-0-7167-1088-2。
15. Reif 1965，第 340–342 页。
16. Kittel 1971，第 245 页，图 4 和图 5。
17. Pearsall, Thomas（2020）。《量子光子学，第 2 版》。物理学研究生教材。Springer。doi:10.1007/978-3-030-47325-9。ISBN 978-3-030-47324-2。
18. （Reif 1965，第 351 页）公式 9.7.7，其中 \( \beta = \frac{1}{k_B T} \)，\( \alpha = -\frac{\mu}{k_B T} \)，\( \frac{\partial \bar{n}_i}{\partial \epsilon_i} = -\frac{\partial \bar{n}_i}{\partial \mu} \)。
19. Leighton, Robert B.（1959）。《现代物理学原理》。McGraw-Hill。第 340 页。ISBN 978-0-07-037130-9。请注意，在公式（1）中，\( n(\varepsilon) \) 和 \( n_s \) 分别对应本文中的 \( \bar{n}_i \) 和 \( \bar{n}(\varepsilon_i) \)。另见第 339 页公式（32）。
20. Blakemore 2002，第 8 页。
21. Reif 1965，第 389 页。 （Reif 1965，第 246–248 页）
22. Mukai, Koji; Jim Lochner（1997）。"Ask an Astrophysicist"。NASA 的《想象宇宙》。NASA 戈达德航天中心。2009-01-18 存档。
23. Srivastava, R. K.; Ashok, J.（2005）。"第 6 章"。《统计力学》。新德里：PHI Learning Pvt. Ltd. ISBN 9788120327825。
24. Cutler, M.; Mott, N.（1969）。"Observation of Anderson Localization in an Electron Gas"。《物理评论》。181（3）：1336。
25. Bibcode:1969PhRv..181.1336C。doi:10.1103/PhysRev.181.1336。
26. Reif 1965，第 203–206 页。
27. 例如，参见导数 § 通过差商定义，它给出了近似公式 \( f(a + h) \approx f(a) + f'(a)h \)。
28. Reif 1965，第 341–342 页。参见公式 9.3.17 和关于近似有效性的备注。
29. Müller-Kirsten, H. J. W.（2013）。《统计物理学基础》（第 2 版）。世界科学出版社。ISBN 978-981-4449-53-3。
30. Blakemore 2002，第 343–534 页。

8. 进一步阅读

1. Reif, F.（1965）。《统计与热物理基础》。McGraw–Hill。ISBN 978-0-07-051800-1。
2. Blakemore, J. S.（2002）。《半导体统计》。Dover。ISBN 978-0-486-49502-6。
3. Kittel, Charles（1971）。《固体物理学导论》（第 4 版）。纽约：John Wiley & Sons。ISBN 978-0-471-14286-7。OCLC 300039591。