差分

贡献者： 有机物; addis

　　 差分算法可以很快速的给一段区间 $[l, r]$ 加上一个数 $c$。

　　 一维差分

　　 朴素的做法和前缀和类似，都是直接一个 for 循坏给区间中的每个数都加 $c$，朴素做法的时间复杂度为 $\mathcal{O}(n \times m)$，$n$ 为序列大小，$m$ 为询问次数。

　　 差分做法是，构造一个差分数组 $b$，使得 $b_i = a_i - a_{i - 1}$，$(i \geq 2)$，特殊的，规定 $b_1 = a_1$。因此 $a$ 数组就是 $b$ 数组的前缀和，$b$ 数组就称是 $a$ 数组的差分数组。 $$\begin{cases} b_1 = a_1 \\ b_2 = a_2 - a_1 \\ b_3 = a_3 - a_2 \\ \cdots \\ b_i = a_i - a_{i - 1} \end{cases}~,$$

　　 若要对 $[l, r]$ 中的每个数加 $c$，对应在 $a$ 数组就是 $c\sum^r_{i= l}a_i$。可以直接在 $b$ 数组上对 $b_l$ 这个位置加 $c$，那么在求 $a$ 数组时，$a_l$、$a_{l + 1}$、$a_{l + 2}$ $\cdots$ $a_n$ 都会加上 $c$。因为 $a$ 数组就是 $b$ 数组的前缀和。

　　 例子：假设要对 $[1, n]$ 每个数都加 $c$，那么只需要将 $b_1$ 加 $c$ 即可。可见 $a_{1 ... n}$ 都加了 $c$。

　　 $\begin{cases} a_1 = a_0 + b_1 \\ a_2 = a_1 + b_2 \\ \cdots \\ a_n = a_{n - 1} + b_n \end{cases}$

　　 因为只需要在 $[l, r]$ 中的每个数加 $c$，$a_{r + 1 ... n}$ 这些数是不需要加的，我们只需要对应在 $b_{r + 1}$ 减去 $c$ 就行了。对应在 $a$ 数组就是 $a_{r + 1..n}$ 这些数没有任何变化。

const int N = 1e5 + 10;
int n, m, a[N], b[N];

int main() 
{
    cin >> n >> m;  
    for (int i = 1; i <= n; i ++ ) cin >> a[i];
    for (int i = 1; i <= n; i ++ ) b[i] = a[i] - a[i - 1]; // 构造差分数组

    while (m -- ) // m 次询问
    {
        int l, r, c;
        cin >> l >> r >> c;
        b[l] += c, b[r + 1] -= c;   // O(1) 计算
    }
    
    for (int i = 1; i <= n; i ++ ) 
    {
        a[i] = a[i - 1] + b[i]; // 求一遍前缀和
        cout << a[i] << ' ';   
    }
    
    return 0;
}

　　 另外一种构造方式：

void insert(int l, int r, int c)
{
    b[l] += c;
    b[r + 1] -= c;
}

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) 
    {
        cin >> a[i];
        insert(i, i, a[i]);
    }
    
    while (m -- )
    {
        int l, r, c;
        cin >> l >> r >> c;
        insert(l, r, c);
    }
    
    for (int i = 1; i <= n; i ++ ) 
    {
        a[i] = a[i - 1] + b[i];
        cout << a[i] << ' ';
    }
    
    return 0;
}

　　 上面两种写法是等价的。

　　 下面介绍二维差分：

　　 二维差分是将一个矩阵内部以 $(x_1, y_1)$ 左上角、$(x_2, y_2)$ 为右下角的子矩阵内部的每个元素都加 $c$。

　　 朴素做法类似于一维差分，时间复杂度为 $\mathcal{O}(q \times n^2)$，$q$ 为询问次数，$n^2$ 为子矩阵大小。

　　 二维差分也同样是构造一个二维差分数组，使得二维数组 $a$ 是 $b$ 数组的二维前缀和。怎么构造差分数组可以不用考虑，只需要考虑核心操作，然后对矩阵中的每个数做一遍核心操作即可构造好 $b$ 数组。可以直接在 $b$ 数组上进行如下几个操作：

1. $b_{x_1, y_1}$ 加 $c$
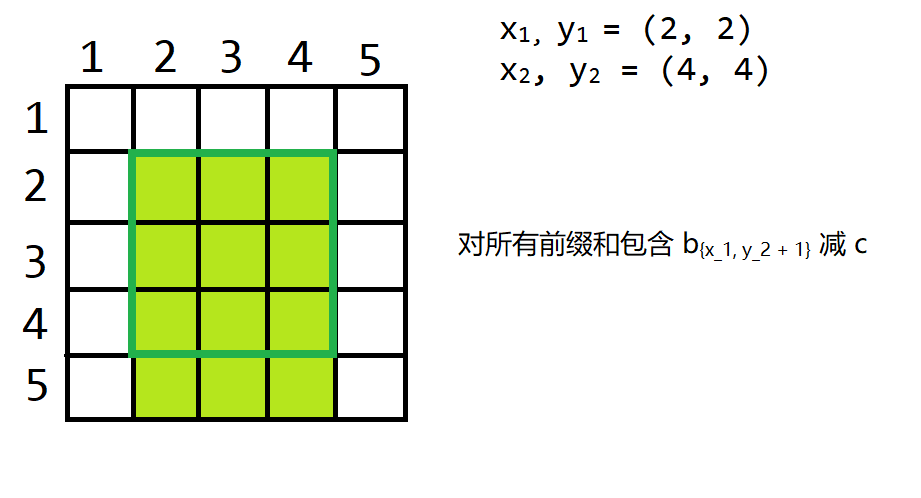
2. $b_{x_1, y_2 + 1}$ 减 $c$
3. $b_{x_2 + 1, y1}$ 减 $c$
4. $b_{x_2 + 1, y_2 + 1}$ 加 $c$

　　 执行完以上 $4$ 个操作，再对 $b$ 数组求一遍前缀和。就可以得到期望答案。

　　 具体来讲：(都会求前缀和)执行完操作 $1$ 后，以 $x_1, y_1$ 为左上角的矩阵都被加了 $c$。执行完操作 $2$ 后，以 $x_1, y_2 + 1$ 为左上角的矩阵都被减了 $c$。执行完操作 $3$ 后，以 $x_2 + 1, y1$ 为左上角的矩阵都被减了 $c$。执行完操作 $4$ 后，以 $x_2 + 1, y_2 + 1$ 为左上角的矩阵都被加了 $c$。

　　 二维差分还是比较抽象，可以根据几张图来理解：

const int N = 1100;
int n, m, q, a[N][N], b[N][N];

void insert(int x1, int y1, int x2, int y2, int c)
{
    b[x1][y1] += c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y1] -= c;
    b[x2 + 1][y2 + 1] += c;
}

int main()
{
    cin >> n >> m >> q;
    for (int i = 1; i <= n; i ++ ) 
        for (int j = 1; j <= m; j ++ )
        {
            cin >> a[i][j];
            insert(i, j, i, j, a[i][j]);   // 构造差分数组 b
        }
        
    while (q -- )
    {
        int x1, y1, x2, y2, c;
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        insert(x1, y1, x2, y2, c);
    }
    
    for (int i = 1; i <= n; i ++ ) 
    {
        for (int j = 1; j <= m; j ++ )
        {
            // 求 a 数组，就是求 b 的二维前缀和
            a[i][j] = a[i - 1][j] + a[i][j - 1] 
                    - a[i - 1][j - 1] + b[i][j];    
            cout << a[i][j] << ' ';
        }
        cout << endl;
    }

    return 0;
}