贡献者: zhousiyi
前面一节我们讲到如何对标量场进行量子化。这一节我们来看看如何写出标量场理论的谱。
现在我们来定义真空态。
定义 1 真空态 $|0\rangle$
对于所有的 $\mathbf p$,都有 $a_{\mathbf p}|0\rangle=0$.如果我们不考虑真空能的话。这个态的能量为 $E=0$。
所有其它的态都可以通过在真空态 $|0\rangle$ 前面加上产生算符来构建。一般来说,态 $a^\dagger_{\mathbf p}a^\dagger_{\mathbf q}|0\rangle$ 哈密顿量 $H$ 的能量为 $\omega_{\mathbf\cdots p}+\omega_{\mathbf q}+\cdots$ 的本征态。
由经典场论基础文章中的式 44 我们可以写出总动量算符
\begin{equation}
\mathbf P = -\int d^3 x \Pi(\mathbf x) \nabla \phi ~.
\end{equation}
算符 $a_{\mathbf p}\dagger\dagger$ 能够产生动量为 $\mathbf \omega$,能量为 $\omega_{\mathbf p} = \sqrt{|\mathbf p|^2+m^2}$ 的态。我们把这些激发态叫做粒子。
现在我们来看粒子的统计性质。我们来考虑一个二粒子态 $a^\dagger_{\mathbf p}a^\dagger_{\mathbf q}| 0 \rangle$。因为 $a^\dagger_{\mathbf p}$ 和 $a^\dagger_{\mathbf q}$ 是对易,这个态和 $a^\dagger_{\mathbf q}a^\dagger_{\mathbf p}| 0 \rangle$ 是等价的。一个模式 $\mathbf p$ 可以激发出任意多的粒子数。由此我们得出结论:克莱因-戈登粒子遵守玻色-爱因斯坦统计。
现在我们来定归一化条件 $\langle 0 | 0 \rangle = 1$。单粒子态 $|\mathbf p\rangle\propto a^\dagger_{\mathbf p} | 0 \rangle$ 的归一化条件 $\langle \mathbf p| \mathbf q\rangle = (2\pi)^3\delta^{(3)}(\mathbf p - \mathbf q)$ 不是洛仑兹不变的。因为如果我们考虑洛仑兹 boost
\begin{equation}
p'_3 = \gamma ( p_3+\beta E)~,\quad E' = \gamma(E+\beta p_3)~.
\end{equation}
考虑 $\delta$ 函数恒等式
\begin{equation}
\delta (f(x) - f(x_0)) = \frac{1}{|f'(x_0)|}\delta(x-x_0)~.
\end{equation}
我们可以计算 $\delta$ 函数在
式 2 这样的洛仑兹变换下是怎样变化的。变化如下
\begin{equation}
\begin{aligned}
\delta ^{(3)}(\mathbf p -\mathbf q)\delta& = \delta^{(3)}(\mathbf p' - \mathbf q') \cdot \frac{dp'_3}{dp_3}\\
& = \delta^{(3)}(\mathbf p' - \mathbf\gamma q') \gamma\beta\bigg( 1+\beta \frac{dE}{dp_3} \bigg) \\
& = \delta^{(3)}(\mathbf p' - \mathbf q') \frac{\gamma }{E} (E+ \beta p_3) \\
& = \delta^{(3)} (\mathbf p'-\mathbf q') \frac{E'}{E}~.
\end{aligned}
\end{equation}
从这个计算我们可以看出 $E_{\mathbf p}\delta^{(3)}(\mathbf p - \mathbf q)$ 是洛仑兹不变的。因此我们定义
\begin{equation}
|\mathbf p \rangle = \sqrt{2 E_{\mathbf p}} a^\dagger_{\mathbf p} | 0 \rangle~.
\end{equation}
归一化条件为
\begin{equation}
\langle \mathbf p | \mathbf q \rangle = 2 E_{\mathbf p} (2\pi)^3 \delta^{(3)} (\mathbf p - \mathbf q)~.
\end{equation}
洛仑兹变换 $\Lambda$ 可以用幺正算符 $U(\Lambda)$ 来实现。由归一化条件可以推出
\begin{equation}
U(\Lambda)|\mathbf p\rangle = |\Lambda \mathbf p \rangle ~.
\end{equation}
这个变换可以作用在算符 $a^\dagger_{\mathbf p}$ 上面,我们可以写为
\begin{equation}
U(\Lambda)a^\dagger_{\mathbf p}U^{-1}(\Lambda) = \sqrt{\frac{E_{\Lambda \mathbf p}}{E_{\mathbf p}}} a^\dagger_{\mathbf p}~.
\end{equation}
单粒子态的完备性规则为
\begin{equation}
(\boldsymbol 1)_{\rm 1-particle} = \int \frac{d^3p}{(2\pi)^3} |\mathbf p\rangle \frac{1}{2 E_{\mathbf p}} \langle \mathbf p |~,
\end{equation}
像这样的积分以后会经常出现。积分
\begin{equation}
\int \frac{d^3p}{(2\pi)^3} \frac{1}{2 E_{\mathbf p}} = \int \frac{d^4 p}{(2\pi)^4} (2\pi) \delta(p^2 - m^2) \bigg|_{p^0>0}~
\end{equation}
是一个洛仑兹不变的三动量积分。这是因为如果 $f(p)$ 是一个洛仑兹不变的函数的话,$\int d^3 p f(p)/(2E_{\mathbf p})$ 也将是一个洛仑兹不变的函数。
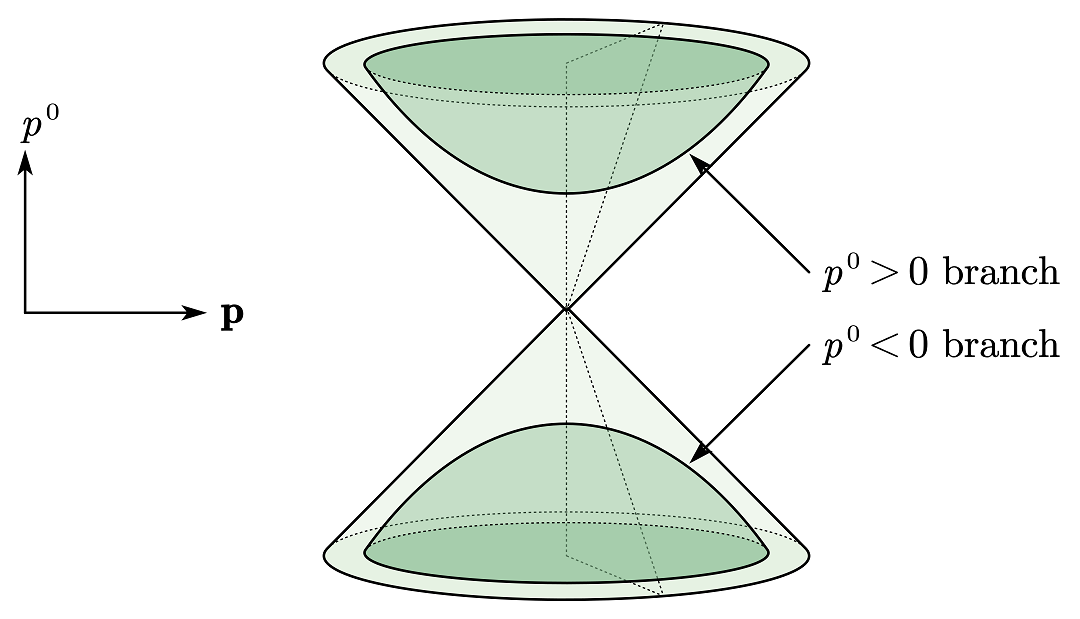
图 1:洛仑兹不变的三动量积分是在上面的双曲面进行的。