sinc 函数
贡献者: addis
$ \operatorname{sinc} $ 函数的定义为
\begin{equation}
\operatorname{sinc} x =
\left\{\begin{aligned}
&\frac{\sin x}{x} &\quad & (x \ne 0)\\
&\quad 1 && (x = 0)
\end{aligned}\right. ~.\end{equation}
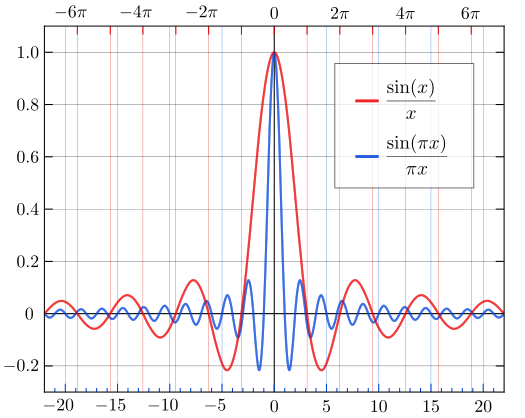
$ \operatorname{sinc} $ 函数的图像如图 1 ,可以证明,该函数在 $x=0$ 处是连续的,即
\begin{equation}
\lim_{x \to 0}\frac{\sin x}{x} = \operatorname{sinc} 0 = 1~.
\end{equation}
图 1:sinc 函数(来自维基百科)
积分性质
\begin{equation}
\int_{-\infty}^{+\infty} \operatorname{sinc} x \,\mathrm{d}{x} = \pi~,
\end{equation}
证明见例 1 。
\begin{equation}
\int_{-\infty}^{+\infty} \operatorname{sinc} ^2 x \,\mathrm{d}{x} = \pi~.
\end{equation}
$ \operatorname{sinc} $ 函数的原函数称为正弦积分函数,详见 “三角积分”。