循环群

                     

贡献者： 叶月2_

　　 显然，循环群的群元都可以表示为生成元的整数次幂，因此循环群实际上是阿贝尔群。由群的封闭性可知，给定群 $G$ 的一个群元素 $g$，那么 $ \left\langle g \right\rangle \subset G$。

　　 循环群的形式看似没有什么规律，但我们可以借助同构来缩减研究对象。

　　 proof.¹

　　 设 $G$ 是无限循环群，建立 $\mathbb Z\rightarrow G$ 的同态映射，使得对于任意 $n\in \mathbb Z$，都有 $f(n)=a^n$。根据群同态基本定理习题 2 ，我们有 $\mathbb Z/ \operatorname {ker}f\cong G$。由于 $\mathbb Z$ 的正规子群都是 $n\mathbb Z,n\in \mathbb N$，因此模 $n$ 同余类与 $G$ 同构。当该 $n=0$ 时，对应无限循环群；当 $m\neq 0$ 时，$\mathbb Z_n$ 与 n 元循环群同构。

　　 因为有限循环群可以继承整数群的乘法，因此还是一个环。可以证明，$\mathbb Z_n$ 环上的零因子是 $n$ 的因子。所以，如果 $n$ 是素数，那么这个环就是无零因子交换幺环了，我们一般简称其为整环。

　　 只要证明任意环元都有逆在环内即可。 因为是有限整环，假设生成元为 $a$，则由封闭性知对于每个非零同余类都必有 $a^m=a^n,m\neq n$。设 $m n$，因为 $a^{m-n}a^n=1\cdot a^n$，所以 $a^{m-n}=1$²。因此，$a^{m-n-1}$ 为 $a$ 的逆元，$a^{k(m-n-1)}$ 是 $a^k$ 的逆元，证毕。

1. 循环群的子群结构

　　 proof. 设循环群 $G= \left\langle a \right\rangle $，则其子群元素必定包含 $a$ 的某次幂。设任意子群为 $G_1$ 包含元素的最小次幂为 $k$，则该子群包含 $a^{kn},n\in \mathbb Z$。若该群不是循环群，必然包含元素形如 $a^{kn+r}$，其中 $0< r< k$。由封闭性知也包含 $a^{-kn}=(a^{kn})^{-1}$。则 $a^{r}\in G^{1}$，与假设里 $k$ 是最小正整数矛盾，所以循环群的子群必是循环群。

　　 proof.

　　 因为 $a^{\frac{n}{d}d}=e$，因此 $ \left\langle a \right\rangle ^{\frac{n}{d}}$ 是一个 $d$ 阶子群。下面证明唯一性。

　　 设 $H=\{x\in G|x^d=e\}$，易证这是 $G$ 的子群且具有唯一性。又设 $x=a^k$，则 $a^{kd}=e$ 意味着 $n|kd$，则 $\frac{n}{d}|k$。因为 $G$ 是 $n$ 阶子群，所以 $k$ 的可能取值范围为 $\{1,2...n\}$，也即 $\{\frac{n}{d},2\frac{n}{d}...d\frac{n}{d}\}$。所以 $H$ 的阶小于或等于 $d$。

　　 又因为 $a^{\frac{n}{d}}\in H$，则 $ \left\langle a \right\rangle ^{\frac{n}{d}}\subset H$，所以 $H$ 的阶必等于 $d$ 且 $H= \left\langle a \right\rangle ^{\frac{n}{d}}$。 换句话说，循环群的不同子群阶数不同。实际上，其逆命题也是成立的。即 $G$ 是循环群 $\Longleftrightarrow G$ 的不同子群阶数不同。

　　 proof.³

　　 设 $H$ 为 $G$ 的任意子群，因为共轭子群的阶与原群相等，即对于任意 $g\in G$ 都有 $|gHg^{-1}|=|H|$，题设条件使得 $G$ 的任意子群都是正规子群——$H\lhd G$。设 $G'=G/H$ 且 $H_1$ 是 $G'$ 的任意子群，那么对于 $G$ 而言，$H_1$ 是运算封闭的左陪集之并，也就是说，$H_1$ 也是原群的子群，题设及 “任意子群都是正规子群” 在商群意义上得以继承。

　　 因此，我们可以利用循环子群来构造商群列。从 $G$ 里选任意元素 $x_1$，构造商群 $G_1=G/ \left\langle x \right\rangle _1$，从 $G_1$ 中选任意元素 $x_2$，构造商群 $G_2=G_1/ \left\langle x \right\rangle _2$，以此类推——

我们知道，根据拉格朗日定理，商群的基数必是原群基数的因子，因此商群列总是有限的，最后终结于平凡群。又因为该平凡群是 $G_{s-1}$ 商去循环群得到的，所以 $G_{s-1}$ 必是循环群。

　　 接下来我们只需要证明，对于 $G_{n}=G_{n-1}/ \left\langle x \right\rangle _n$，若满足 $G_{n}$ 为循环群，则 $G_{n-1}$ 也必是循环群即可。这其实是从商群列逆向推导出 $G$ 是循环群。

　　 设 $r$ 是 $G_n$ 的生成元代表元素，即 $r \left\langle x \right\rangle _n$ 生成了这个循环群。设 $|G_{n}|=d$，则对于任意 $r_1,r_2\in r \left\langle x \right\rangle _n$ 都有 $r_1^d,r_2^d\in \left\langle x \right\rangle _n$。$r_1\rightarrow r_1^d$ 是从左陪集 $r \left\langle x \right\rangle _n$ 到正规子群 $ \left\langle x \right\rangle _n$ 的映射，下面证明这是一个双射。

　　 设 $r_1\neq r_2$，且 $r_1^d=r_2^d$。在 $G_{n-1}$ 中，$ \left\langle r \right\rangle _1$ 和 $ \left\langle r \right\rangle _2$ 是两个阶数相同，但元素不同的子群，与题设矛盾。所以 $r_1\rightarrow r_1^d$ 是单射。又因为正规子群和陪集的基数相同，所以该映射既单又满。

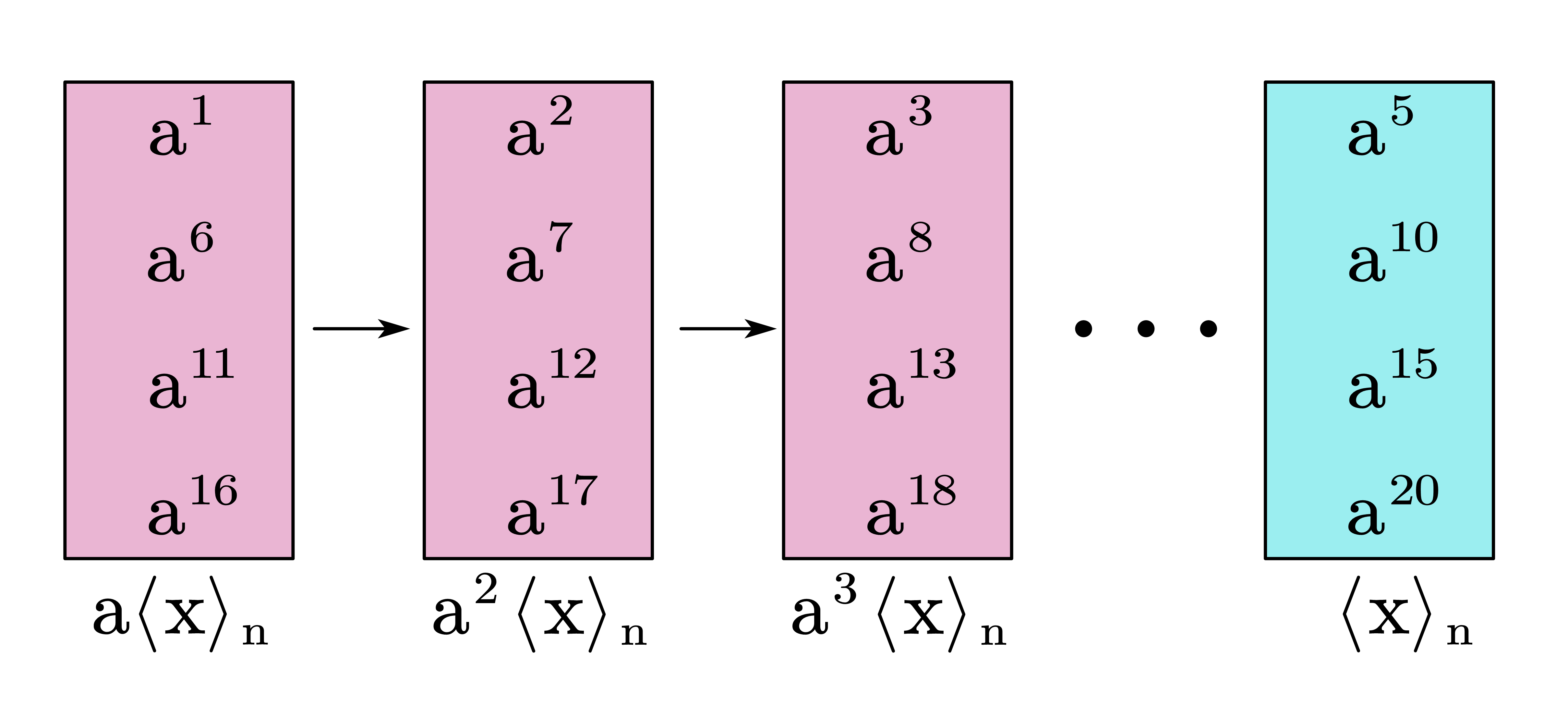
　　 因此在 $r \left\langle x \right\rangle _n$ 中存在唯一的 $a$ 使得 $a^d=x$，把陪集表示为 $a^i \left\langle a^d \right\rangle ,i=1,2...d$，则 $G_{n-1}$ 确实是一个循环群，证毕。

　　 取 $d=5$，上述的 $G_{n-1}$ 及其陪集划分如下图所示。

---

1. ^ 参考《抽象代数》，邓少强祝，朱富海著。
2. ^ 注意这是环上的乘法，由于乘法运算构成半群，消去律未必成立。若对于环上元素有 $ab=cb$ 且 $b\neq 0$，则 $(a-c)b=0$。由于整环没有零因子，所以 $a=c$，即消去律对整环必然成立。
3. ^ 引自《代数学基础》，Jier Peter 著。