（低阶）偏微分方程的分类与特征线

贡献者： int256; addis

预备知识　偏导数（数学分析），常微分方程，矩阵的本征问题

　　对于低阶偏微分方程而言，我们可以找到一族曲线，偏微分方程的初值信息沿着这条曲线传播（体现为在这条曲线上值不变或衰减），这条曲线就被称为特征线，而由于解沿这曲线传递，我们就可以通过解常微分方程的方法求出这条曲线（将在下面的例子中看到这一点）。最直白的说，就是偏微分方程这个系统随时间的演化，沿着特征线将变为 “常微分方程”。

　　我们可以假想初值是一物理系统的初始状态，从初值情况开始，解将进行传播并产生波，描述这个 “波” 传递的过程就是特征线法，故又称行波法。

　　同时，特征线法为二阶 PDE 提供了一个分类方法。

　　本文默认 PDE 的范围是 $-\infty < x, y, \dots < +\infty, t>0$，用 $u'_t$ 表示 $ \frac{\partial u}{\partial t} $，用 $u'_x$ 表示 $ \frac{\partial u}{\partial x} $。默认二阶导连续，即 $u''_{xy} = u''_{yx} = \frac{\partial }{\partial y} \left( \frac{\partial u}{\partial x} \right) = \frac{\partial }{\partial x} \left( \frac{\partial u}{\partial y} \right)$。

　　特征线有如下性质，

对于 $n$ 维（这里包含时间维）的 PDE，其特征线总是 $n-1$ 维的。
解的 “间断” 性质通过、且仅能通过特征线传播。（也就是说，不同时刻，同一特征线上的解相同，但有时数值会沿特征线衰减。）
特征线上 PDE 的解是一样的（或衰减），特征线的斜率是解 “传播” 的速度。

　　其中性质 $2$ 对应着如果不存在特征线（特征线不是实的，类似一元二次方程没有实数根称为根不存在），那么 PDE 的解连续（这就是 elliptic PDE）。

　　同时求出特征线还有助于解决诸如影响区域、依赖区域一类的问题（这是由解信息沿特征线传播决定的）。

1. 特征线

　　考虑一个一阶拟线性方程的柯西问题，一般形式为

\begin{equation}\left\{ \begin{aligned} & a(x, t, u) u_x + b(x, t, u)u_y = c(x, t, u), ~ -\infty < x < +\infty, t > 0 \\ & u(x, 0) = \varphi(x), -\infty < x < +\infty ~~ \end{aligned}\right. ~. \end{equation}

　　这有一个直观的几何解释：在 $(x, t, u)$ 的三维空间中，曲面上任意一点 $P_0(x_0, t_0, u_0)$ 的法向量为 $\vec n=(u_x, u_t, -1) |_{P_0}$。在曲面 $u = u(x, t)$ 上，曲线

\begin{equation} \Gamma: x=x(s), t=t(s), u=u(x(s), t(s)) ~~ \end{equation}

在点 $P_0$ 处的切向量为

\begin{equation} \vec \tau = \left.\left( \frac{\mathrm{d}{x}}{\mathrm{d}{s}} , \frac{\mathrm{d}{t}}{\mathrm{d}{s}} , \frac{\mathrm{d}{u}}{\mathrm{d}{s}} \right) \right|_{P_0} ~. \end{equation}

显然，$\vec n$ 与 $\vec \tau$ 在 $P_0$ 互相垂直。

　　当考虑矢量 $\vec \mu = (a(x, t, u), b(x, t, u), c(x, t, u))|_{P_0}$，则微分方程恰好表示法向量 $\vec n$ 与 $\vec \mu$ 在 $P_0$ 点处互相垂直，从而在曲面 $u = u(x, t)$ 上以 $\vec \mu$ 为切矢量且与曲线 $\Gamma$ 相交，交点是 $(\alpha, 0, \varphi(\alpha))$ 的曲线方程为：

\begin{equation}\left\{ \begin{aligned} \frac{\mathrm{d}{x}}{\mathrm{d}{s}} &= a(x, t, u), ~ x(0) = \alpha \\ \frac{\mathrm{d}{t}}{\mathrm{d}{s}} &= b(x, t,u), ~ t(0) = 0 \\ \frac{\mathrm{d}{u}}{\mathrm{d}{s}} &= c(x, t, u), ~ u(0) = \varphi(\alpha) ~ \end{aligned}\right. ~~ \end{equation}

　　其中 $\alpha$ 是曲线的参数，这组微分方程的解就被称为特征线。这条曲线在 $(x, t)$ 平面的投影就是一般意义的特征线，给出原微分方程的解曲面。

2. 一维一阶 PDE

　　特征线法为一维一阶 PDE 提供了一个解法：先求出特征线，后代入求出初值在特征线上的传播情况即可。

定理 1　

　　对于关于 $u(x, t)$ 的一维一阶 PDE：

\begin{equation} \frac{\partial u}{\partial t} + A(x, t) \frac{\partial u}{\partial x} + B(x, t) u = f(x, t) ~, \end{equation}

初值条件 $u(x, 0) = \phi(x), -\infty < x < +\infty$。

　　设特征线族为 $x = x(t, \tau)$，由 $\tau$ 决定是 “哪根” 特征线（对应初值）。

　　由于初值沿着特征线传播，则 $x = x(t, \tau)$ 应是下面 ODE 的解，

\begin{equation} \left\{ \begin{aligned} \frac{\mathrm{d}{x}}{\mathrm{d}{t}} &= A(x, t), \\ x(0) &= \tau ~. \end{aligned} \right . \end{equation}

考虑 $v(t) = u(x(t), t)$，由全微分与偏导的关系， $$ \frac{\mathrm{d}{v}}{\mathrm{d}{t}} = \frac{\partial u}{\partial x} \frac{\mathrm{d}{x}}{\mathrm{d}{t}} + \frac{\partial u}{\partial t} \frac{\mathrm{d}{t}}{\mathrm{d}{t}} = \frac{\partial u}{\partial x} \cdot A(x, t) + \frac{\partial u}{\partial t} ~,$$ 这便是特征线的解。若再要求解原方程组，又有：

\begin{equation} \left\{ \begin{aligned} \frac{\mathrm{d}{v}}{\mathrm{d}{t}} + B(x, t) v &= f(x(t), t) ~, \\ v(0) = u(x(0), 0) &= u(\tau, 0) = \phi(x) ~. \end{aligned} \right. \end{equation}

　　下面利用两个一维一阶的 PDE 举例来说明如何求解 PDE 的特征线。

例 1　

　　求解这 PDE 的特征曲线：

\begin{equation} \left \{ \begin{aligned} u'_t + (x + t) u'_x + u &= x ~, \\ \left. u \right\rvert _{t=0} &= x ~. \end{aligned} \right . \end{equation}

　　解：特征曲线 $x=x(t)$ 对应下面 ODE，

\begin{equation} \left \{ \begin{aligned} \frac{\mathrm{d}{x}}{\mathrm{d}{t}} &= x+t ~, \\ x(0) &= \tau ~. \end{aligned} \right . \end{equation}

可以解得 $x(t) = e^t - t - 1 + \tau \cdot e^t$。

　　另一个方法则是考虑特征线下的坐标系 $(s, \tau)$，其中 $\tau$ 仍是某个常数，由选择的 “哪条” 特征线而定，而 $s \ge 0$ 是代表在某条特征线上的位置。

图 1：$s-\tau$ 坐标系 [1]

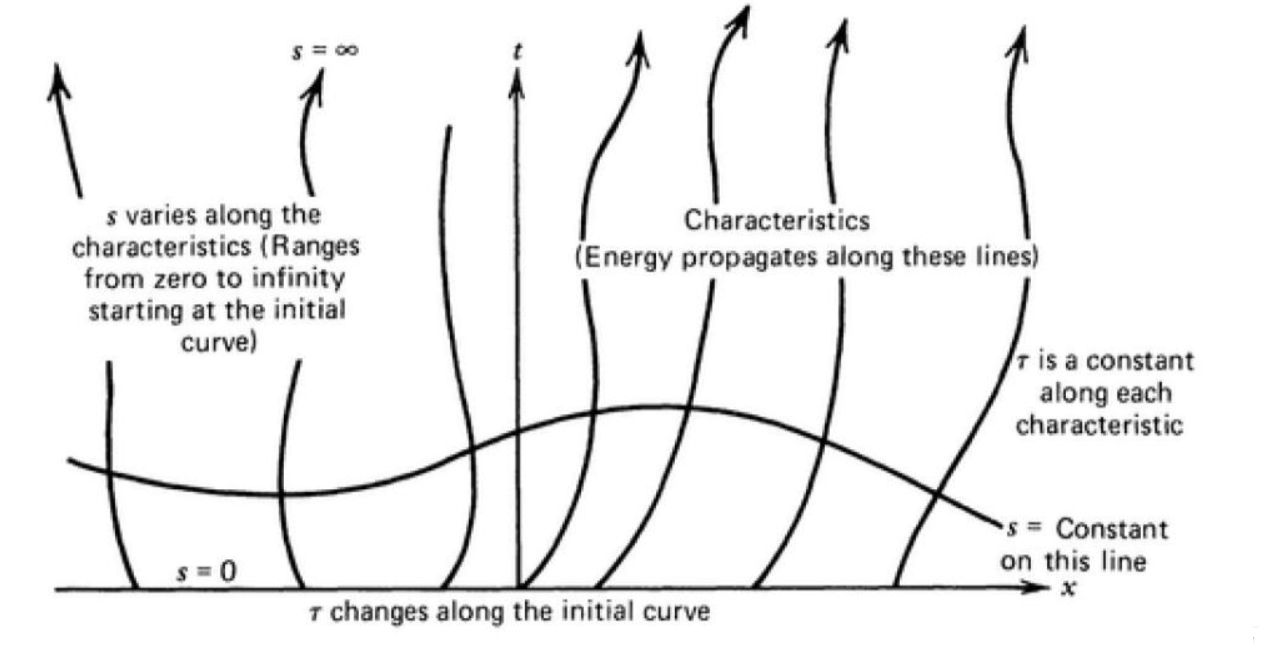
例 2　

　　通过特征线法求这 pde 的解： $$ \left\{ \begin{aligned} {u_t'} + {u_x'} &= -u, -\infty < x < +\infty, t > 0, \\ u(x, 0) &= \sin x, -\infty < x < +\infty . \end{aligned} \right. ~~ $$

　　解：考虑将原 PDE 转化到 $s-\tau$ 坐标系下的 ODE。由全微分与偏微分的关系： $$ \frac{\mathrm{d}{u}}{\mathrm{d}{s}} = \frac{\partial u}{\partial x} \frac{\mathrm{d}{x}}{\mathrm{d}{s}} + \frac{\partial u}{\partial t} \frac{\mathrm{d}{t}}{\mathrm{d}{s}} ~, $$ 则由 $u_t' + u_x' = -u$，因而 $u_t' + u_x' + u = 0$，就有 $$ \frac{\mathrm{d}{u}}{\mathrm{d}{s}} + u = \frac{\partial u}{\partial x} \frac{\mathrm{d}{x}}{\mathrm{d}{s}} + \frac{\partial u}{\partial t} \frac{\mathrm{d}{t}}{\mathrm{d}{s}} + u = 0 ~.$$ 对比系数，得到特征线方程： $$ \frac{\mathrm{d}{x}}{\mathrm{d}{s}} = 1, \frac{\mathrm{d}{t}}{\mathrm{d}{s}} = 1~, s>0$$ 故 $x(s) = s+C_1, t(s) = s+C_2$。

　　令 $s=0$，得到 $x(0) = C_1, t(0) = C_2$。结合 $s-\tau$ 坐标系的意义，$x(0)$ 是由 $\tau$ 决定的初值 $x(0) = \tau$，$t(0)=0$。故 $x(s) = s+\tau, t(s)=s$。则特征线方程就是 $x = t+\tau$。

　　下面利用上面求出的特征线将原 pde 转化为 ode 求解： $$ \left\{ \begin{aligned} \frac{\mathrm{d}{u}}{\mathrm{d}{s}} +u &= 0, s>0, \\ \left. u \right\rvert _{s=0} &= u( \left. x \right\rvert _{s=0}, \left. t \right\rvert _{s=0}) = u(\tau, 0) = \sin \tau . \end{aligned} \right.~~$$ 故 $u(s,\tau) = \exp\left(-s\right) \sin \tau$。

　　下面将 $u(s, \tau)$ 转化回到 $x-t$ 坐标系下： $x(s) = s + \tau, t(s) = s$，故 $u(x, t) = \exp\left(-t\right) \sin\left(x-t\right) $。

图 2：解的示意

　　可以发现解沿着特征线有衰减的传播。图中画出了 $0\le t\le3$, $0\le x \le 4 \pi$ 的情况。

　　同时，对于二元二阶线性的 PDE，其特征线是 2 维的，并且我们将会看到其体现出圆锥曲线的性质，同时各类圆锥曲线的特征线对应的 PDE 有不同的性质。下面我们来讨论特征线与 PDE 的分类。

3. 二阶线性 PDE 的分类

　　在一般的数理方程或介绍 PDE 的书籍中，会把二阶线性 PDE 将之主要分为以下三类，分别是

椭圆类（elliptic PDE），例如泊松方程 $ \boldsymbol{\nabla}^2 u = f$；
抛物类（parabolic PDE），例如热传导方程 $k \boldsymbol{\nabla}^2 T = \frac{\partial T}{\partial t}$；
双曲类（hyperbolic PDE），例如波动方程 $ \boldsymbol{\nabla}^2 w = \frac{1}{c^2} \frac{\partial^2 w}{\partial t^2}$。

　　这三类的解信息沿特征线传播，有性质与对应的物理问题：

椭圆类：解的信息以无限速度传播，且解不应当存在间断。适用于平衡问题（静态或准静态，例如无源力场）。
抛物类：解的信息以无限速度传播，适用于扩散问题（例如热传导）。
双曲类：解的信息以有限速度传播，且能保留间断信息，适用于波动问题。

　　另外还有一类 PDE 被称为 ultrahyperbolic PDE（超双曲类）。下面将讲解是如何分类的。

二元二阶线性 PDE

　　首先保持二阶导连续的假设，即 $ \frac{\partial }{\partial x} \frac{\partial u}{\partial y} = \frac{\partial }{\partial y} \frac{\partial u}{\partial x} $。则偏微分方程具有一般形式： $$Au''_{xx} + Bu''_{xy} + Cu''_{yy} + Du'_{x} + Eu'_{y} + F = 0 ~,$$ 与一阶线性 PDE 对比，可以得到特征线应当满足方程： $$ \left\{ \begin{aligned} \,\mathrm{d}{(u'_{x})} &= u''_{xx} \,\mathrm{d}{x} + u''_{xy} \,\mathrm{d}{y} ,\\ \,\mathrm{d}{(u'_{y})} &= u''_{xy} \,\mathrm{d}{x} + u''_{yy} \,\mathrm{d}{y} . \end{aligned} \right. ~~$$ 联立这三式，令有三个矩阵：

\begin{equation} \boldsymbol{\mathbf{M}} = \begin{pmatrix} A & B & C \\ \,\mathrm{d}{x} & \,\mathrm{d}{y} & 0 \\ 0 & \,\mathrm{d}{x} & \,\mathrm{d}{y} \end{pmatrix}, \boldsymbol{\mathbf{p}} = \begin{pmatrix} u''_{xx} \\ u''_{xy} \\ u''_{yy} \end{pmatrix}, \boldsymbol{\mathbf{N}} = \begin{pmatrix} -D u'_{x} - E u'_{y} - F\\ \,\mathrm{d}{(u'_{x})} \\ \,\mathrm{d}{(u'_{y})} \end{pmatrix} ~~ \end{equation}

则这三式可转化为 $ \boldsymbol{\mathbf{Mp}} = \boldsymbol{\mathbf{N}} $。显然，$u$ 的各个二阶偏导项不是唯一确定的，所以 $\det \boldsymbol{\mathbf{M}} = 0$，也就是需要：

\begin{equation} A\left(\mathrm{d} y\right)^2 - B\left(\mathrm{d} x \mathrm{d} y\right) + C\left(\mathrm{d} x\right)^2 =0 ~, \end{equation}

也就是：

\begin{equation} A\left( \frac{\mathrm{d}{y}}{\mathrm{d}{x}} \right)^2 - B\left( \frac{\mathrm{d}{y}}{\mathrm{d}{x}} \right) + C = 0 ~, \end{equation}

发现是一个关于 $ \,\mathrm{d}{y} / \,\mathrm{d}{x} $ 的二次方程，判别式 $\Delta = B^2-4AC$。对比一般利用二次表达式的圆锥曲线定义，可以将特征线分类如下。

$\Delta < 0$，存在虚特征线（即无特征线），称这种为椭圆类 PDE；
$\Delta = 0$，存在一族特征线，称这种为抛物类 PDE；
$\Delta > 0$，存在两族不同的特征线，称这种为双曲类 PDE。

　　这就是分类的依据。

　　值得注意的是，PDE 可能在不同区域有不同分类。例如 $y u''_{xx} - u''_{yy} = 0$，在 $y> 0$ 时是双曲类；在 $y=0$ 时是抛物类，在 $y<0$ 时是椭圆类。

多元二阶线性 PDE

　　考虑线性微分算符 $\hat L$：

\begin{equation} \hat L u = \sum_{i, j}\left( \boldsymbol{\mathbf{A}} _{i, j} \cdot \frac{\partial }{\partial x_i} \left( \frac{\partial u}{\partial x_j} \right)\right) + \sum_{i}\left( \boldsymbol{\mathbf{B}} _{i} \frac{\partial u}{\partial x_i} \right) + F~, \end{equation}

忽略低阶项（一阶的 $ \boldsymbol{\mathbf{B}} _{i}$ 与 $F$），考虑系数矩阵 $ \boldsymbol{\mathbf{A}} _{i,j}$ 的特征值，我们将 $\hat Lu=0$ 分类如下。

当特征值均大于 $0$ 或均小于 $0$，即特征值全部同号且都非零，归类为椭圆类；
当特征值有一个为 $0$，其余均大于 $0$ 或均小于 $0$，即特征值除有一 $0$ 外均同号，归类为抛物类；
当特征值一个为正数，其他为负数；或一个为负数，其他为正数。即特征值均非 $0$，并且有仅有一非 $0$ 特征值与其他非 $0$ 特征值符号相反，归类为双曲类；
正特征值和负特征值的个数都均大于一，且特征值均非 $0$，归类为超双曲类。

　　一般来说，对于一个有物理意义的 PDE，特征值有一个为 $0$ 的归类为抛物类，其余全同号为椭圆类，否则大概率为双曲类。

[1] ^ Stanley J. Farlow, Partial Differential Equations for Scientists and Engineers. 1993.