分离性

                     

贡献者： JierPeter

预备知识　紧致性

1. 分离性的种类一览

　　 分离性是描述一个拓扑空间里，任意的点、子集等彼此之间能被不相交的开集分开的程度。我会在这里先列出常见的分离性和它们的简单解释，但你不需要掌握所有分离性，只有其中两个是很重要的。

定义 1　分离性的种类

　　

  • $T_0$ 分离性，是指取空间中不同的两点 $x,y$，总存在一个开集 $U$，使得 $U$ 包含其中一点而不包含另一点。
  • $T_1$ 分离性，是指取空间中不同的两点 $x,y$，总存在两个开集分别含有其中一个点，但各自不含有另一个点。
  • $T_2$ 分离性，是指取空间中不同的两点 $x,y$，总存在两个开集，分别含有其中一个点，并且这两个开集不相交。
  • $T_3$ 分离性，是指取空间中不同的两点 $x,y$ 或者将 $y$ 替换为一个不含 $x$ 的闭集，那么总存在两个开集，分别含有其中一个点或闭集，并且这两个开集不相交。
  • 正规分离性，是指取空间中不相交的两个闭集 $A, B$，总存在两个开集，分别含有其中一个闭集，并且这两个开集不相交。
  • $T_4$ 分离性，是指既正规分离又 $T_2$ 分离的性质。

　　 这些分离性之间的区别很细微，看起来很绕，对不对？数学家们将分离性的分类做得比这个要详细得多，除了列表里的，他们还研究了诸如 $T_{2.5}$ 分离性，$T_{3.5}$ 分离性，$R_1$ 分离性，完全正规分离性，正则分离性，正则 Hausdorff 分离性等非常多的分离性。但常用的重要分离性只有其中两个，$T_2$ 分离性和正规分离性。其中 $T_2$ 分离性又被称为 Hausdorff 分离性。

习题 1　度量空间是 Hausdorff 的

　　 给定度量空间中不同的两点 $x, y$，构造出两个开集 $U_x$ 和 $U_y$，使得 $x\in U_x$，$y\in U_y$，但 $U_x\cap U_y=\varnothing$。

推论 1　

　　 由习题 1 可推知，度量空间必然是 Hausdorff 空间。

2. Hausdorff 空间和正规空间

　　 为了方便读者，无须在定义 1 里翻找，我将重新誊写一遍两个重要分离性的定义。

定义 2　Hausdorff 空间和正规空间

　　 给定拓扑空间 $X$。

  • 称 $X$ 是 Hausdorff 空间，如果任意的 $x,y\in X$，都可以被两个不相交的开集 $U_x, U_y$ 分别包含。
  • 称 $X$ 是正规空间，如果任意的两个闭集$A, B\subseteq X$，都可以被两个不相交的开集 $U_A, U_B$ 分别包含。

　　 我们在紧致性一节的开头提到，紧子集的行为常常和单个点是相似的，而紧子集又常常是闭集；在这里，Hausdorff 空间和正规空间的概念差别，无非就是一个讨论点和点的关系，另一个讨论闭集和闭集的关系。它们也因此有一些类似的性质。

定理 1　分离性的继承

　　 Hausdorff 空间的任意子空间还是 Hausdorff 的。正规空间的任意闭子空间还是正规的。

　　 定理证明是很简单的。注意正规空间的继承性要求必须是闭子集构成的空间，因为只有这样才能保证子空间的闭集仍然是原来空间的闭集，从而直接继承原空间的分离性。举个反例，线段 $[0,10]$ 上的度量空间是正规的，如果取子集 $(1,3)\cup(4,5)$ 来构成子空间，那么根据子拓扑的定义 3 ，$[2,4]\cap[(1,3)\cup(4,5)]=[2,3)$ 是 $(1,3)\cup(4,5)$ 空间的闭集，但它显然不是 $[0,10]$ 空间的闭集。当然了，$(1,3)\cup(4,5)$ 空间也不是正规空间。

　　 紧的 Hausdorff 空间有一个非常良好的性质：它的紧子集和闭集是等价的。

定理 2　紧 Hausdorff 空间的性质

  • 紧 Hausdorff 空间的紧子集一定是闭的。
  • 紧 Hausdorff 空间是正规空间。

　　 这个定理的证明是非常巧妙的，我列举如下，感兴趣的读者可以仔细体会：

　　 证明：

　　 要证明一个集合是闭集，等价于证明它的补集是开集。

　　 取拓扑空间 $X$。设 $A$ 是 $X$ 的紧子集，任取 $x\in X-A$。

　　 取 $A$ 中任意一点 $a$，由 Hausdorff 分离性，存在两个开集 $U_a\ni a, V_a\ni x$，并且 $U_a$ 和 $V_a$ 不相交。对每一个 $a\in A$ 都取出这样的 $U_a$，$V_a$ 对，那么 $\{U_a\}_{a\text{取遍}A}$ 是 $A$ 的一个覆盖。由于 $A$ 是紧子集，这个覆盖存在有限子覆盖。

　　 也就是说，存在有限个 $a_i\in A, i=1, 2, \cdots n$，使得 $\{U_{a_i}\}$ 就足以覆盖 $A$ 了。这里的有限非常关键，因为它使得 $\bigcap\limits_{i=1,2, \cdots n}V_{a_i}$ 是开集的有限交，因此仍然是开集1。

　　 记 $\bigcup\limits_{i=1,2, \cdots n}V_{a_i}=U$，且 $\bigcap\limits_{i=1,2, \cdots n}V_{a_i}=V$，则 $U, V$ 都是开集，$U\supseteq A$，$V\ni x$，并且 $U, V$ 没有交集 $\rightarrow A, V$ 没有交集。

　　 因此，$x$ 是 $X-A$ 的一个内点。由于 $x$ 是任意取的，故可知每一个 $x\in X-A$ 都是其内点，故 $X-A$ 是开集，故 $A$ 是闭集。

　　 类似地可以对两个不相交的闭集中的点彼此配对，应用 Hausdorff 分离性和 Hausdorff 空间中闭集等价于紧集，可以类似地证明紧 Hausdorff 空间都是正规空间。

　　 证毕。

3. 一点紧化空间

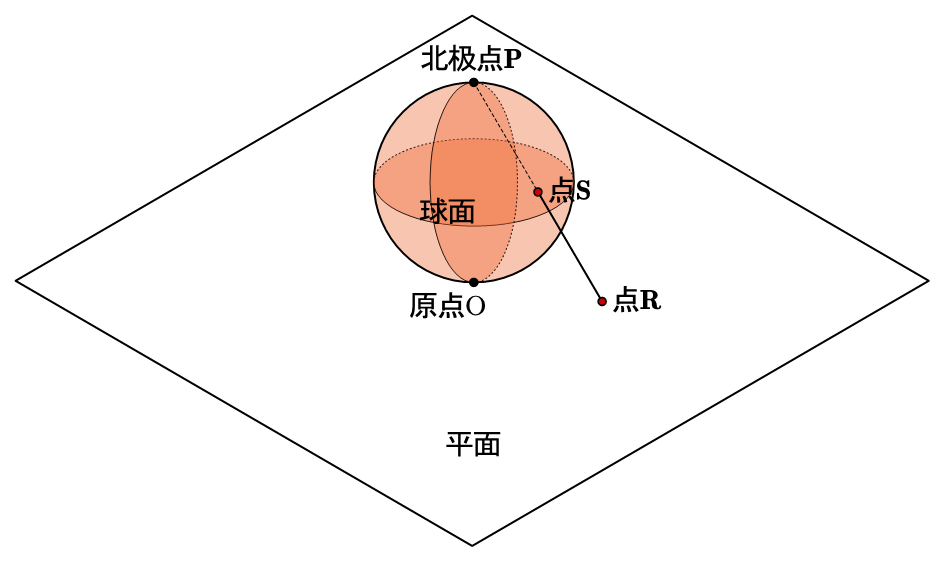
　　 Hausdorff 空间不一定是紧空间，但是总可以添上一个点以后成为紧空间。最常见的例子就是二维平面添上一个点以后成为一个球面，原本的二维平面因为无穷延伸，所以不是紧空间；但是添上一点再相应定义一些新的开集以后，它就等价于一个有限的球面了，从而变成了紧空间。这种添上一点使非紧空间变成紧空间的操作，叫做 “一点紧化”。

　　 假设有一个 Hausdorff 空间 $(X, \mathcal{T})$，它不紧致。我给它添上一个点，叫做无穷远点，记为 $P$，得到一个新的集合 $X\cup \{\mathcal{P}\}=X'$，在这个集合 $X'$ 上定义拓扑：开集一共分两种，含 $P$ 和不含 $P$ 的。不含 $P$ 的开集都是原先 $X$ 中的开集，而含 $P$ 的开集 $O$，都是某个 $K\subseteq X$ 的补集：$O=X'-K$。其中 $K$ 是 $X$ 的一个紧集。这样构成了一个新的空间 $(X', \mathcal{T}')$，称为 $(X, \mathcal{T})$ 的一点紧化空间。

　　 这样添上一个点并加入和含这个点的开集的定义，就能得到一个紧 Hausdorff 空间。二维平面变成球面的过程就是这样的。

例 1　黎曼球面

　　

　　 平面几何所研究的空间 $\mathbb{R}^2$ 是一个 Hausdorff 空间，但它不紧致——这是很显然的，如果你取 $A_n$ 是以原点为圆心、$n$ 为半径的圆盘，那么 $\{A_n\}$ 自然是整个平面的一个覆盖，而它不存在有限子覆盖。当我们给这个平面添加一个无穷远点 $P$ 并按照上述方式进行一点紧化以后，所得到的空间实际上等价于一个球面，记为 $S^2$。

　　 反过来，你也可以把 $\mathbb{R}^2$ 平面看成是球面 $S^2$ 挖去了一个点 $P$ 构成的。事实上，如果你把一个球放在这个平面的原点处，让球的南极点和原点重合，然后从球的北极点拉出一条条射线穿过球面和平面，球面上和平面上被穿过的点相互联系，就几乎构成了球面和平面的一个双射，几乎每一个球面上的点都唯一对应平面上的一个点，除了北极点本身。这个北极点就是我们所讨论的 $P$ 点，那个在平面上并不存在的无穷远点。

图
图 1：黎曼球面示意图。图中球面的南极点和平面的原点 $O$ 是重合的。从北极点 $P$ 拉出的一条射线在 $S$ 穿过球面，和平面相交于 $R$。球面和平面上的各点 $S$ 和 $R$ 以这种方式一一对应。

　　 这样给 $\mathbb{R}^2$ 平面添上一个无穷远点并定义新的开集以后所得到的球面，被称为黎曼球面。通常我们会规定这个球面半径为 $1$。

1. ^ 回顾拓扑的定义，只要求了任意并和有限交的封闭性；以 $\mathbb{R}$ 为例也可看出，对于所有正整数 $n$，开区间 $(-1,1/n)$ 的交集是 $(-1, 0]$，这显然不是一个开集。

                     

© 小时科技 保留一切权利