潮汐力

贡献者： ACertainUser; addis

本文处于草稿阶段。
本文需要更多参考文献。

预备知识　万有引力、引力势能，离心力

图 1：潮汐力分布示意图（地球参考系）

　　我们先以月球对地球的潮汐力为例，并忽略地球自转、公转等因素。

图 2：月球对地球各点的引力不同

　　众所周知，引力与两点距离有关： $$ \boldsymbol{\mathbf{F}} _\text{引力}= - \frac{GMm}{R^2}\hat R~.$$

　　如图 2 所示，由于月球到地球各点的距离不同，所以准确的说，月球对地球各点的引力也不同，而潮汐现象正是由于引力的这种细微差异。地球表面上正对月球 $A$ 点、背对月球的 $B$ 点的引力分别为：

\begin{equation} \begin{aligned} \boldsymbol{\mathbf{F}} _A &= - \frac{GM_\text{月}\Delta m}{(R-r)^2} \hat R~,\\ \boldsymbol{\mathbf{F}} _B &= -\frac{GM_\text{月} \Delta m}{(R+r)^2}\hat R~.\\ \end{aligned} \end{equation}

图 3：地球与月球正相互环绕

　　同时别忘了，地球与月球正相互环绕，因此地球整体还有向心加速度

\begin{equation} \boldsymbol{\mathbf{a}} _\text{地球} = -\frac{GM_\text{月}}{R^2}\hat R~. \end{equation}

以上二式中，$r$ 是地球半径，$R$ 是地月距离，$\hat R$ 是从月球指向地球的单位方向向量，负号表示引力方向是从地球指向月球的。

图 4：地球表面上，正对与背对月球的两点都被拉起

　　如图 4 所示，从地球这一非惯性参考系上看，地球整体有加速度意味着各点都还受一个离心力(不是地球自转的离心惯性力，而是地球与月球转动的)： $$f_\text{惯} = - \boldsymbol{\mathbf{a}} _\text{地球} \Delta m =\frac{GM_\text{月}\Delta m}{R^2}\hat R~.$$考虑到这个因素后，有趣的事情发生了：在一个地球人看来，地球表面上正对与背对月球的两点似乎都正被拉起，这就是潮汐力。某种意义上，潮汐力也是由于处于地球这一非惯性参考系的我们的错觉。

　　具体而言，A 点处的潮汐力为 $$ \boldsymbol{\mathbf{F}} _A' = \boldsymbol{\mathbf{F}} _A - a_\text{地球}\Delta m = -\frac{GM_\text{月}\Delta m}{(R-r)^2}\hat R + \frac{GM_\text{月}\Delta m}{R^2} \hat R \approx -\frac{2rGM_\text{月}\Delta m}{R^3} \hat R~. $$ 同理，B 点处的潮汐力为 $$ \boldsymbol{\mathbf{F}} _B' = \boldsymbol{\mathbf{F}} _B - a_\text{地球}\Delta m \approx \frac{2rGM_\text{月}\Delta m}{R^3} \hat R~. $$

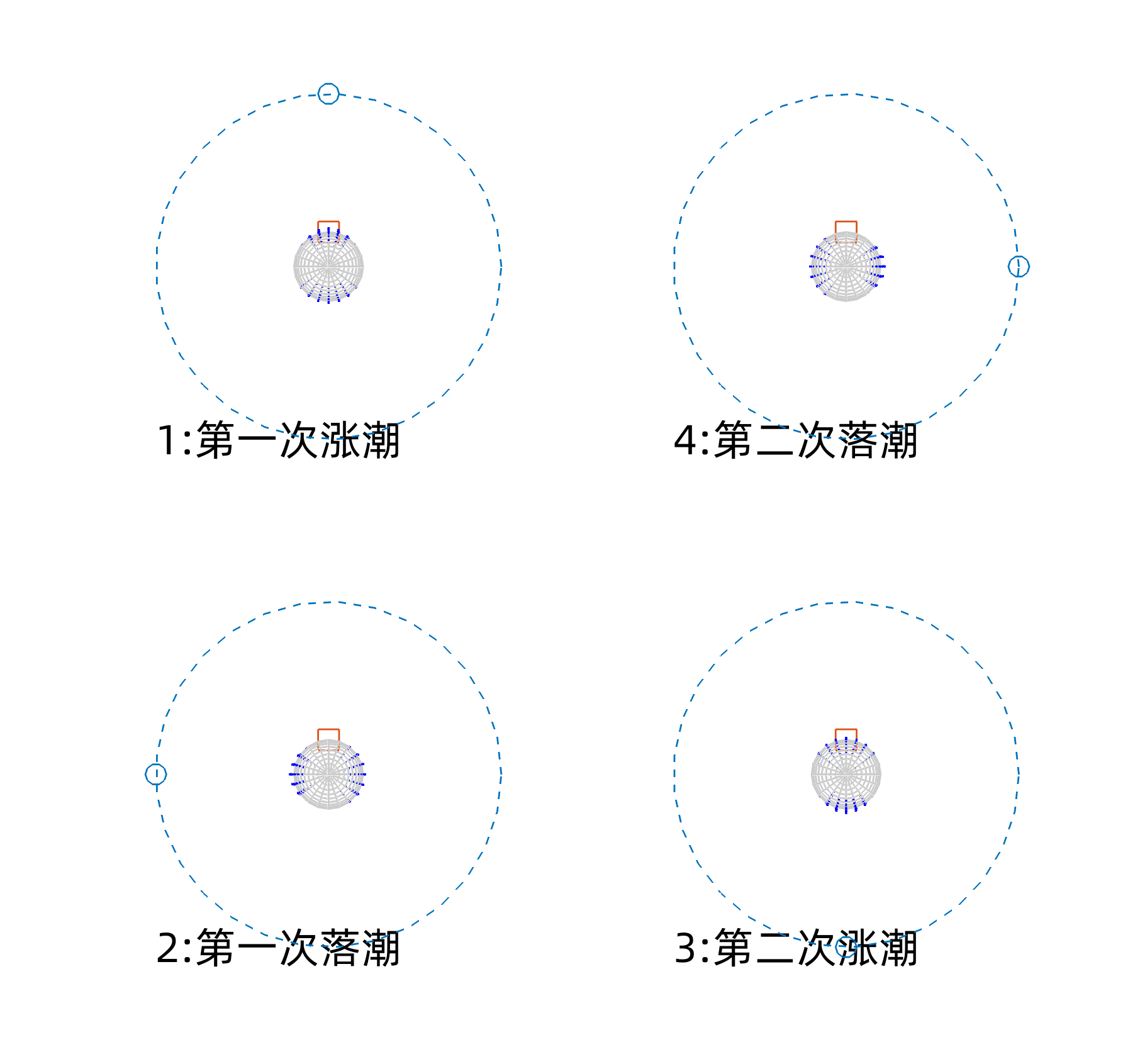
　　从图 4 可以发现，无论是正对月球的一面，还是背对月球的一面，潮汐力的方向都是离开地表的。因此，潮汐力不能简单地理解为 “因为地球的一面离月球更近，所以那一侧的海洋被吸起了”。由于潮汐力的这一非同寻常的性质（再加上之前被忽略的地球自转），因此一天之内，地球出现两次潮汐现象。

图 5：一天内，地球出现两次潮汐现象

　　同时，我们发现潮汐力是与距离的三次方成反比的，这意味着感性上说 “潮汐力比引力衰减得更快”。

习题 1　谁是弄潮儿？

　　你可能觉得太阳的质量远比月球大，因此太阳对地球产生的潮汐作用更明显？是这样的吗？¹

　　绘制地球表面潮汐力分布的 Matlab 代码：

clc
clear

[x y z] = sphere(20);
xs = -60; %地月距离大概是地球半径的60倍
scatter3(xs,0,0);

u = x - xs;
v = y;
w = z;

r = sqrt(u.^2+v.^2+w.^2);
mag = 10^4./(r.^2);

u = -mag.*u./r;
v = -mag.*v./r;
w = -mag.*w./r;
u = u + 10^4/(xs^2); %地球参考系这一非惯性参考系中的离心力。注释掉这一行即可得到月球引力在地球表面的分布。

hold on
axis equal
axis off
surf(x,y,z,'FaceColor','none','EdgeColor',[0.8 0.8 0.8]);
axis([-1.2 1.2 -1.2 1.2 -1.2 1.2])
quiver3(x,y,z,u,v,w);
view(-30,30);
hold off

1. ^ 月球产生的潮汐力应该大概是太阳的二倍多。但是，这不代表太阳对潮汐现象没有影响。

潮汐力

习题 1 谁是弄潮儿？

习题 1　谁是弄潮儿？