日晷的计算
贡献者: addis
- 一根垂直地面的杆如何判断时间?(只能用顶点判断)
1. 水平日晷
常见的水平日晷如图 1 和图 2 所示。把图片打印后,把直角三角形的底边垂直固定在半圆的 12 点方向,然后把半圆水平放于地面,12 点方向指向正北(地轴北)即可。此时三角形的斜边,也就是日晷的指针与地轴平行。太阳绕日晷指针以每小时 15°(一天 360°)的角速度匀速转动。
图 1:水平日晷(来自 Wikipedia)
该类型日晷的一个画图网页见这里。
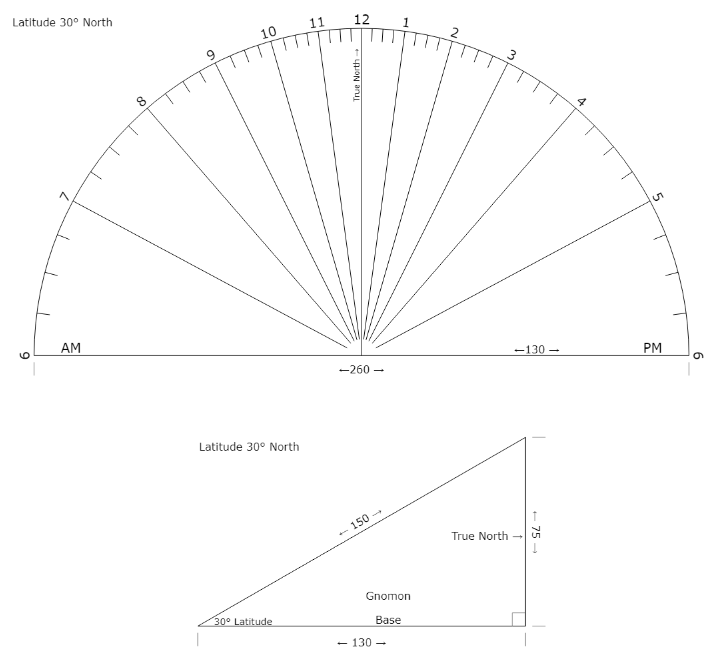
图 2:北纬 30° 的日晷
日晷圆盘上的刻度与所在纬度有关,若将其放在北极或南极,那么直角三角形的斜边就变为一个和地面垂直的线段,且表盘上的刻度是均匀的。相反,若把这种日晷放在赤道上,那么三角形的斜边将会与 12 点的刻度共线,此时这种日晷将失效。
刻度的具体计算并不复杂,公式为
\begin{equation}
\beta = \tan^{-1}(\sin\alpha \tan \theta)~.
\end{equation}
证明:令式 6 中 $\theta_2 = \pi/2$,$\theta_1 = \theta$ 即可。表盘的中心就是三棱锥顶点。
我们给出水平日晷的 Matlab 画图代码,结果类似图 2 。
代码 1:sunDial.m
alpha = pi/6; % 纬度
th = linspace(-pi/2, pi/2, 13);
beta = atan(sin(alpha).*tan(th));
th0 = linspace(-pi/2, pi/2, 1000);
figure; plot(cos(th0),sin(th0), 'k'); hold on;
for i = 1:13
plot([0,cos(beta(i))], [0,sin(beta(i))], 'k');
end
axis equal; view(-90, 90);
axis([-0.1, 1.1, -1.1, 1.1]);
2. 赤道平面日晷
另一种在任何纬度都适用的方案是让刻度盘始终与指针保持垂直,而指针始终平行于地轴。这种日晷的结构相对更复杂,但表盘上的刻度始终是均匀的,只需调整表盘与底座之间的夹角就能适用于不同纬度。
图 3:故宫的日晷(来自 Wikipedia)