贡献者: addis
预备知识 高中立体几何
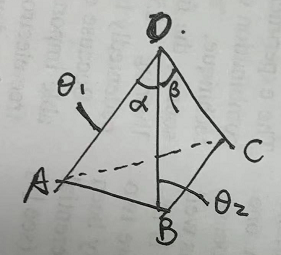
图 1:(左图)已知 $\theta_1$,$\theta_2$ 和 $\phi$ 求 $\alpha$;(右图)已知 $\theta$ 和 $\phi$ 求 $\gamma$
我们考虑如图 1 中三棱锥顶点 $O$ 处的 3 条棱和 3 个面之间的角度关系。这里涉及了三种角:两条棱之间的夹角(线线角)$\theta$,棱和面的夹角(线面角)$\gamma$,以及面和面的夹角(面面角)$\phi$。对给定的顶点,每种角都有各有 3 个,共 9 个。我们先不讨论底面 $ABC$ 的位置如何,如果顶点的三条棱的方向都确定,我们就说顶点的形状确定。
显然,我们无需知道所有 9 个角的大小才能确定顶点的形状。这里给出一个类似于三角形余弦定理的公式,将线线角和面面角联系起来。线线角可以类比余弦定理中的边长,面面角类比余弦定理中的夹角。
\begin{equation}
\cos\alpha = \cos\theta_1 \cos\theta_2 + \sin\theta_1 \sin\theta_2 \cos\phi~.
\end{equation}
如果已知该式中的 4 个角中的 3 个,就可以求出另一个角。与余弦定理类似,在求解 $\theta_1$ 或 $\theta_2$ 时可能存在两个解,也可能无解。注意如果我们交换 $\theta_1$ 和 $\theta_2$ 的值,上式仍然满足(这相当于创造一个镜像三棱锥)。
一个关于线面角的常用公式是
\begin{equation}
\sin\gamma = \sin\phi\sin\theta_1~,
\end{equation}
其中 $\gamma$ 是线段 $OB$ 和三角形 $OAC$ 的线面角。虽然乍看之下从该式无法判断出 $\gamma$ 是钝角还是锐角,但仔细分析可以发现若 $\phi$ 为钝角 $\gamma$ 也一定是钝角。
例 1 已知三个线线角求线面角
若已知 $\theta_1$,$\theta_2$ 和 $\alpha$,则
\begin{equation}
\cos\phi = \frac{\cos\alpha - \cos\theta_1 \cos\theta_2}{\sin\theta_1 \sin\theta_2}~.
\end{equation}
例 2
未完成:图
若一个正方形,一个正五边形,一个正六边形拼在一起,求正方形和正五边形的共同边与正六边形所成的线面角。
利用式 1 , 令正方形的内角为 $\theta_1 = \pi/2$,六边形的内角为 $\theta_2 = 2\pi/3$, 五边形的内角为 $\alpha = 3\pi/5$,代入式 1 解得正方形与六边形的二面角为 $\phi$ 为
\begin{equation}
\phi = \arccos\frac{\cos\alpha - \cos\theta_1 \cos\theta_2}{\sin\theta_1\sin\theta_2} \approx 1.936 \,\mathrm{rad} \approx 110.9^\circ~,
\end{equation}
再代入式 2 ,$\phi$ 是钝角,所以 $\gamma$ 也是钝角,所以
\begin{equation}
\gamma = \pi - \arcsin\left(\sin\phi \sin\theta_1\right) \approx 1.9357 \,\mathrm{rad} \approx 110.9^\circ~.
\end{equation}
这与 $\phi$ 相同,这是因为我们有一个正方形。
角边角
事实上解三棱锥顶角和解三角形类似,面面角可以看作三角形的 “角”,而两条棱之间的角可以看作三角形的 “边”。例如式 1 就可以看作 “边角边” 问题(已知 $\theta_1, \phi, \theta_2$)求第三边 $\alpha$。
那么我们再来看若已知 “角边角”($\theta_1, \alpha, \theta_2$)求下一边 $\beta$(图 2 )
图 2:角边角问题
$\beta$ 满足
\begin{equation}
(C_1^2 - S_\alpha^2 C_1^2 C_2^2 - C_\alpha^2 C_2^2)T_\beta^2 + 2S_\alpha C_\alpha S_1^2 C_2 T_\beta - S_1^2 S_\alpha^2 = 0~,
\end{equation}
其中 $C,S,T$ 分别代表 $\cos, \sin, \tan$,$C_1 = \cos\theta_1, C_2 = \cos\theta_2$。该式子可以直接使用两次 “边角边” 公式解出来。注意上式若存在两个解,必须剔除一个无意义的解。
1. 证明
我们可以用球坐标系来证明式 1 。令极坐标 $(\theta_1, \phi_1)$ 和 $(\theta_2, \phi_2)$ 代表的两个单位矢量的坐标分别为
\begin{equation}
(\sin\theta_1\cos\phi_1, \sin\theta_1\sin\phi_1, \cos\theta_1)~,
\qquad
(\sin\theta_2\cos\phi_2, \sin\theta_2\sin\phi_2, \cos\theta_2)~,
\end{equation}
\begin{equation}
\cos\alpha = \cos\theta_1 \cos\theta_2 + \sin\theta_1 \sin\theta_2 \cos\left(\phi_2 - \phi_1\right) ~.
\end{equation}
证毕。
再来证明式 2 ,我们仍然使用球坐标,将射线 OA 作为极轴,面 OAC 为 $xz$ 平面,线面角中 “线” 的极坐标为 $(1, \theta, \phi)$,该点的 $y$ 坐标为 $\sin\theta \sin\phi$ 而 $y = \sin\gamma$,所以 $\sin\gamma = \sin\theta \sin\phi$。证毕。