位移与应变

贡献者： ACertainUser

本文存在未完成的内容。

　　¹ 在应力中我们讨论了如何表示材料中各处的受力，现在我们讨论如何表示材料中各处的变形。此处我们只探讨小变形的情况，即材料变形的程度非常轻微。

1. 位移

图 1：材料变形后，材料中的每一点的位置发生改变

图 2：上图的叠加

　　材料变形后，材料中每一点都移动了。例如，原先位于 $ \boldsymbol{\mathbf{x}} _0$ 的点在变形后运动到了 $ \boldsymbol{\mathbf{a}} _0$ 位置，原先位于 $ \boldsymbol{\mathbf{x}} _1$ 的点运动到了 $ \boldsymbol{\mathbf{a}} _1$ 位置...如果我们在弹性力学中暂且假定 “变形前后，原先的一个点不会分裂为两个，也不会有两个点合并为一个”，那么我们就可以在点变形前的位置 $ \boldsymbol{\mathbf{x}} $ 与变形后的位置 $ \boldsymbol{\mathbf{a}} $ 之间建立一种映射$$ \boldsymbol{\mathbf{x}} \rightarrow \boldsymbol{\mathbf{a}} ~,$$亦即定义一个函数。$$ \boldsymbol{\mathbf{a}} = \boldsymbol{\mathbf{a}} ( \boldsymbol{\mathbf{x}} )~.$$

位移函数

　　为了更好地表示 $ \boldsymbol{\mathbf{x}} $ 处点位置的变化，我们定义位移函数

\begin{equation} \boldsymbol{\mathbf{u}} ( \boldsymbol{\mathbf{x}} ) = \boldsymbol{\mathbf{a}} ( \boldsymbol{\mathbf{x}} ) - \boldsymbol{\mathbf{x}} ~, \end{equation}

由此，点 $ \boldsymbol{\mathbf{x}} $ 的位置变化也可以表述为

\begin{equation} \boldsymbol{\mathbf{x}} + \boldsymbol{\mathbf{u}} ( \boldsymbol{\mathbf{x}} ) = \boldsymbol{\mathbf{a}} ( \boldsymbol{\mathbf{x}} ) ~. \end{equation}

　　 $ \boldsymbol{\mathbf{u}} $ 是一个矢量函数，也被称为位移场。它的 3 个分量都是关于点坐标的函数，分别表示点在 $x_1, x_2, x_3$²各方向上的位移。 $$ \boldsymbol{\mathbf{u}} ( \boldsymbol{\mathbf{x}} ) = \begin{pmatrix} u_1( \boldsymbol{\mathbf{x}} )\\ u_2( \boldsymbol{\mathbf{x}} )\\ u_3( \boldsymbol{\mathbf{x}} )\\ \end{pmatrix} = \begin{pmatrix} u_1(x_1, x_2, x_3)\\ u_2(x_1, x_2, x_3)\\ u_3(x_1, x_2, x_3)\\ \end{pmatrix}~. $$ 由于变形前后点不合并、分裂的性质，$ \boldsymbol{\mathbf{u}} ( \boldsymbol{\mathbf{x}} )$ 是一个 “好函数”，单值、连续且多阶可导。

2. 应变

　　有时我们使用应变$\varepsilon$ 来描述材料的变形。类似于应力，应变也定义在材料中的每一个微元处，可记为一个 $3\times3$ 的矩阵（二阶张量）.应变矩阵也是对称矩阵 $\varepsilon=\varepsilon^T$，有 $6$ 个独立变量。

\begin{equation} \varepsilon = \begin{pmatrix} \varepsilon_{11}&\varepsilon_{12}& \varepsilon_{13}\\ \varepsilon_{21}&\varepsilon_{22}& \varepsilon_{23}\\ \varepsilon_{31}&\varepsilon_{32}& \varepsilon_{33}\\ \end{pmatrix}~. \end{equation}

　　应变角标的含义与应力的类似，第一个角标表示面的法方向，第二个角标表示变形的方向。我们可将应变分为两类，正应变（两角标相同）与切应变（两角标不同）。

正应变

图 3：正应变示意图。改绘自冯西桥的《弹性力学》

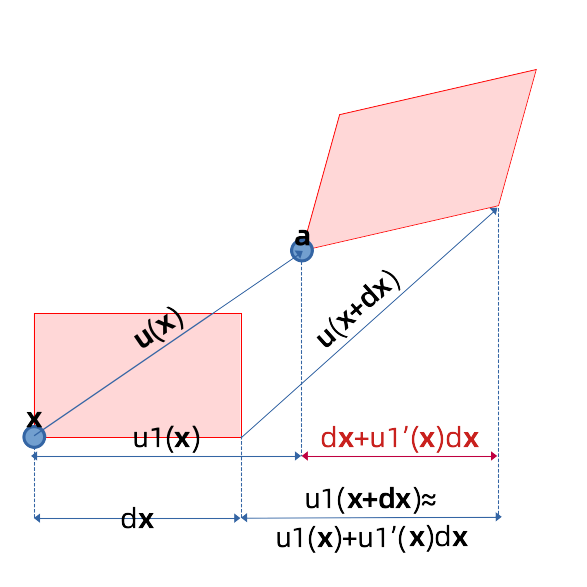
　　正应变与微元的长度变化有关。如图 3 所示，$x_1$ 方向上，微元的原本长度为 $l_0 = \,\mathrm{d}{x} _1$，变形后长度为 $ l = \,\mathrm{d}{x} _1+ \frac{\partial u_1}{\partial x_1} \,\mathrm{d}{x} _1$，长度变化 $\Delta l = l-l_0 = \frac{\partial u_1}{\partial x_1} \,\mathrm{d}{x} _1$，那么定义正应变

\begin{equation} \varepsilon_{11} = \frac{\Delta l}{l_0} = \frac{\partial u_1}{\partial x_1} ~. \end{equation}

切应变

图 4：切应变示意图。改绘自冯西桥的《弹性力学》

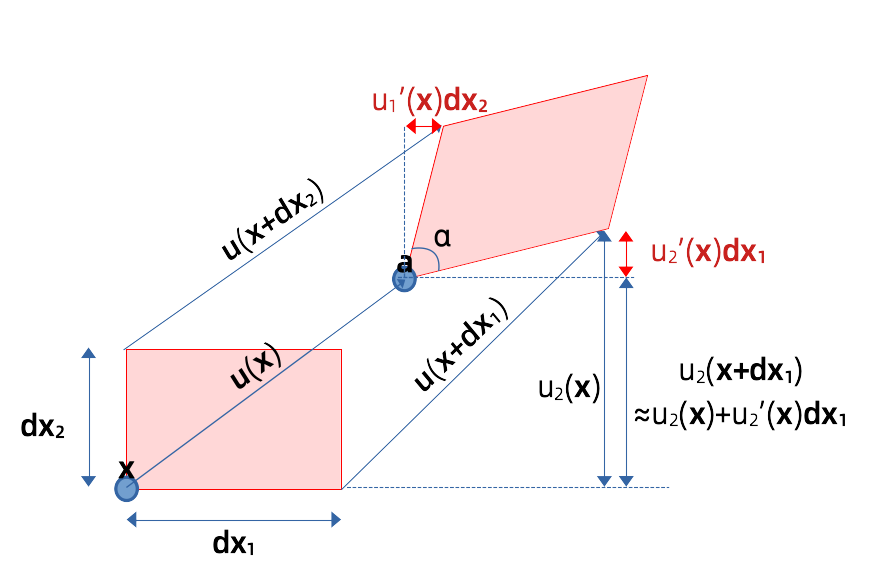
　　而切应变与微元的角度变化有关。如图 4 所示，定义切应变

\begin{equation} \varepsilon_{12} = \frac{1}{2}(90^\circ - \alpha) = \frac{1}{2}\left( \frac{\partial u_1}{\partial x_2} + \frac{\partial u_2}{\partial x_1} \right)~, \end{equation}

有时也使用工程切应变 $\gamma$。别紧张，他们只是相差一个系数

\begin{equation} \gamma_{12} = 2\varepsilon_{12} = 90^\circ - \alpha~. \end{equation}

3. 应变几何方程

　　推广上一节的结论，我们共可以得到 $6$ 个联系应变与位移的独立方程。这 $6$ 个方程被称为应变几何方程。

\begin{equation} \varepsilon_{ij} = \frac{1}{2}\left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right) \qquad (i,j=1,2,3)~. \end{equation}

4. 应变协调方程

5. 画廊：经典的应变类型

　　图中黑色为原微元体，红色为变形后的微元体。

图 5：$u_1=1.5$。各应变均为 $0$，微元形状不变、只发生平移。

图 6：$u_1=0.2x_1$。$\varepsilon_{11}=0.2$（其余项为 $0$），微元发生拉伸变形

图 7：$u_1=0.2x_2$. $\varepsilon_{12}=0.1$,微元发生简单的剪切变形

图 8：$u_1=0.2x_2, u_2=0.2x_1$.$\varepsilon_{12}=0.2$，微元发生剪切变形

图 9：同上，但是是俯视图

6. 附录：应变模拟器

　　用以绘制上述应变示意图的 Matlab 代码

%定义位移函数，你可以设置自己的线性位移函数
u1 = @(x,y,z) -0.2*x + 0.2*y;
u2 = @(x,y,z) 0;
u3 = @(x,y,z) 0;

A(1,:)=[0,0,0];
A(2,:)=[1,0,0];
A(3,:)=[1,1,0];
A(4,:)=[0,1,0];
A(5,:)=[0,1,1];
A(6,:)=[0,0,1];
A(7,:)=[1,0,1];
A(8,:)=[1,1,1];

hold on
axis equal

%绘制顶点
%for i = 1:8
%    scatter3(A(i,1),A(i,2),A(i,3),'k');
%endfor

view(-30,60)
xlabel('Axis 1','fontsize',15)
ylabel('Axis 2','fontsize',15)
zlabel('Axis 3','fontsize',15)

line([A(1,1), A(2,1)],[A(1,2), A(2,2)],[A(1,3), A(2,3)],'color','k');
line([A(1,1), A(4,1)],[A(1,2), A(4,2)],[A(1,3), A(4,3)],'color','k');
line([A(1,1), A(6,1)],[A(1,2), A(6,2)],[A(1,3), A(6,3)],'color','k');

line([A(2,1), A(7,1)],[A(2,2), A(7,2)],[A(2,3), A(7,3)],'color','k');
line([A(2,1), A(3,1)],[A(2,2), A(3,2)],[A(2,3), A(3,3)],'color','k');

line([A(3,1), A(4,1)],[A(3,2), A(4,2)],[A(3,3), A(4,3)],'color','k');
line([A(3,1), A(8,1)],[A(3,2), A(8,2)],[A(3,3), A(8,3)],'color','k');

line([A(4,1), A(5,1)],[A(4,2), A(5,2)],[A(4,3), A(5,3)],'color','k');

line([A(6,1), A(5,1)],[A(6,2), A(5,2)],[A(6,3), A(5,3)],'color','k');
line([A(6,1), A(7,1)],[A(6,2), A(7,2)],[A(6,3), A(7,3)],'color','k');

line([A(8,1), A(5,1)],[A(8,2), A(5,2)],[A(8,3), A(5,3)],'color','k');
line([A(8,1), A(7,1)],[A(8,2), A(7,2)],[A(8,3), A(7,3)],'color','k');

for i = 1:8
    B(i,1) = u1(A(i,1),A(i,2),A(i,3))+A(i,1);
    B(i,2) = u2(A(i,1),A(i,2),A(i,3))+A(i,2);
    B(i,3) = u3(A(i,1),A(i,2),A(i,3))+A(i,3);
endfor

%for i = 1:8
%    scatter3(B(i,1),B(i,2),B(i,3),'r');
%endfor

line([B(1,1), B(2,1)],[B(1,2), B(2,2)],[B(1,3), B(2,3)],'color','r');
line([B(1,1), B(4,1)],[B(1,2), B(4,2)],[B(1,3), B(4,3)],'color','r');
line([B(1,1), B(6,1)],[B(1,2), B(6,2)],[B(1,3), B(6,3)],'color','r');

line([B(2,1), B(7,1)],[B(2,2), B(7,2)],[B(2,3), B(7,3)],'color','r');
line([B(2,1), B(3,1)],[B(2,2), B(3,2)],[B(2,3), B(3,3)],'color','r');

line([B(3,1), B(4,1)],[B(3,2), B(4,2)],[B(3,3), B(4,3)],'color','r');
line([B(3,1), B(8,1)],[B(3,2), B(8,2)],[B(3,3), B(8,3)],'color','r');

line([B(4,1), B(5,1)],[B(4,2), B(5,2)],[B(4,3), B(5,3)],'color','r');

line([B(6,1), B(5,1)],[B(6,2), B(5,2)],[B(6,3), B(5,3)],'color','r');
line([B(6,1), B(7,1)],[B(6,2), B(7,2)],[B(6,3), B(7,3)],'color','r');

line([B(8,1), B(5,1)],[B(8,2), B(5,2)],[B(8,3), B(5,3)],'color','r');
line([B(8,1), B(7,1)],[B(8,2), B(7,2)],[B(8,3), B(7,3)],'color','r');

图 10：简单的剪切变形

　　另一个以点阵代替正方体的实现的 Matlab 代码：

clc
clear

function s = SHPERE(x,y,z,r)
  [X,Y,Z] = sphere(50);
  X = r*X+x;
  Y = r*Y+y;
  Z = r*Z+z;
  s = surf(X,Y,Z);
end

u1 = @(x,y,z) 0.2*y;
u2 = @(x,y,z) -0.05*y;
u3 = @(x,y,z) 0;

hold on
axis equal

for x = 0:3
  for y = 0:3
    for z = 0:3
      a = u1(x,y,z)+x;
      b = u2(x,y,z)+y;
      c = u3(x,y,z)+z;
      SPHERE(a,b,c,0.5);
    end
  end
end

1. ^ 本文参考了冯西桥的《弹性力学》课程与陆明万的《弹性理论基础》
2. ^ 为了方便表示，以 $x_1, x_2, x_3$ 轴代指 $x,y,z$ 轴