SciPy 数值微分与积分

                     

贡献者： shizy0808; addis; Li Hao-Hao

预备知识　Python 入门

　　 SciPy 函数库在 NumPy 库的基础上增加了众多的数学、科学以及工程计算中常用的库函数。例如线性代数、常微分方程数值求解、信号处理、图像处理、稀疏矩阵等等。 使用 SciPy 库之前需要先导入库， 

import  scipy#导入scipy中所有模块
from scipy import integrate#导入其中积分模块

1. 数值积分

　　 数值积分是对定积分的数值求解。例如可以利用数值积分计算某个形状的面积。下面让我们来考虑一下如何计算半径为 1 的半圆的面积，根据圆的面积公式，其面积应该等于 $\pi$。单位半圆曲线可以用函数 half_circle() 表示，对应计算积分的代码如下： 

def half_circle(x):
    return (1-x**2)**0.5

from scipy import integrate
res, err = integrate.quad(half_circle, -1, 1)
print(res,err)
输出：
1.5707963267948983 1.0002354500215915e-09
此处调用了积分模块下的 quad 函数，这里不仅返回了积分结果，还给出来计算误差。多重定积分的求值可以通过多次调用 quad 函数实现，为了调用方便，integrate 库提供了 dblquad 函数 进行二重定积分，tplquad 函数进行三重定积分。

　　 dblquad 函数的调用方式为： 

dblquad(func2d, a, b, gfun, hfun, args=())
对于 func2d(y,x) 函数进行二重积分，其中 a,b 为变量 $x$ 的积分区间，$ a < b $，而 gfun(x) 到 hfun(x) 为变量 $y$ 的积分区间，注意被积函数中变量 $ y $ 与 $ x $ 的位置必须和相应的积分限位置对应。args=() 为向函数 func2d(y,x) 中传递的参量，比如函数 func2d(y,x,c,d,f)，其中 c,d,f 为向被积函数传递的参量，而 y,x 为积分变量，这一项是可选择的，若没有需要传递的参量可以不加该项。

　　 tblquad 函数的调用方式与上面一样。

2. 数值解微分方程组

　　 scipy.integrate 库提供了数值积分和常微分方程组求解算法 odeint。 odeint() 函数需要至少三个变量，第一个是微分方程函数，第二个是微分方程初值，第三个是微分的自变量。

　　 下面让我们来看看如何用 odeint 计算十分经典的洛仑兹吸引子的轨迹。洛仑兹吸引子由下面的三个微分方程定义：

\begin{align} &\dot{x}=\sigma~.\\ &\dot{y}=x(\rho-y)~.\\ &\dot{z}=xy-\beta~. \end{align} 
from scipy.integrate import odeint
import numpy as np
def lorenz(w, t, p, r, b):
    # 给出位置矢量w，和三个参数p, r, b计算出
    # dx/dt, dy/dt, dz/dt的值
    x, y, z = w
    # 直接与lorenz的计算公式对应
    return np.array([p*(y-x), x*(r-z)-y, x*y-b*z])

t = np.arange(0, 30, 0.01) # 创建时间点
# 调用ode对lorenz进行求解， 用两个不同的初始值
track1 = odeint(lorenz, (0.0, 1.00, 0.0), t, args=(10.0, 28.0, 3.0))
track2 = odeint(lorenz, (0.0, 1.01, 0.0), t, args=(10.0, 28.0, 3.0))
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
fig = plt.figure()
ax = Axes3D(fig)
ax.plot(track1[:,0], track1[:,1], track1[:,2])
ax.plot(track2[:,0], track2[:,1], track2[:,2])
plt.show()
结果如图 1 所示。

图
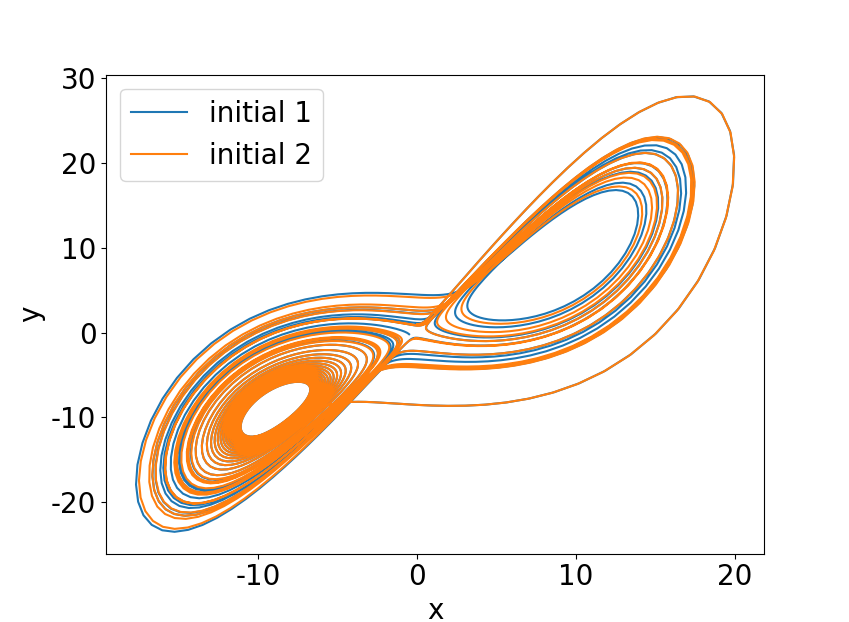
图 1：洛伦兹微分方程数值解

　　 这里我们还使用到了第四个参数 args，它是一个 tuple 类型，给函数传递额外的参数。我们看到即使初始值只相差 0.01，两条运动轨迹也是完全不同的。 在程序中先定义一个 lorenz 函数，它的任务是计算出某个位置的各个方向的微分值，这个计算直接根据洛仑兹吸引子的公式得出。然后调用 odeint，对微分方程求解，odeint 有许多参数，这里用到的四个参数分别为：

                     

© 小时科技 保留一切权利