SciPy 最小二乘法

贡献者： addis; shizy0808

预备知识　Python 入门

1. 最小二乘拟合

　　最小二乘法是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。

　　通常情况下最小二乘法是这样的：给定一组数，假设是二维数据。 $(x_{1}, y_{1}), (x_{2}, y_{2}), \dots, (x_{n}, y_{n})$ ,并且 $x, y$ 是相关的。假设满足方程

\begin{matrix} (1) & y = f (x), \end{matrix}

但是这个方程我们是不知道具体什么样的。我们找到一个近似函数

\begin{matrix} (2) & y = g (x) . \end{matrix}

　　对于每一个点 $(x_{i}, y_{i})$ 有 $y_{i} = g (x_{i}) + ϵ_{i}$ ， $ϵ_{i}$ 是残差。那么总的残差平方和为

\begin{matrix} (3) & e r r = \sum_{i = 1}^{n} [y_{i} - g (x_{i})]^{2}, \end{matrix}

那么我们就是要找到这样的

g (x)

使得如下公式中的

e r r

函数最小。这种算法被称之为最小二乘拟合（Least-square fitting）。

　　 scipy 中的子函数库 optimize 已经提供了实现最小二乘拟合算法的函数 leastsq。下面是用 leastsq 进行数据拟合的一个例子： $y = A \sin (2 π x + θ)$ 。

import numpy as np
from scipy.optimize import leastsq
import pylab as plt
import matplotlib as mpl

mpl.rcParams["font.sans-serif"]=['kaiti']
mpl.rcParams['axes.unicode_minus']=False
def func(x, p):
"""
数据拟合所用的函数: A*sin(2*pi*k*x + theta)
"""
 A, k, theta = p
 return A*np.sin(2*np.pi*k*x+theta)

def residuals(p, y, x):
"""
实验数据x, y和拟合函数之间的差，p为拟合需要找到的系数
"""
  return y - func(x, p)

x = np.linspace(0, -2*np.pi, 100)
A, k, theta = 10, 0.34, np.pi/6 # 真实数据的函数参数
y0 = func(x, [A, k, theta]) # 真实数据
y1 = y0 + 2 * np.random.randn(len(x)) # 加入噪声之后的实验数据
p0 = [7, 0.2, 0] # 第一次猜测的函数拟合参数

# 调用leastsq进行数据拟合
# residuals为计算误差的函数
# p0为拟合参数的初始值
# args为需要拟合的实验数据
plsq = leastsq(residuals, p0, args=(y1, x))

print(u"真实参数:", [A, k, theta])
print(u"拟合参数", plsq[0]) # 实验数据拟合后的参数

plt.plot(x, y0, label=u"真实数据")
plt.plot(x, y1, label=u"\autoref{fig_PyFit_1}带噪声的实验数据")
plt.plot(x, func(x, plsq[0]), label=u"拟合数据")
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
plt.legend()
plt.show()

结果图像如图 1 所示。

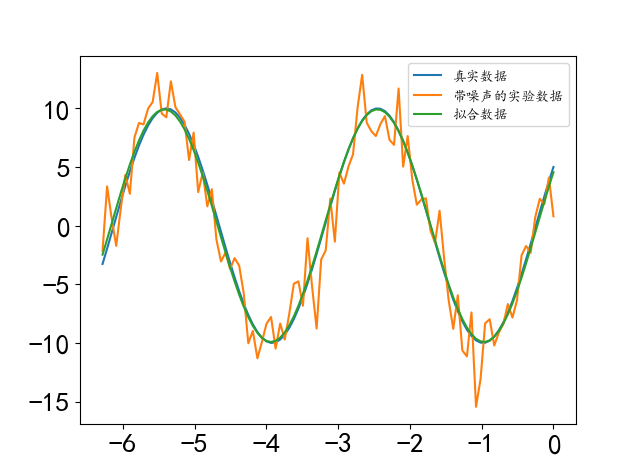
图 1：最小二乘法 1

　　我们看到拟合参数虽然和真实参数完全不同，但是由于正弦函数具有周期性，实际上拟合参数得到的函数和真实参数对应的函数是一致的。

　　第二个例子：拟合 $y = k x + b$ 。

# -*- coding: utf-8 -*-
import numpy as np
from scipy.optimize import leastsq
import pylab as plt
import matplotlib as mpl

mpl.rcParams["font.sans-serif"]=['kaiti']
mpl.rcParams['axes.unicode_minus']=False
def func(x, p):
 k,b = p
 return k*x+b

def residuals(p, y, x):
  """
 实验数据x, y和拟合函数之间的差，p为拟合需要找到的系数
 """
  return y - func(x, p)

x = np.linspace(0, -2*np.pi, 100)
k,b = 10, 5.0 # 真实数据的函数参数
y0 = func(x, [k,b]) # 真实数据
y1 = y0 + 2 * np.random.randn(len(x)) # 加入噪声之后的实验数据
p0 = [7, 0.2] # 第一次猜测的函数拟合参数

 # 调用leastsq进行数据拟合
 # residuals为计算误差的函数
 # p0为拟合参数的初始值
 # args为需要拟合的实验数据
plsq = leastsq(residuals, p0, args=(y1, x))

print(u"真实参数:", [k,b])
print(u"拟合参数", plsq[0]) # 实验数据拟合后的参数

plt.plot(x, y0, label=u"真实数据")
plt.plot(x, y1, label=u"带噪声的实验数据")
plt.plot(x, func(x, plsq[0]), label=u"拟合数据")
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
plt.legend()
plt.show()

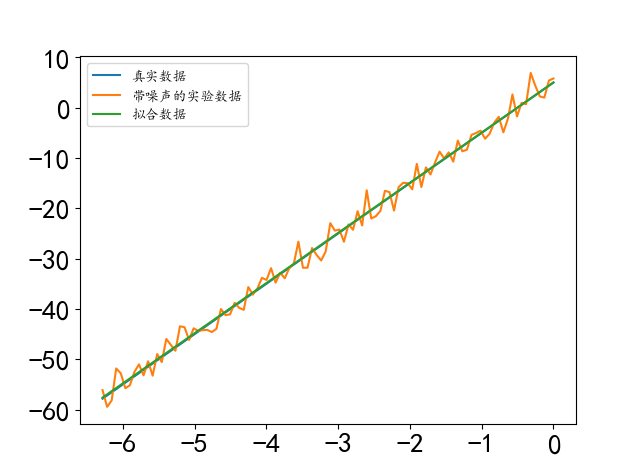
拟合结果：真实参数为 [10, 5.0]，拟合参数 [9.96688563 5.0180872]。图像如图 2 所示。

图 2：最小二乘法 2