给高中生的量子力学简介
贡献者: addis
1. 简介
对象:对量子物理比较感兴趣的高中生。数学要求不高,物理图像为主。
背景知识
- 双缝干涉
- 德布罗意物质波
- 玻尔原子模型
- 电子的双缝干涉
一维波动力学(量子)
- 概率波和波包
- 自由高斯波包
- 势垒散射、隧道效应
- 无限深势阱
说明:
- 量子力学和波有什么关系?
- 一维是什么?
2. 双缝干涉
平面波
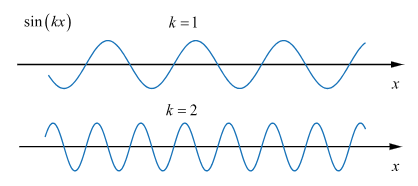
一维平面波:振幅,波长 $\lambda$,波速 $v$,相位,初相位 $\phi$
图 1:一维平面波 $\sin[k(x-vt) + \phi]$,由负无穷延伸至正无穷。
\begin{equation}
y = A \sin[k(x-vt) + \phi] = A \sin\left(kx - \omega t + \phi\right) ~,
\end{equation}
\begin{equation}
\omega = kv~,
\end{equation}
\begin{equation}
\lambda = \frac{2\pi}{k}~,
\qquad
T = \frac{2\pi}{\omega}~.
\end{equation}
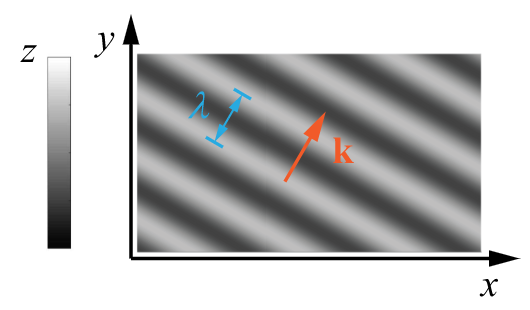
二维和三维平面波
图 2:二维平面波
\begin{equation}
s = A \cos\left( \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} - \omega t + \varphi_0\right) ~.
\end{equation}
波的叠加与干涉
波的叠加就是做加法,相位差决定干涉结果
一维的波的叠加
什么是相干性?
二维:
图 3:水波的干涉
图 4:光的双缝干涉
双缝干涉 PhET 演示。
为什么用手电筒做不出?不相干
3. 德布罗意物质波
对于光子
\begin{equation}
\begin{aligned}
p &= mc~,
\\
E &= mc^2 = pc = h\nu = \frac{hc}{\lambda}~.
\end{aligned}
\end{equation}
德布罗意假设(两条不含 $c$ 的)
\begin{equation}
\lambda = \frac{h}{p}~,
\end{equation}
\begin{equation}
E = h\nu~.
\end{equation}
左边描述粒子性,右边描述波动性
4. 概率波和波包
5. 电子的双缝干涉
图 5:即使每次放出一个电子,仍然会有干涉条纹
6. 玻尔原子模型
图 6:类氢原子
\begin{equation}
\begin{aligned}
F &= \frac{1}{4\pi \epsilon_0} \frac{(Ze)e}{r^2}~,
\\
F &= ma = m\frac{v^2}{r}~.
\end{aligned}
\end{equation}
角动量量子化条件
\begin{equation}
L = mvr = n\hbar~,
\end{equation}
\begin{equation}
2\pi r = n \lambda = n \frac{h}{mv}~.
\end{equation}
能级公式
\begin{equation}
E_n = - \frac{m k e^4}{2 \hbar ^2} \frac{Z^2}{n^2} \approx - 13.6 \,\mathrm{eV} \frac{Z^2}{n^2}
\qquad (n = 1, 2, \dots)~.
\end{equation}