贡献者: zhousiyi
预备知识 量子力学
QED 可能是我们有的最好的基本理论了。这个理论由一系列简单的方程(麦克斯韦方程和狄拉克方程)组成。方程的形式可以由相对论不变性定出来。这些方程的解决定着宏观和微观的物理。
费曼图给了这个理论同样优雅的计算步骤。假如我们想计算某个过程的发生概率,我们可以遵照如下步骤:
- 画出这个过程对应的费曼图
- 根据图写出散射振幅的表达式
- 化简表达式
1. 最简单的情形
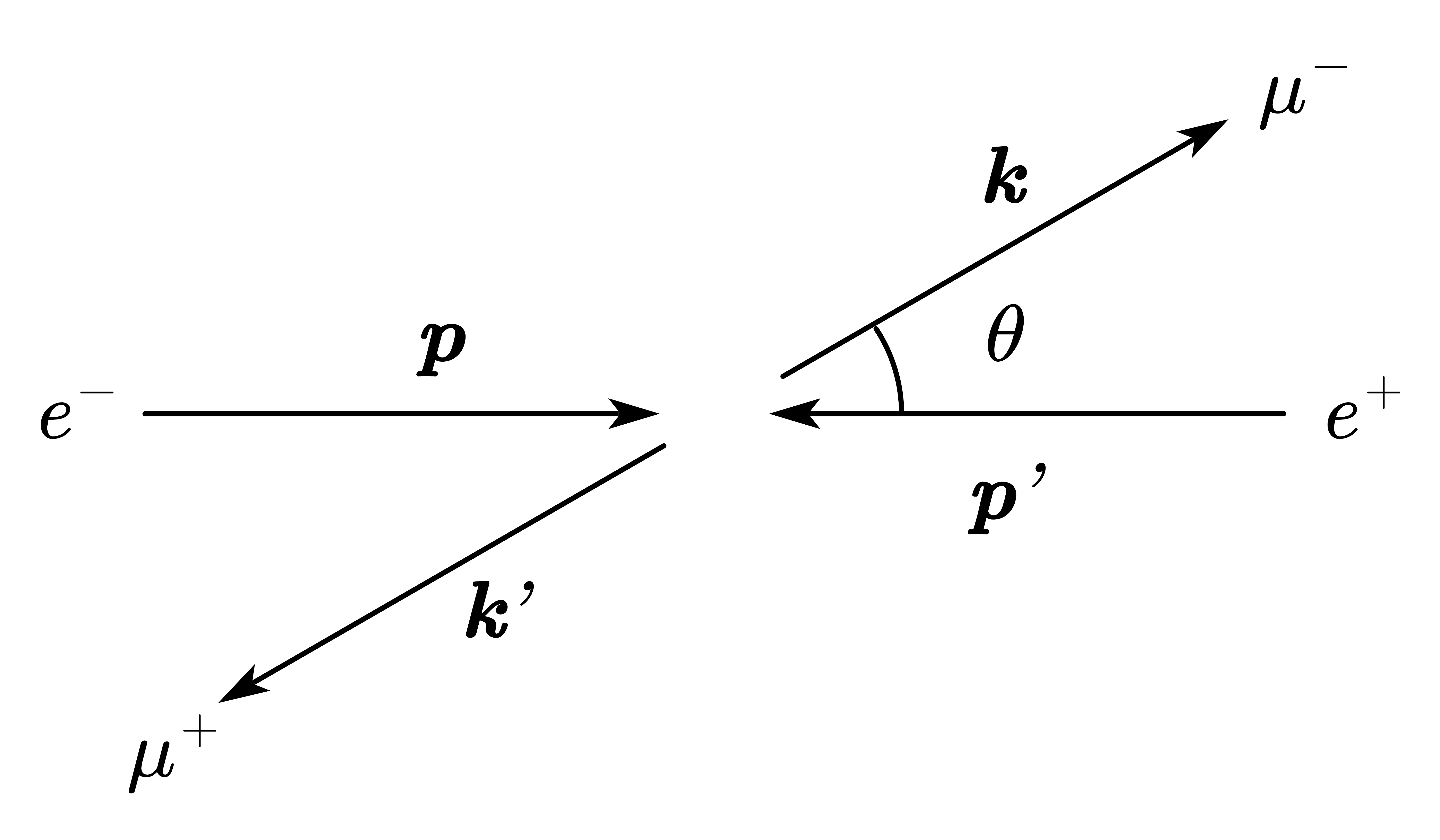
大多数粒子物理实验跟散射有关。所以,量子场论中最常见的就是散射振幅的计算了。那么我们现在就来做一个 QED 里面最简单的计算,也就是正负电子湮灭产生一对新的正负轻子(比如说 $\mu$ 子)的过程。相关过程的示意图如下:
图 1:$e^+e^-\rightarrow\mu^+\mu^-$ 过程的费曼图
实验上,如果我们把一束电子束射到一束正电子束上,就能够实现这个过程。可观测量是这个过程的散射截面。散射截面是这个过程的值信息能力以及入射电子与出射 $\mu$ 子之间的夹角。
为了简单起见,我们使用质心系。则这四个动量之间有如下关系:
\begin{equation}
\mathbf p' = - \mathbf p~, \quad \mathbf k'=-\mathbf k~.
\end{equation}
另外,我们需要假设质心系能量远大于电子以及 $\mu$ 子的质量。于是我们有
\begin{equation}
|\mathbf p| = |\mathbf p'| = |\mathbf k| = |\mathbf k'| = E = E_{\rm cm}/2~.
\end{equation}
我们约定粗体代表三动量,斜体代表四动量。
因为电子和 $\mu$ 子的自旋均为 $1/2$,我们必须指定自旋的方向。那么比较方便的做法是取这个例子运动的方向作为坐标轴。那么每个粒子就会有平行于或者反平行于这个坐标轴的自旋。
但是实际上来说,电子和正电子束一般都是没有极化的。$\mu$ 子探测器也通常探测不到 $\mu$ 子的自旋。所以一般的做法是对电子和正电子的自旋求平均,而对 $\mu$ 子的自旋求和。
微分散射截面是一个很重要的物理量。它的定义如下
定义 1 微分散射截面
\begin{equation}
\frac{d\sigma}{d\Omega} = \frac{1}{64\pi^2E_{\rm cm}^2}\cdot |\mathcal M|^2~.
\end{equation}
$E_{\rm cm}^{-2}$ 给出了微分散射截面的正确的量纲。散射振幅 $\mathcal M$ 是无量纲的。$16\pi^2$ 只是约定。散射振幅的物理意义是一个过程发生的量子力学概率振幅。那么知道如何计算散射振幅是一个非常重要的技术。这个式子只是用于质心系并且末态是两个无质量例子的情况。更为一般的式子我们将在后面讲到。
需要注意的是,即使是对于如此简单的过程,$\mathcal M$ 的精确表达式也是未知的。但幸运的是,我们可以通过微扰展开的方法来对 $\mathcal M$ 进行近似计算。这个计算方法是费曼发明的。他发明了一套 “费曼图” 技术,让 $\mathcal M$ 的计算变得简单而且易于操作。
费曼图形象地画出了基本粒子的运动。
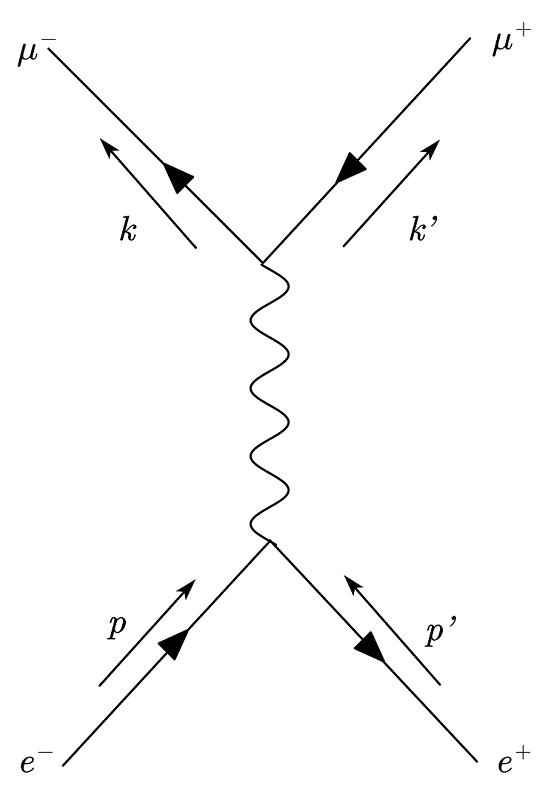
图 2:$e^+e^-\rightarrow\mu^+\mu^-$ 过程的费曼图
这个图时间是自下而上流动的。左右代表空间。所以这个图的意思是正负电子湮灭,产生了光子,最后生成了一对正负 $\mu$ 子。图中的波浪线就代表光子。光子的四动量 $q$ 可以用动量守恒算出来
\begin{equation}
q=p+p'=q+q'~,
\end{equation}
我们可以根据费曼规则直接写下 $\mathcal M$。那么因为我们现在还没有学这个规则,我们来简略说一下它的思路。首先,在量子力学的微扰理论中,我们可以用如下公式计算振幅
\begin{equation}
\langle \text{末态} |H_I| \text{初态} \rangle~.
\end{equation}
这里 $H_I$ 代表相互作用哈密顿量。那么在我们这个例子里,因为初态是两个电子,所以
\begin{equation}
| \text{初态} \rangle = | e^+ e^- \rangle~,
\end{equation}
同样的,末态是
\begin{equation}
\langle \text{末态} | = \langle \mu^+ \mu^- |~,
\end{equation}
电子和 $\mu$ 子的相互作用只能通过交换光子来实现。所以
式 5 没有一阶贡献。最低阶贡献是二阶的。贡献如下
\begin{equation}
\mathcal M = \langle \mu^+ \mu^- | H_I | \gamma \rangle^\mu \langle \gamma | H_I | e^+ e^- \rangle_\mu ~,
\end{equation}
这是一个比较粗糙的说法。电子的外腿相当于因子 $| e^+ e^- \rangle $,$\mu$ 子外腿相当于因子 $\langle \mu^+ \mu^- |$.顶点相当于是 $H_I$。光子内线相当于因子 $|\gamma\rangle\langle\gamma|$。这里 $\mu$ 的意思是光子是个矢量粒子。那么实际上散射振幅 $\mathcal M$ 可以按照
式 8 拆解为两个四矢量的点积。$\mathcal M$ 本身是一个洛仑兹不变的标量。
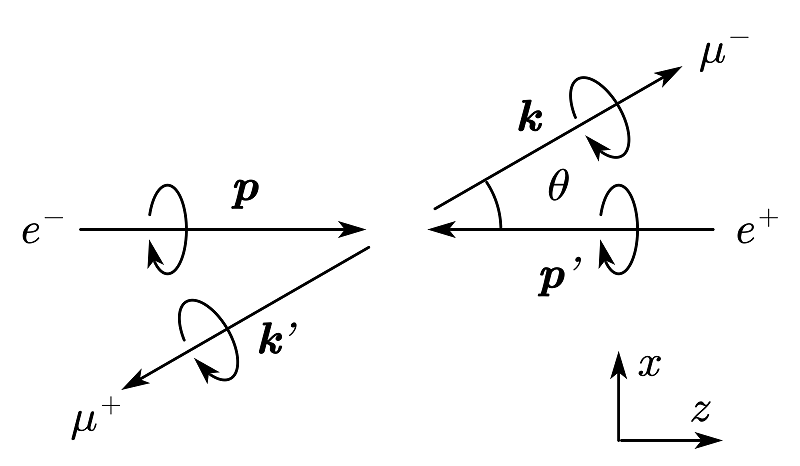
因为电子和光子的耦合强度是 $e$,$\langle \gamma | H_I | e^+ e^- \rangle_\mu$ 应正比于 $e$. 我们接下来考虑一种可能的自旋方向,如图 3 所示
图 3:$e^+e^-\rightarrow\mu^+\mu^-$ 过程的极化示意图
电子和 $\mu$ 子的自旋都和他们的运动方向平行,也就是说它们是右手的。反电子和反 $\mu$ 子都是左手的。电子和正电子的自旋加起来相当于是 $z$ 轴方向一个单位的角动量。因为 $H_I$ 是保持角动量守恒的,光子必须有正确的极化矢量,才能保证角动量守恒。我们设光子的极化矢量为 $\epsilon^\mu =(0,1,i,0)$,则
\begin{equation}
\langle \gamma | H_I | e^+ e^- \rangle^\mu \propto e (0,1,i ,0)~,
\end{equation}
$\mu$ 子的矩阵元应该具有跟 $\mu$ 子的运动方向相对应的极化矢量。也就是说我们应该把
式 3 在 $xz$ 平面旋转 $\theta$ 角
\begin{equation}
\langle \gamma| H_I \mu^+\mu^-\rangle^\mu \propto e (0,\cos\theta, i, - \sin\theta) ~.
\end{equation}
那么计算散射振幅的话只需要把
式 3 点乘
式 3 就可以了,结果如下
\begin{equation}
\mathcal M(RL\rightarrow RL) = - e^2 (1+\cos\theta)~.
\end{equation}
当然这里只是一个粗糙的估计,并不能确定总体的系数。但因为我们预先知道了答案,采取了
式 3 这样的约定,我们这个结果的总体的系数是正确的。当 $\theta = \pi$ 的时候,散射振幅为零。这是因为一个角动量是沿着 $+z$ 方向的态,和一个角动量是沿着 $-z$ 方向的态之间,是没有散射振幅的。
现在我们来考虑电子和正电子都是右手的情况。因为它们的总的自旋角动量是零,但光子必须有角动量。所以 $\mathcal M (RR \rightarrow RL)$ 的振幅为零。另外几个非零的振幅列举如下
\begin{equation}
\mathcal M(RL\rightarrow LR) = - e^2(1-\cos\theta) ~,
\end{equation}
\begin{equation}
\mathcal M(LR\rightarrow RL) = - e^2 (1-\cos\theta)~,
\end{equation}
\begin{equation}
\mathcal M(LR \rightarrow LR) = - e^2(1+\cos\theta)~,
\end{equation}
把这些结果代入
式 3 可得
\begin{equation}
\frac{d\sigma}{d\Omega} = \frac{\alpha^2}{4E_{\rm cm}^2}(1+\cos^2\theta) ~.
\end{equation}
其中 $\alpha = e^2/4\pi=1/137$. 我们把上面的微分截面对 $\theta$ 和 $\phi$ 进行积分可以得到总散射截面,结果如下
\begin{equation}
\sigma_{\rm total} = \frac{4\pi \alpha^2}{3E_{\rm cm}^2}~,
\end{equation}
和
式 16 跟实验的结果相比相差 10%。这是因为我们只考虑了最低阶的树图的贡献的原因。我们将在后面学习如何进行更精确的计算。