纯滚动
贡献者: なりもと; addis
1. 纯滚动
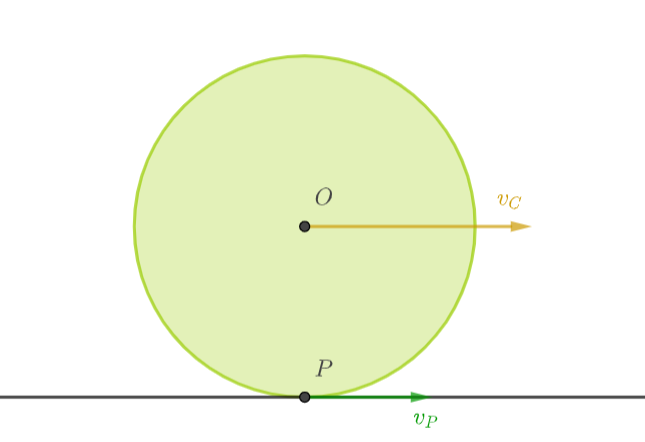
接触面之间没有相对滑动的滚动称为纯滚动,或称无滑动滚动。 对于纯滚动的刚体,与接触面相接触的点保持静止。以质量分布均匀的球在水平面上运动为例,如图 1
图 1:纯滚动
应该满足 $v_P= \boldsymbol{\mathbf{0}} $,并且 P 点处的切向加速度为 0。
2. 纯滚动的运动学判据
对于纯滚动的物体,有一定的约束条件。(这里讨论的是如球、圆柱之类的圆形刚体)
\begin{equation}
\begin{aligned}
v_C&=R\omega~,\\
a_C&=R\beta~.
\end{aligned}
\end{equation}
3. 纯滚动中摩擦力不做功
假设图 1 中的刚体向前位移了 $\mathrm{d} \boldsymbol{\mathbf{x}} $,角位移为 $\mathrm{d} \boldsymbol{\mathbf{\theta}} $,刚体所受的摩擦力为 $ \boldsymbol{\mathbf{f}} $,那么摩擦力做的功可以分为两部分:一部分是 $ \boldsymbol{\mathbf{f}} $ 沿 $\mathrm{d} \boldsymbol{\mathbf{x}} $ 做的功,另一部分是 $ \boldsymbol{\mathbf{f}} $ 的力矩沿 $ \boldsymbol{\mathbf{\theta}} $ 做的功
\begin{equation}
\begin{aligned}
W&= \boldsymbol{\mathbf{f}} \cdot\mathrm{d} \boldsymbol{\mathbf{x}} +( \boldsymbol{\mathbf{R}} \times \boldsymbol{\mathbf{f}} )\cdot\mathrm{d} \boldsymbol{\mathbf{\theta}} \\
&=-f\mathrm{d} x+fR\mathrm{d} \theta~,
\end{aligned}
\end{equation}
于是
\begin{equation}
W=f(-\mathrm{d} x+R\mathrm{d} \theta)=0~.
\end{equation}