偏导数（简明微积分）

贡献者： addis; 钱昭霖; ACertainUser; EienMiku

预备知识　导数

　　对一个多元函数 $y = f(x_1, x_2 \dots x_i \dots)$，如果求导时只把 $x_i$ 看成自变量，剩下的 $x_{j \ne i}$ 都看做常数，得到的导数就叫函数（关于 $x_i$）的偏导数。以二元函数 $z=f(x,y)$ 为例，对 $x$ 的偏导数常可记为以下几种表达式的其中之一：

\begin{equation} \frac{\partial z}{\partial x} ~, \qquad \frac{\partial f}{\partial x} ~, \qquad f_x~, \qquad \left( \frac{\partial f}{\partial x} \right) _y~. \end{equation}

最后一种记号在括号右下角声明函数中所有保持不变的自变量，这在一些情况下能避免混淆（见子节 2 ）。

例 1　

　　对于函数 $f(x,y) = x^2 + 2 y^2 + 2xy$，两个偏导数分别为

\begin{equation} \frac{\partial f}{\partial x} = 2x + 2y~, \qquad \frac{\partial f}{\partial y} = 4y + 2x~. \end{equation}

例 2　

　　对于函数 $z = \sin\left(y\cos x\right) + \cos ^2 x$

\begin{equation} \begin{aligned} \frac{\partial z}{\partial x} &= - y \cos\left(y\cos x\right) \sin x - 2\cos x\sin x = - y \cos\left(y\cos x\right) \sin x - \sin 2x~,\\ \frac{\partial z}{\partial y} &= \cos\left(y\cos x\right) \cos x~. \end{aligned} \end{equation}

1. 几何意义

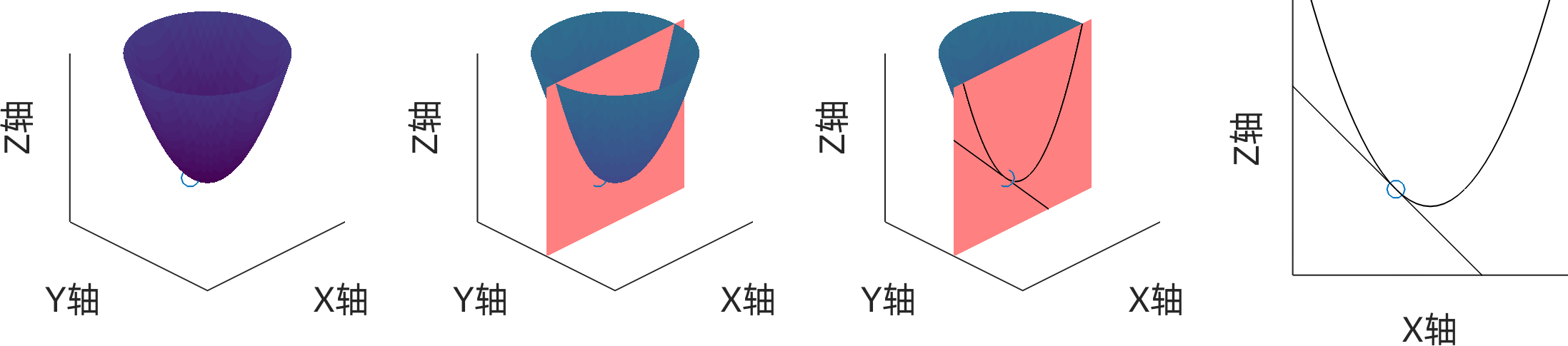
图 1：偏导数

　　类比导数的几何意义（曲线的斜率），若在三维直角坐标系中画出曲面 $f(x,y)$，则 $ \partial f/\partial x $ 和 $ \partial f/\partial y $ 分别是是某点处曲面延 $x$ 方向和 $y$ 方向的斜率。所以从某点 $(x_0, y_0)$ 延 $x$ 方向移动一个微小量 $\Delta x$，假设曲面平滑，则函数值增加

\begin{equation} \Delta f \approx \frac{\partial f}{\partial x} \Delta x~, \end{equation}

写成微分关系就是

\begin{equation} \,\mathrm{d}{f} = \frac{\partial f}{\partial x} \,\mathrm{d}{x} \qquad (y\, \text{不变})~. \end{equation}

2. 通用函数名

　　物理中常常会出现一种容易混淆的情况，就是当一个因变量可以有几套自变量（例如上面的 $z(u,v)$ 和 $z(x,y)$）时，通常直接用因变量（$z$）作为函数名而另外不定义函数名（$f$）。然而 $z(u,v)$ 与 $z(x,y)$ 中的 $z$ 并不是同一个函数。以下举例说明

例 3　

　　在二维直角坐标系中，定义一个曲面的方程为

\begin{equation} z=f(x,y)=x^2+y^2+2x~, \end{equation}

而若用极坐标的方程描述该曲面，则函数变为

\begin{equation} z = g(r,\theta) = f(r\cos \theta, r\sin \theta ) = r^2 + 2r\cos \theta~. \end{equation}

但许多物理书为了方便并不用 $f$ 和 $g$ 区分两个不同的函数，而是使用 $z(x,y)$ 表示式 6 和 $z(r,\theta)$ 表示式 7 。这样后者就有可能被误解为

\begin{equation} z(r,\theta) = r^2+\theta^2+2r \quad \text{(错)}~. \end{equation}

这就需要从语境中判断是否使用了通用函数名¹。

　　使用通用函数名时，要注意从语境中判断偏导数使用的是哪一套变量，例如 $ \partial z/\partial x $ 一般默认使用 $z(x,y)$ 求偏导，即把 $y$ 看成常数；$ \partial z/\partial r $ 一般默认使用 $z(r,\theta)$ 求偏导，即把 $\theta$ 看成常数。或者为了明确起见可以分别把两种情况记为式 1 中的最后一种形式

\begin{equation} \left( \frac{\partial z}{\partial x} \right) _y~, \qquad \left( \frac{\partial z}{\partial r} \right) _\theta~. \end{equation}

这样，把求偏导的变量和括号外的变量就是函数的自变量。

　　再看一种更复杂的情况，如

\begin{equation} \left( \frac{\partial z}{\partial x} \right) _\theta~. \end{equation}

按照上述定义，应该是仅用 $x$ 和 $\theta$ 表示 $z$，然后求偏导。考虑极坐标系和直角坐标系的转换（子节 1 ），有 $y=x\tan\theta$，代入式 6 得

\begin{equation} z(x,\theta) = x^2(1+\tan^2 \theta) + 2x~, \end{equation}

现在再对 $x$ 求偏导即可（过程略）。

3. 高阶偏导

　　与一元函数的高阶导数类似，多元函数也可以求高阶偏导数，不同的是，由于每求一次偏导都需要指定对哪个变量。例如二元函数 $f(x,y)$ 的二阶偏导有：

\begin{equation} \frac{\partial^{2}{f}}{\partial{x}^{2}} ~, \qquad \frac{\partial^2 f}{\partial x \partial y} ~, \qquad \frac{\partial^2 f}{\partial y \partial x} ~, \qquad \frac{\partial^{2}{f}}{\partial{y}^{2}} ~. \end{equation}

若高阶偏导的分母中出现不止一个变量，我们就称其为混合偏导。混合偏导的一个重要性质就是当函数的任意混合偏导均在某点 $M_0$ 连续时，偏导的顺序可以任意改变，例如上式中有 $ \partial^2 f/\partial x \partial y = \partial^2 f/\partial y \partial x $。
以二元函数 $z=f(x,y)$ 为例，证明其混合偏导 $f_{xy}$ 和 $f_{yx}$ 在 $M_0(x_0,y_0)$ 连续时，$f_{xy}|_{M_0}=f_{yx}|_{M_0}$。

未完成：这个证明不应该出现在简明微积分

证：考虑差商

\begin{equation} I=\frac{[f(x_0+\Delta x,y_0+\Delta y)-f(x_0+\Delta x,y_0)]-[f(x_0,y_0+\Delta y)-f(x_0,y_0)]}{\Delta x\Delta y}\\~. \end{equation}

设

\begin{equation} \begin{aligned} &\qquad\varphi(x)=f(x,y_0+\Delta y)-f(x,y_0)~,\\ &\qquad\psi(y)=f(x_0+\Delta x,y)-f(x_0,y)~,\\ \end{aligned} \end{equation}

那么利用微分中值定理可得

\begin{equation} \begin{aligned} &I=\frac{[f(x_0+\Delta x,y_0+\Delta y)-f(x_0+\Delta x,y_0)]-[f(x_0,y_0+\Delta y)-f(x_0,y_0)]}{\Delta x\Delta y}\\ &\ \ =\frac{\varphi(x_0+\Delta x)-\varphi(x_0)}{\Delta x\Delta y}\\ &\ \ =\frac{\varphi'(x_0+\alpha_1\Delta x)\Delta x}{\Delta x\Delta y}\\ &\ \ =\frac{f_x(x_0+\alpha_1\Delta x,y_0+\Delta y)-f_x(x_0+\alpha_1\Delta x,y_0)}{\Delta y}\\ &\ \ =f_{xy}(x_0+\alpha_1\Delta x,y_0+\alpha_2\Delta y)\qquad(0<\alpha_1,\alpha_2<1)~.\\ \end{aligned} \end{equation}

同理，将 $I$ 重新组合可以得到

\begin{equation} \begin{aligned} &I=f_{yx}(x_0+\alpha_4\Delta x,y_0+\alpha_3\Delta y)\qquad(0<\alpha_3,\alpha_4<1)~.\\ \end{aligned} \end{equation}

因此

\begin{equation} \begin{aligned} &\qquad f_{xy}(x_0+\alpha_1\Delta x,y_0+\alpha_2\Delta y)=f_{yx}(x_0+\alpha_4\Delta x,y_0+\alpha_3\Delta y)~.\\ \end{aligned} \end{equation}

利用两个混合偏导 $f_{xy}$ 和 $f_{yx}$ 在点 $(x_0,y_0)$ 连续的条件，得到

\begin{equation} \begin{aligned} &f_{xy}(x_0,y_0)=\lim_{(\Delta x,\Delta y)\to(0,0)}f_{xy}(x_0+\alpha_1\Delta x,y_0+\alpha_2\Delta y)\\ &\qquad\qquad\ =\lim_{(\Delta x,\Delta y)\to(0,0)}f_{yx}(x_0+\alpha_4\Delta x,y_0+\alpha_3\Delta y)\\ &\qquad\qquad\ =f_{yx}(x_0,y_0)~. \end{aligned} \end{equation}

1. ^ “通用函数名” 是笔者起的名字，不清楚是否有其他叫法