Matlab 解常微分方程组（ode45）

贡献者： addis

预备知识　Matlab 的函数，Matlab 画图

　　 Matlab 自带的 ode45 解算器使用成熟的变步长的 4 阶和 5 阶 Runge-Kutta 算法（该算法的简单实现详见）。

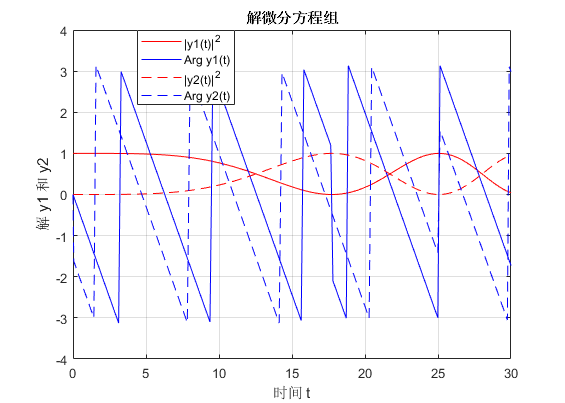
图 1：ode45_test.m 的运行结果。注意 $y_1$ 的相位在 $t=17$ 左右发生了一次反转，但此时模长为零，这代表 $y_1$ 在复平面上穿过了 $0$。$y_2$ 在 $t=25$ 穿过了 $0$。

　　下面我们演示如何用它求解一个简单的微分方程组的初值问题（结果如图 1 所示）。

\begin{equation} \left\{\begin{aligned} &\dot y_1 = - \mathrm{i} (y_1 + \alpha t y_2)~,\\ &\dot y_2 = - \mathrm{i} (\alpha t y_1 + y_2)~. \end{aligned}\right. \end{equation}

其中 $\alpha$ 为常数。为了告诉解算器我们需要求解的方程，我们要先定义一个数值函数

代码 1：odefun.m

function dydt = odefun(t, y, alpha)
    A = -1i*[1 alpha*t; alpha*t 1];
    dydt = A * y;
end

这里方程用矩阵乘法表示为

\begin{equation} \dot{ \boldsymbol{\mathbf{y}} (t)} = \boldsymbol{\mathbf{A}} (t) \boldsymbol{\mathbf{y}} (t)~. \end{equation}

表示为矩阵乘法只是为了方便而不是必须的——解算器无法看到这个函数内部是什么，只要输入某时刻的 $t$ 和 $ \boldsymbol{\mathbf{y}} (t)$ 时，输出正确的 $\dot{ \boldsymbol{\mathbf{y}} (t)}$ 即可。

　　接下来我们要把微分方程（odefun）和 $t$ 的求解范围（tspan），以及初始条件（$ \boldsymbol{\mathbf{y}} (0)$ 或 y0）告诉解算器。如果不想用两个 m 文件，可以把上面的 odefun() 函数的定义直接粘贴到 ode45_test.m 文件最后。

　　在解算器 ode45 的输出中，t 是一个 $1\times N$ 的递增数组，而 y 是一个 $2\times N$ 的矩阵，每一列对应 t 的一个值。这样就离散地表示出了函数 $ \boldsymbol{\mathbf{y}} (t_i)$。注意由于这是一个变步长解算器，t 并不是等间距的。

代码 2：ode45_test.m

function ode45_test
close all;

alpha = 0.01;  % 方程中的常数
y0 = [1; 0]; % 初始条件

% 时间跨度
tspan = [0 30];  % t 从 0 到 30

% 调用 ODE 求解器
[t, y] = ode45(@(t,y) odefun(t, y, alpha), tspan, y0);

% 绘制结果
figure;
plot(t, abs(y(:,1)).^2, 'r'); hold on; grid on;
plot(t, angle(y(:,1)), 'b');
plot(t, abs(y(:,2)).^2, 'r--');
plot(t, angle(y(:,2)), 'b--');
title('解微分方程组');
xlabel('时间 t');
ylabel('解 y1 和 y2');
legend({'|y1(t)|^2', 'Arg y1(t)', '|y2(t)|^2', 'Arg y2(t)'});
end