刘维尔定理（热力学与统计物理）

                     

贡献者： int256; addis

预备知识　相空间

　　 $(q, p)$ 空间（广义坐标、广义动量）称为相空间，复杂系统的所有系综看成多维相空间中的流体，每个具体系统的状态是相空间中的一点，随时间变化。跟随一点时，周围密度不随时间变化。

　　 $t$ 等于零时在相空间中取一块小区域，具有边界 $\mathcal B$。可以证明随着时间变化，虽然边界开始变形，但边界两边的点不会跨越边界。也可以证明，这个区域的体积始终保持不变。

　　 具体的，刘维尔定理（Liouville theorem 或 Liouville's theorem）可以表述为： 系综的概率密度 $\rho(q_i, p_i, t)$（等价于 代表点密度/相点密度 $\widetilde \rho(q_i, p_i, t)$）在运动中保持不变，即

\begin{equation} \frac{\mathrm{d}{\rho}}{\mathrm{d}{t}} = \frac{\mathrm{d}{\widetilde{\rho}}}{\mathrm{d}{t}} = 0 ~. \end{equation}

　　 这里的系综可以理解为是性质、结构与所研究系统完全相同，但互相独立、各自处于某微观状态的大量假想系统的集合。相空间中的相点遵循哈密顿正则方程移动。定理 式 1 中使用全微分而非偏微分代表观测的密度 “随相点一起移动”。式中的 $\rho$ 总正比于 $\widetilde \rho$。

图
图 1：代表点与研究的代表点密度随时间变化

　　 刘维尔定理的一个最直接推论是，如果开始时相空间中这种流体的密度处处相同，那么接下来在任意时刻 $t$，流体密度仍然处处相同。

　　 在这样的流体里面随机抽取一个点，那么这个点几乎肯定处于平衡态。热力学第二定律就是在这个 “几乎肯定” 上成立的。

　　 下面考虑刘维尔定理的一个经典证明：

　　 设自由度为 $s$ 的 $2s$ 维相空间（$q_i$、$p_i$ 各有 $s$ 维）的某处体元 $ \,\mathrm{d}{\Omega} = \mathrm{d}^{s}{p_i} \mathrm{d}^{s}{q_i}$ 内有一些相点，有相点密度 $\widetilde \rho(q_i, p_i, t)$。考虑这些相点随时间变化 $t \rightarrow t + \,\mathrm{d}{t} $，各自沿由正则运动方程（哈密顿正则方程）规定的轨道各自独立运动（每个相点代表系综中的一个 “系统”，系统间互相独立）： $$ \begin{aligned} t &\rightarrow t+ \,\mathrm{d}{t} , \\ q_i(t) &\rightarrow q_i(t+ \,\mathrm{d}{t} ) = q_i + \dot q_i \,\mathrm{d}{t} , \\ p_i(t) &\rightarrow p_i(t+ \,\mathrm{d}{t} ) = p_i + \dot p_i \,\mathrm{d}{t} , \\ \,\mathrm{d}{\Omega} &\rightarrow \,\mathrm{d}{\Omega} ', \\ \widetilde \rho(q_i, p_i, t) &\rightarrow \widetilde \rho(q_i + \dot q_i \,\mathrm{d}{t} , p_i + \dot p_i \,\mathrm{d}{t} , t + \,\mathrm{d}{t} ), \end{aligned}~~ $$ 考虑 $ \,\mathrm{d}{\widetilde{\rho}} = \widetilde{\rho}(q_i + \dot q_i \,\mathrm{d}{t} , p_i + \dot p_i \,\mathrm{d}{t} , t + \,\mathrm{d}{t} ) - \widetilde{\rho}(q_i, p_i, t)$，这就使得有：

\begin{equation} \,\mathrm{d}{\widetilde \rho} = \frac{\partial \widetilde \rho}{\partial t} \,\mathrm{d}{t} + \sum_{i=1}^{s}\left( \frac{\partial \widetilde \rho}{\partial q_i} \dot q_i + \frac{\partial \widetilde \rho}{\partial p_i} \dot p_i\right) \,\mathrm{d}{t} ~, \end{equation}
分别考虑这式的两项。

　　 首先看第一项 $ \frac{\partial \widetilde \rho}{\partial t} $，这代表了在固定位置的相点密度的时间变化率，也就是在 $ \,\mathrm{d}{\Omega} $ 内的相点的数量在 $ \,\mathrm{d}{t} $ 时间内的变化。这是相点沿着各自在相空间内的轨道运动导致的，本身在 $ \,\mathrm{d}{\Omega} $ 内的某些相点在 $ \,\mathrm{d}{t} $ 时间后运动离开 $ \,\mathrm{d}{\Omega} $，而某些不在 $ \,\mathrm{d}{\Omega} $ 内的相点在 $ \,\mathrm{d}{t} $ 时间后运动到 $ \,\mathrm{d}{\Omega} $ 内。故，$ \,\mathrm{d}{t} $ 内 $ \,\mathrm{d}{\Omega} $ 内相点增加 $ \frac{\partial \widetilde \rho}{\partial t} \,\mathrm{d}{t} \,\mathrm{d}{\Omega} $ 个。

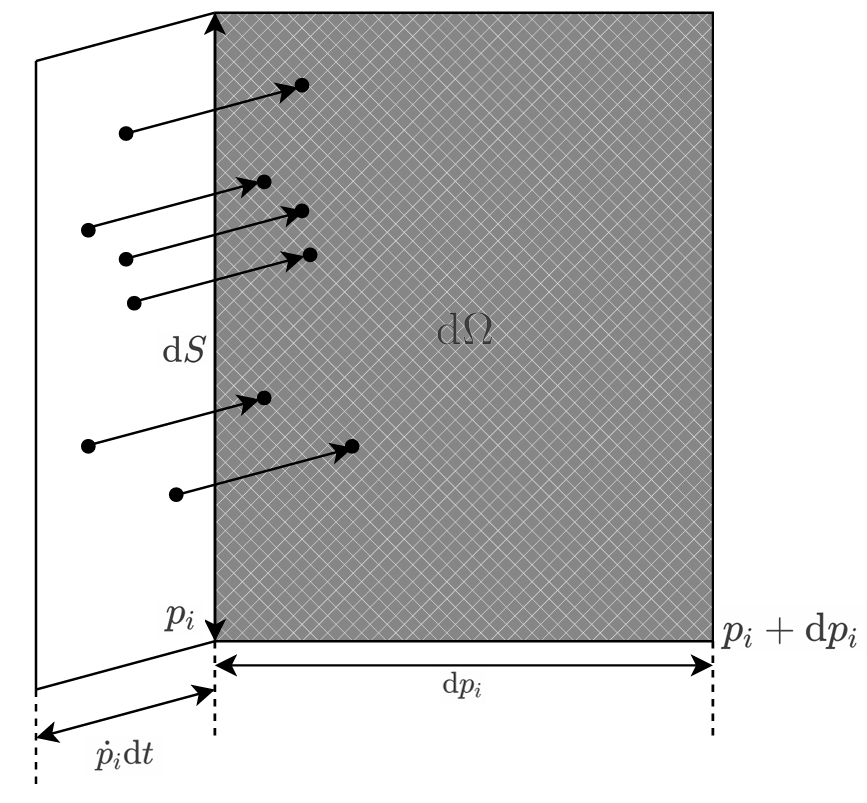
　　 而 $ \,\mathrm{d}{\Omega} = \,\mathrm{d}{} ^s q_i \cdot \,\mathrm{d}{} ^s p_i$ 是由 $2s$ 对平面围成的：$q_i$ 与 $q_i + \,\mathrm{d}{q} _i$ 共 $s$ 个，$p_i$ 与 $p_i + \,\mathrm{d}{p} _i$ 共 $s$ 个。不失一般性的，考虑其中任意一对（超）平面，不妨考虑 $p_i$ 与 $p_i+ \,\mathrm{d}{p} _i$。设 $ \,\mathrm{d}{\Omega} = \,\mathrm{d}{p} _i \times \,\mathrm{d}{S} $。

图
图 2：$ \,\mathrm{d}{t} $ 时间内通过 $p_i$ 处的 $ \,\mathrm{d}{S} $ 平面进入 $ \,\mathrm{d}{\Omega} = \,\mathrm{d}{t} \times \,\mathrm{d}{S} $ 区域的示意图

　　 相点的箭头方向是各相点速度在 $\dot p_i$ 方向上的投影，因为我们只考虑 $p_i$ 方向上的变化。

　　 首先考虑流入 $ \,\mathrm{d}{\Omega} $ 区域的点，应当在 $\left(\dot p_i \,\mathrm{d}{t} \right) \times \,\mathrm{d}{S} $ 这个（超）柱体内。“底面积” 为 $ \,\mathrm{d}{S} $，高 $\dot p_i \,\mathrm{d}{t} $，这区域内有相点 $\widetilde \rho \left(\dot p_i \,\mathrm{d}{t} \,\mathrm{d}{S} \right)$ 个。类似的，流出的点从 $p_i + \,\mathrm{d}{p} _i$ 位置，故流出相点 $$ \left[\widetilde \rho \left(\dot p_i \,\mathrm{d}{t} \,\mathrm{d}{S} \right)\right]_{p_i + \,\mathrm{d}{p} _i} = \left[ \left. \left(\widetilde\rho \dot p_i\right) \right\rvert _{p_i} + \left. \frac{\partial \left(\widetilde\rho \dot p_i\right)}{\partial p_i} \right\rvert _{p_i} \,\mathrm{d}{p} _i \right] \,\mathrm{d}{t} \,\mathrm{d}{S} ~~ $$ 个。将这式与 $\widetilde \rho \left(\dot p_i \,\mathrm{d}{t} \,\mathrm{d}{S} \right)$ 相减得到净流入 $ \,\mathrm{d}{\Omega} $ 区域的相点数为

\begin{equation} - \frac{\partial \left(\widetilde \rho p_i\right)}{\partial p_i} \,\mathrm{d}{t} \,\mathrm{d}{\Omega} ~~ \end{equation}
个。而这对于 $q_i$ 是等价的。故共净流入相点
\begin{equation} \frac{\partial \widetilde \rho}{\partial t} \,\mathrm{d}{t} \,\mathrm{d}{\Omega} = - \sum_{i} \left( \frac{\partial \left(\widetilde \rho \dot p_i\right)}{\partial p_i} + \frac{\partial \left(\widetilde \rho \dot q_i\right)}{\partial q_i} \right) \,\mathrm{d}{t} \,\mathrm{d}{\Omega} ~~ \end{equation}
个。故有
\begin{equation} \frac{\partial \widetilde \rho}{\partial t} = -\sum_{i} \left( \frac{\partial \left(\widetilde \rho \dot p_i\right)}{\partial p_i} + \frac{\partial \left(\widetilde \rho \dot q_i\right)}{\partial q_i} \right) ~. \end{equation}
将这结果代回式 2 ，可以得到
\begin{equation} \frac{\mathrm{d}{\widetilde \rho}}{\mathrm{d}{t}} = -\widetilde \rho \sum_{i} \left( \frac{\partial \dot q_i}{\partial q_i} + \frac{\partial \dot p_i}{\partial p_i} \right) ~, \end{equation}
再考虑哈密顿正则运动方程，引入哈密顿量 $H$，就可以得到证明：
\begin{equation} \frac{\mathrm{d}{\widetilde \rho}}{\mathrm{d}{t}} = -\widetilde \rho \sum_{i} \left( \frac{\partial }{\partial q_i} \frac{\partial H}{\partial p_i} - \frac{\partial }{\partial p_i} \frac{\partial H}{\partial q_i} \right) = 0 ~. \end{equation}

推论 1　泊松括号表达下的刘维尔定理

　　 若引入泊松括号还可以将式 7 改写为：

\begin{equation} \frac{\partial \widetilde \rho}{\partial t} + \{\widetilde \rho, H\} = \frac{\partial \rho}{\partial t} + \{\rho , H\} = 0 ~, \end{equation}
这正是刘维尔定理的另一表达形式。这使得我们可以发现，刘维尔定理的成立条件是系统为保守系（哈密顿量 $H$ 不显含时），并且系统在我们研究的时间内不受外界作用。

　　 可以发现，刘维尔定理是纯粹由经典力学得到的推论，证明只需要运用到哈密顿正则运动方程。

　　 值得一提的，如果外界作用满足绝热近似，而且可以用势场的形式表达，那么刘维尔定理仍然适用。

推论 2　系综的概率分布函数与连续性方程

　　 考虑在式 5 的基础上引入速度与 $\nabla$ 算子

\begin{equation} \begin{aligned} \boldsymbol{\mathbf{v}} &\equiv (\dot q_1, \dot q_2, \dots, \dot q_s, \dot p_1, \dot p_2, \dots, \dot p_s), \\ \nabla &\equiv ( \frac{\partial }{\partial q_1} , \frac{\partial }{\partial q_2} , \dots, \frac{\partial }{\partial q_s} , \frac{\partial }{\partial p_1} , \frac{\partial }{\partial p_2} , \dots, \frac{\partial }{\partial p_s} ) ~. \end{aligned} \end{equation}
这里 $ \boldsymbol{\mathbf{v}} $ 为相点在相空间内的速度，$\nabla$ 是这相空间的 nabla 算子。则可以将式 5 改写为连续性方程（式 3 ）的形式：
\begin{equation} \frac{\partial \widetilde \rho}{\partial t} + \nabla \cdot \left( \widetilde \rho \boldsymbol{\mathbf{v}} \right) = 0 ~. \end{equation}
其中 $\nabla \cdot$ 是这相空间的梯度算符。这式代表相点数守恒。

                     

© 小时科技 保留一切权利