二项式定理(高中)
贡献者: jingyuan; addis
1. 定义
\begin{equation}
(a + b)^n = C_n^0a^n + C_n^1a^{n- 1}b + C_n^2a^{n- 2}b^2 + \cdots + C_n^ra^{n-r}b^r + \cdots + C_n^nb^n \qquad (n\in N_{+})~.
\end{equation}
这个公式所表示的规律叫做二项式定理(binomial theorem), 等式右边的多项式叫做 $(a+b)^n$ 的二项展开式(binomial expansion),它一共有 $n+1$ 项,其中各项系数 $C_n^r(r = 0, 1, \cdots, n)$ 叫做展开式的二项式系数(binomial coefficient)。展开式中的 $C_n^ra^{n-r}b^r$ 项叫做二项展开式的通项,通项是展开式的第 $r+1$ 项。
注意:二项式系数不是项的系数。
2. 推导
我们在初中时就学过平方和公式,$(a+b)^2 = a^2 + 2ab + b^2$ 显然这就是一个二项式,我们先从这里开始研究。
\begin{equation}
\begin{aligned}
(a+b)^2 &= a(a + b) + b(a + b)\\
&= a^2 + ab + ab + b^2\\
&= a^2 + 2ab + b^2~,
\end{aligned}
\end{equation}
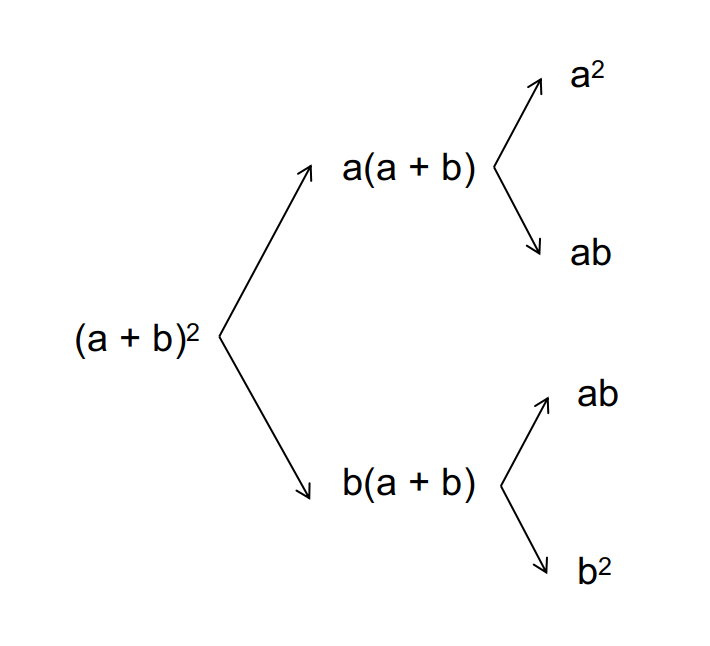
我们将式 2 的过程图形化。
图 1:平方和的运算过程
我们会发现在树状图的分支会延伸到同一深度,且各项的次数相同,在树状图延伸的过程中,每一项都会有 $a$ 和 $b$ 两种情况,那么二项式系数的问题就转换成了排序问题,对于 $a^rb^{n-r}$,$a$ 和 $b$ 有多少种排序方式。
注意:这里不是排列,不符合排列定义
此时我们有 $n-r$ 个 $a$ 和 $r$ 个 $b$ 我们对其进行编号,将其转化为排列问题
$a_1,a_2,\cdots,a_{n-r};b_1,b_2,\cdots,b_r~.$
则共有 $A_n^n$ 种排列,
之后我们排除掉重复的排列,
\begin{equation}
\begin{aligned}
\frac{A_n^n}{A_r^rA_{n-r}^{n-r}} &= \frac{n!}{r!(n-r)!}\\
&= \frac{A_n^r}{A_r^r}\\
&= C_n^r~.
\end{aligned}
\end{equation}