磁场（高中）

贡献者： kahoyip

预备知识 1　静电场

1. 磁场

　　具有磁性的物质叫做磁体，能吸引铁、钴、镍等物质。磁体上磁性最强的部分叫做磁极，分北极（$\mathrm N$）和南极（$\mathrm S$），磁极不能单独存在。

　　磁极之间的作用规律为：同名磁极相互排斥，异名磁极相互吸引。

　　磁场是磁体或电流周围存在的一种看不见、摸不着的特殊物质。磁体与磁体、磁体与电流、电流与电流之间都存在相互作用，统称为磁相互作用，这种相互作用是通过磁场发生的。

　　磁场中某点磁场方向的表述：

小磁针北极受磁场力的方向；
小磁针静止时北极所指的方向；
磁感线某点的切线方向；
磁感应强度的方向。

磁感线

　　与电场线类似，为了形象地描述磁场，在磁场中画出一系列有方向的假想曲线，曲线上每一点的切线方向都跟该点的磁场方向相同，这样的曲线叫做磁感线（也叫做磁力线）。

　　在磁体的外部，磁感线从北极到南极，在磁体内部则从南极到北极。

　　磁感线的疏密程度反映了磁场的强弱，磁感线密的位置磁场强，磁感线疏的位置磁场强。

地磁场

　　地球是个巨大的磁体，在地球周围的空间存在着磁场，这个磁场叫做地磁场。地磁北极在地理南极附近，地磁南极在地理北极附近，地磁极和地理极并不重合，它们之间的夹角叫做磁偏角。

2. 磁现象

电流的磁效应

　　丹麦物理学家奥斯特通过实验发现，通电导体周围存在磁场，且磁场的方向跟电流的方向有关，这一现象叫做电流的磁效应。

分子电流假说

　　法国物理学家安培提出了分子电流假说：在原子、分子等物质为例的内部，存在一种环形电流——分子电流，分子电流使每个物质微粒都成为一个微小的磁体。如一根未被磁化的铁棒，其内部的各分子电流都是杂乱无章的，对外无磁性；当分子电流受到外部磁场的作用时，各分子电流的取向趋于规则，铁棒被磁化，对外显现出磁性；在高温下，铁棒的分子热运动变得剧烈，分子电流又变得杂乱无章，铁棒失去磁性（消磁）。

3. 磁感应强度

　　 磁感应强度是用于描述磁场的强弱和方向的物理量，用 $ \boldsymbol{\mathbf{B}} $ 表示。

　　对于一个磁场中的某个点，运动的点电荷经过该点时，若点电荷的速度与磁场方向平行，磁场对该电荷没有力的作用；若点电荷的速度与磁场垂直时，磁场对该电荷的作用力最大，这个作用力的大小与电荷的运动速度和电荷量的乘积成正比。

　　磁感应强度可以用上述三个物理量来定义：

\begin{equation} B=\frac{F}{qv}~. \end{equation}

　　即磁场中某点的磁感应强度大小等于电荷以垂直于磁场方向的速度通过该点时所受的力与该电荷的电荷量和速度的乘积之比。

　　在国际单位制中，磁感应强度的单位是特斯拉（简称特），符号为 $\mathrm{T}$，由式可知： $$1\mathrm{T}=1\mathrm{N}\cdot ( \mathrm{C \cdot m \cdot s^{-1} } )^{-1}= 1 \mathrm{N} \cdot ( \mathrm{A} \cdot \mathrm{m})^{-1}~.$$

　　需要注意，磁场中某点的磁感应强度的大小和方向是由磁体决定的，跟经过该点的电荷的速度和电荷量无关。

　　磁感应强度是一个矢量，磁场中某点的磁感应强度的方向为小磁针在该点静止时 $\mathrm{N}$ 极所指的方向。

　　若磁场中各点的磁感应强度大小和方向都相同，则这个磁场叫做匀强磁场。

磁通量

　　在磁感应强度为 $ \boldsymbol{\mathbf{B}} $ 的匀强磁场中，有一个与磁场方向垂直且面积为 $S$ 的平面，磁感应强度大小和面积的乘积叫做穿过这个面积的磁通量（简称磁通），用 $\Phi$ 表示，即

\begin{equation} \Phi = BS~. \end{equation}

　　在国际单位制中，磁通量的单位是韦伯，用 $\mathrm{Wb}$ 表示，$1\mathrm{Wb}=1\mathrm{T\cdot m^2}$。

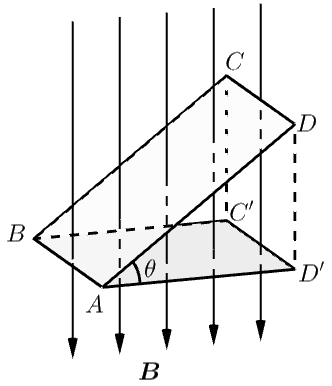
　　若磁场方向与所研究的平面不垂直（如图 1 ），且该平面与磁场方向的垂面所成角度为 $\theta$，则穿过该平面的磁通量为

\begin{equation} \Phi = BS\cos\theta~. \end{equation}

　　 $S\cos\theta$ 为所研究平面在垂直于磁场方向的投影面积。

图 1：磁通量示意图

　　磁通量是一个标量，其正、负与所研究平面的正面的规定有关，我们可看作是穿过该平面的磁感线的净条数（穿入为正，穿出为负，求代数和）。那么对于磁场中任意一个闭合的曲面（考虑一个球面），磁感线从一处穿入就必从另一处穿出，因此穿过该闭合曲面的磁感线净条数为零，即磁通量为零。

4. 安培力

　　磁场对通电导线的作用力被称为安培力。

安培力的大小

　　在磁感应强度为 $ \boldsymbol{\mathbf{B}} $ 的匀强磁场中，通电直导线的电流为 $I$，长度为 $L$，当直导线（电流方向）与磁场方向垂直时，通电直导线所受的安培力大小为 $F=BIL$；当直导线与磁场方向平行时，直导线所受的安培力大小为零；当直导线与磁场方向所成角度为 $\theta$ 时，直导线所受的安培力大小为 $F=BIL\sin\theta$。归纳起来，一般情况下安培力的大小可表示为

\begin{equation} F=BIL\sin\theta~. \end{equation}

　　 $L\sin\theta$ 可看作是直导线在垂直于磁场方向上的等效长度，对于弯曲的导线，这个等效长度为导线始端到末端的连线长。

安培力的方向

　　安培力的方向可用右手定则¹或左手定则判断，两者的使用方式不同，需注意其区别及联系，根据个人习惯及实际情况合理使用。

右手定则：伸直右手，使拇指和其他四指垂直，并且五指在同一平面内，四指指向电流方向，当四指以小于 $180^\circ$ 的角度弯向磁场方向时，拇指所指的方向就是安培力的方向。
左手定则：当电流方向垂直于磁场方向时，伸直左手，使拇指和其他四指垂直，并且五指与手掌都在同一平面内，让磁场方向指向掌心，四指指向电流方向，此时拇指所指的方向就是安培力的方向。

5. 洛伦兹力

　　磁场对运动电荷的作用力被称为洛伦兹力。

洛伦兹力的大小

　　带电量为 $q$ 的电荷在磁感应强度为 $ \boldsymbol{\mathbf{B}} $ 的匀强磁场中运动，当电荷的速度 $ \boldsymbol{\mathbf{v}} $ 与磁感应强度 $ \boldsymbol{\mathbf{B}} $ 垂直时，电荷所受的洛伦兹力大小为 $F=qvB$；当电荷的运动方向与磁场方向在同一直线上时，电荷所受的洛伦兹力为零；当电荷的速度与磁感应强度的夹角为 $\theta$ 时，电荷所受的洛伦兹力大小为 $F=qvB\sin\theta$。归纳起来，运动电荷所受的洛伦兹力大小为

\begin{equation} F=qvB\sin\theta~. \end{equation}

洛伦兹力的方向

　　洛伦兹力的方向可用左手定则或右手定则判断。

左手定则：当电荷运动方向与磁场方向垂直时，伸直左手，使拇指和其他四指垂直，并且五指与手掌都在同一平面内，让磁场方向指向掌心，四指指向正电荷的运动方向（对于负电荷，四指指向负电荷运动的反方向），此时拇指所指的方向就是洛伦兹力的方向。
右手定则：伸直右手，使拇指和其他四指垂直，并且五指在同一平面内，四指指向正电荷的运动方向（对于负电荷，四指指向负电荷运动的反方向），当四指以小于 $180^\circ$ 的角度弯向磁场方向时，拇指所指的方向就是洛伦兹力的方向。

　　洛伦兹力的方向总是与电荷运动的方向垂直，因此洛伦兹力对运动电荷不做功（不改变运动速度和动能的大小），只改变电荷的运动方向。

6. 带电粒子在匀强磁场中的运动

预备知识 2　圆周运动

　　带电粒子在磁场中的运动是个比较复杂的问题，这里先不考虑带电粒子的重力，并假设它的带电量为 $q$，质量 $m$，在匀强磁场 $ \boldsymbol{\mathbf{B}} $ 中以初速度 $ \boldsymbol{\mathbf{v}} $ 运动。

若磁场方向与初速度方向平行，带电粒子不受洛伦兹力的作用，做匀速直线运动。
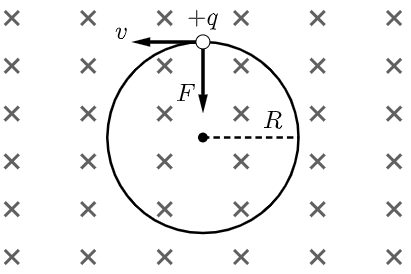
若磁场方向与初速度方向垂直，带电粒子仅受到洛伦兹力的作用，在垂直于磁场的平面做匀速圆周运动，此时由洛伦兹力提供向心力，则有
\begin{equation} qvB=\frac{mv^2}{R}~. \end{equation}

图 2：圆周运动
结合圆周运动相关知识，运动半径、周期和角速度分别为
\begin{equation} R=\frac{mv}{Bq}~, \quad T=\frac{2\pi m}{Bq}~, \quad \omega=\frac{Bq}{m}~. \end{equation}
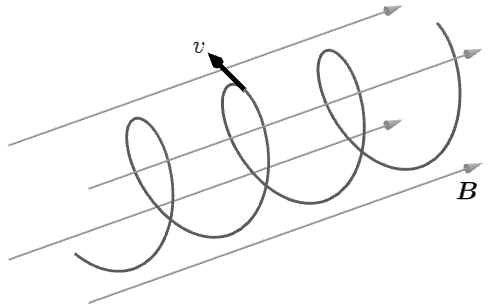
若磁场方向与初速度方向所成角为 $\theta$，我们可以把初速度 $v$ 分解成平行于磁场 $v \cos \theta$ 和垂直于磁场的 $v \sin \theta$ 两个分量，在平行于磁场的方向上带电粒子做速度大小为 $v \cos \theta$ 的匀速直线运动，而在垂直于磁场的方向上带电粒子以 $v \sin \theta$ 做匀速圆周运动，其实际轨迹是一条螺旋线。

图 3：螺旋线运动

1. ^ 参考：右手定则