群论中的证明和习题解答

例 1　对换和逆序数

　　 问题来源请见例 2 。

例 2　迷向子群

　　 问题来源请见习题 1 。

　　 已知群 $G$ 作用在集合 $X$ 上，且对于 $x\in X$ 有 $G$ 的子集 $F_x=\{g\in G|g\cdot x=x\}$。

　　 那么 $\forall g\in F_x$，$(g^{-1}g)\cdot x=e\cdot x=x$。又因为 $g\cdot x=x$，所以 $g^{-1}\cdot x=g^{-1}\cdot(g\cdot x)=(g^{-1}g)\cdot x=x$。

　　 因此，$\forall g_1, g_2\in F_x$，有 $(g_1^{-1}g_2)\cdot x=g_1^{-1}\cdot x=x$，也就是说，$(g_1^{-1}g_2)\in F_x$。根据判别式定理 1 ，$F_x$ 构成 $G$ 的子群。

例 3　Burnside 引理

　　 首先转写一个表达：$\sum_{g\in G}|X^g|=$“满足 $g\cdot x=x$ 的 $(g, x)$ 数量”$=\sum_{x\in X}|F_x|$。

　　 由推论 3 ，$\sum_{x\in X}|F_x|=\sum_{x\in X} |G|/|O_x|=|G| \sum_{x\in X} 1/|O_x|$

　　 现在关键是 $\sum_{x\in X} 1/|O_x|$ 是多少。显然，$\sum_{x\in O_x} 1/|O_x|=1$，也就是说 $1/|O_x|$ 在每一个 $O_x$ 上求和的结果是 $1$，那么它在整个 $X$ 上求和的结果，刚好就是所有轨道的数量 $|\{O_x|x\in X\}|$。

　　 把以上结果整合，我们有：$\sum_{g\in G}|X^g|=|G|\cdot|\{O_x|x\in X\}|$。

例 4　Burnside 引理的应用

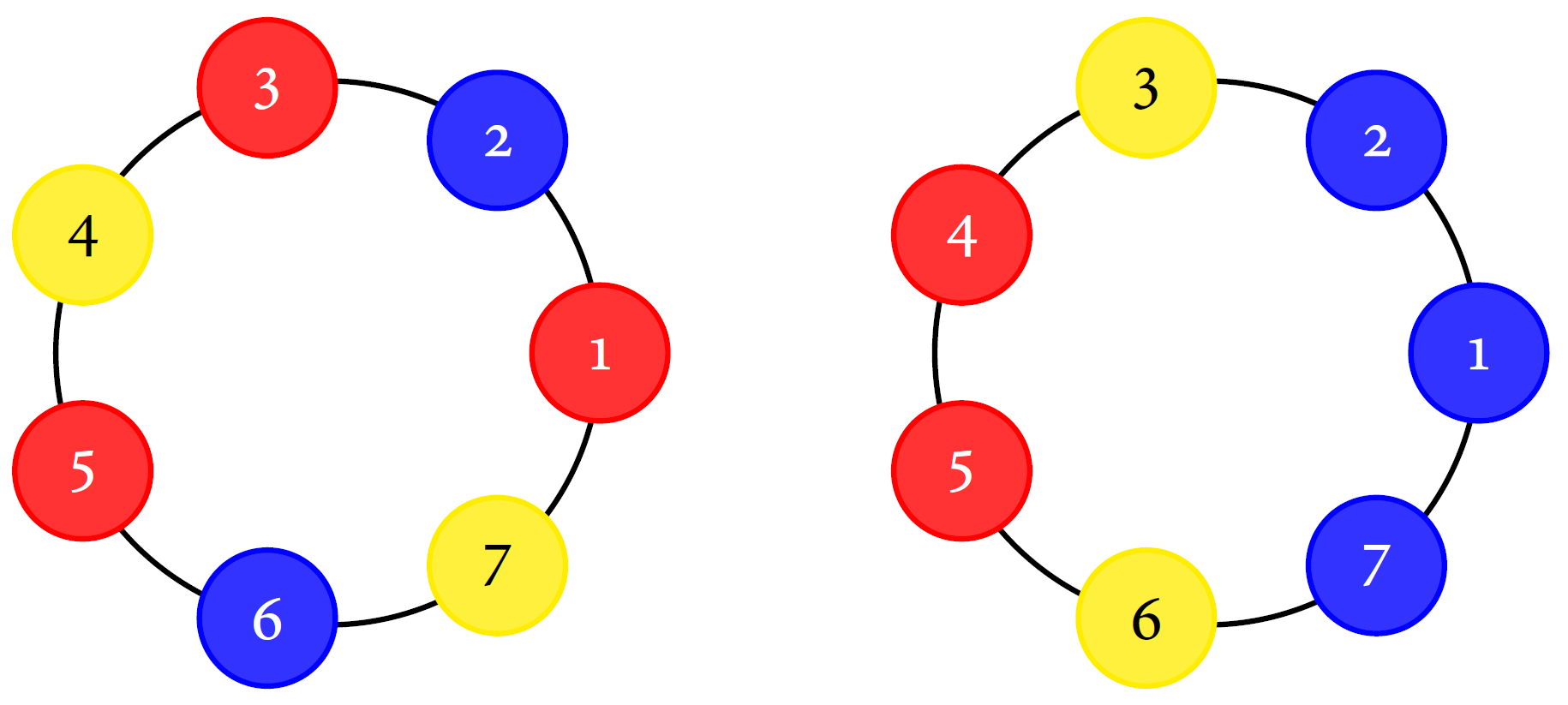
　　 一堆珍珠有 $k$ 种颜色，且每种颜色的珍珠都足够多。其中取 $n$ 个珍珠串成一个手环，试问一共可以组成多少种不同的手环？旋转或翻转可以重合的情况算作一种。

　　 我们给每个珍珠从 $1$ 到 $n$ 编号。设 $F=\{f_1,...,f_k\}$ 是不同颜色的集合，$X=F^n$ 是在固定顺序下，手环的所有颜色排列方案。显然在顺序固定情况下有 $k^n$ 种可能性，对应的是 $|X|=k^n$。我们现在要做的，是把所有旋转或翻转可以重合的情况，只保留记作一种。这等价于二面体群 $D_{2n}$ 作用在集合 $X$ 上。对于任意元素 $x_1,x_2\in X$，$x_1$ 在 $D_{2n}$ 作用下得到 $x_2$，等价于 $x_1,x_2$ 位于同一个轨道。而我们想求的去重复的不同排列数，也正是全部轨道的数量。

　　 有了这样的思路，我们应用 Burnside 引理：首先对 $D_{2n}=\{e,d,...,d^{n-1},s,ds,...,d^{n-1}s\}$ 中的每个元素，计算其不动点的数量。（其中 $d$ 表示旋转，$s$ 表示翻转）

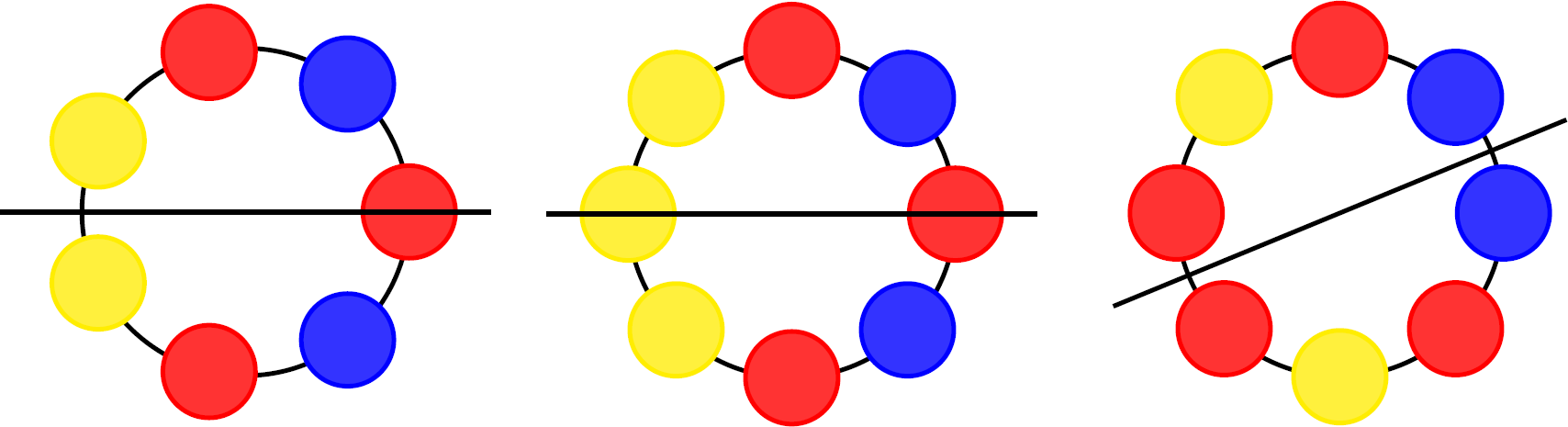
　　 对于 $n$ 种翻转，当 $n$ 为奇数时，翻转轴一定经过一颗珍珠。对于这颗珍珠，以及翻转轴其中一侧的珍珠，一共有 $(n+1)/2$ 个，我们可以随意为它们选择颜色，从而得到该作用下 $k^\frac{n+1}{2}$ 个不动点。类似情况，当 $n$ 偶数时，有一半情况翻转轴经过两颗珍珠，一共有 $k^{\frac{n}{2}+1}$ 个不动点，另一半情况翻转轴不经过珍珠，一共有 $k^{\frac{n}{2}}$ 个不动点。

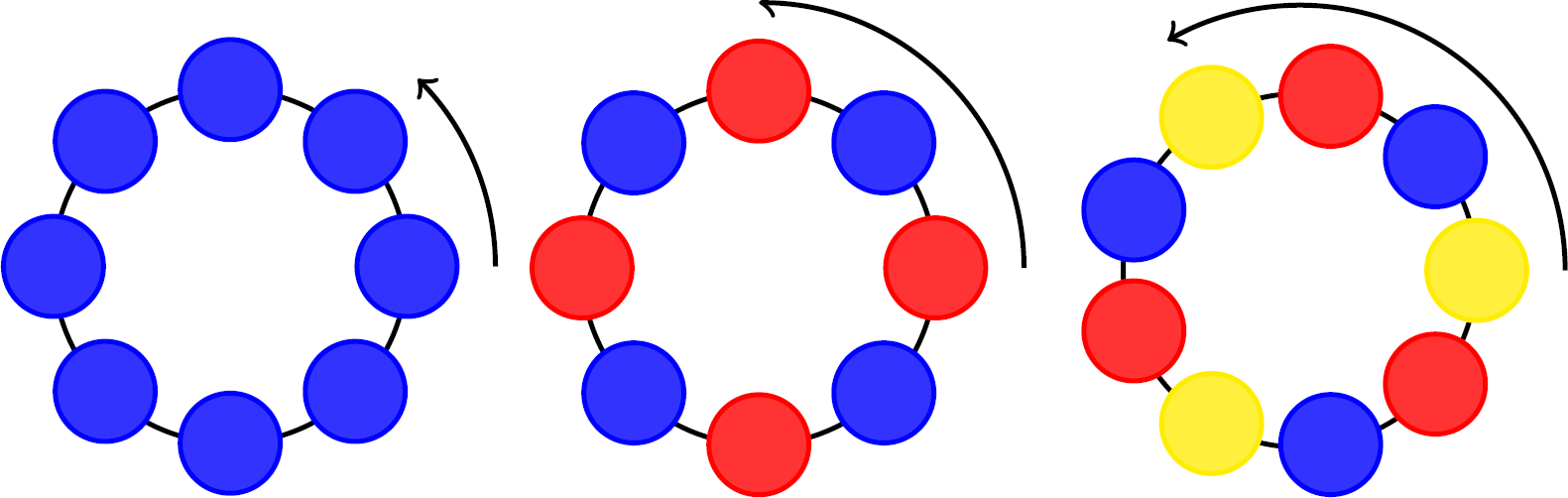
　　 对于 $n$ 种旋转的情况(我们把保持不变的操作算作旋转 $0$ 次，当然也可以看成旋转 $n$ 次，即 $e=d^0$ 和 $d^n$ 表示同一种操作)。易见，当旋转一次时，当且仅当所有珍珠为同一颜色时，旋转后的颜色才会和旋转前重合。一共可能的颜色有 $k$ 种，对应着 $k$ 个不动点。对于一般情况 $d^r$，即旋转 $r$ 次，$1\le r\le n$，令 $m=\gcd(n,r)$。那么有 $k^m$ 种可能，随意为编号从 $1$ 到 $m$ 颗珍珠选择颜色，之后需要按照相同的样式，重复 $n/m$ 次直到刚好填满全部珍珠。于是我们得到旋转 $r$ 次时，不动点的个数为：$k^{\gcd(n,r)}$

　　 最终，我们可以通过 Burnside 引理计算出轨道数，即制作不同手环的种类数。

　　 例如，当 $n=4$，$k=2$ 时，一共有 $\frac{1}{8}\big((8+4+8+4)+(16+2+4+2)\big)=6$ 种，以及当 $n=5$，$k=3$ 时，一共有 $\frac{1}{10}\big((27+27+27+27+27)+(243+3+3+3+3)\big)=39$ 种。

例 5　自由群的一般性质

　　 问题来源请见定理 2

　　 设集合 $S$ 到群 $G$ 上有一个集合间的映射 $f$。我们来构造一个 $\varphi: F(S)\rightarrow G$ 的同态。

　　 首先，由于 $\varphi$ 是 $f$ 的扩张，因此要定义 $\forall s\in S, \varphi(s)=f(s)$。

　　 其次，由于 $\varphi$ 应为一个群同态，因此要定义 $\forall s_i\in S, \varphi({s_1s_2s_3\cdots})=\varphi(s_1)\varphi(s_2)\varphi(s_3)\cdots$。同时，还需要有 $\varphi(s^{-1})=\varphi(s)^{-1}$。

　　 这样一来，$\varphi$ 的映射规则就确定下来了，并且容易验证它是一个群同态。因此这是唯一一个符合同态条件的扩张。