高斯光束
贡献者: addis
- 本文处于草稿阶段。
- 本文缺少预备知识,初学者可能会遇到困难。
- 翻译成中文
Wave Eq.
\begin{equation}
\boldsymbol{\nabla}^2 \boldsymbol{\mathbf{E}} - \frac{1}{c^2} \frac{\partial^{2}{ \boldsymbol{\mathbf{E}} }}{\partial{t}^{2}} = 0~.
\end{equation}
\begin{equation}
\boldsymbol{\mathbf{E}} = \hat{\boldsymbol{\mathbf{\epsilon}}} E( \boldsymbol{\mathbf{r}} , t) = 2 \hat{\boldsymbol{\mathbf{\epsilon}}} U(x, y, z) \mathrm{e} ^{ \mathrm{i} (kz - \omega t)}~,
\end{equation}
\begin{equation}
2 \mathrm{i} k \frac{\partial U}{\partial z} = \frac{\partial^{2}{U}}{\partial{x}^{2}} + \frac{\partial^{2}{U}}{\partial{y}^{2}} ~.
\end{equation}
\begin{equation}
U_{mn}(x, y, z) = \frac{C}{w(z)} \exp\left[-\frac{r^2}{w^2(z)}\right] \exp\left[ \mathrm{i} k\frac{r^2}{2R(z)}\right] H_m \left[\frac{\sqrt{2}x}{w(z)} \right] H_n \left[\frac{\sqrt{2} y}{w(z)} \right] \mathrm{e} ^{- \mathrm{i} \phi_{mn}(z)}~.
\end{equation}
\begin{equation}
\phi_{mn}(z) = (m+n+1)\tan^{-1}(z/z_R)~,
\end{equation}
\begin{equation}
w(z) = w_0\sqrt{1 + z^2/z_R^2}~,
\qquad
R(z) = z + z_R^2 / z~,
\qquad
z_R = \pi w_0^2 / \lambda~,
\end{equation}
\begin{equation}
H_0 = 1 ~,\qquad H_1 = 2x~, \qquad H_2 = 4x^2 - 1~.
\end{equation}
\begin{equation}
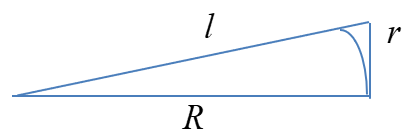
l - R = \sqrt{R^2 + z^2} - R \approx \frac{r^2}{2R}~.
\end{equation}
图 1:triangle
$TEM_{00}$ is the fundamental Gaussian mode.
In cylindrical coordinates, the basis change to Laguerre-Gauss modes $TEM_{lm}^*$
\begin{equation}
U_{lm}(r, \theta, z) = \frac{C'}{w(z)} \left[\frac{\sqrt{2}r}{w(z)} \right] ^{ \left\lvert m \right\rvert } \exp\left[-\frac{r^2}{w^2(z)}\right] \exp\left[ \mathrm{i} \frac{r^2}{2R(z)}\right] L_l^{ \left\lvert m \right\rvert } \left[\frac{2r^2}{w^2(z)} \right] \mathrm{e} ^{ \mathrm{i} m\theta} \mathrm{e} ^{- \mathrm{i} \phi_{lm}(z)}~,
\end{equation}
\begin{equation}
\phi_{lm}(z) = (2l + \left\lvert m \right\rvert + 1) \tan^{-1} (z/z_R)~.
\end{equation}