贡献者: addis; _Eden_
1本文使用原子单位制。一维定态薛定谔方程式 4 为
\begin{equation}
-\frac{1}{2m} \frac{\mathrm{d}^{2}}{\mathrm{d}{x}^{2}} \psi(x) + V(x) \psi(x) = E \psi(x)~.
\end{equation}
图 1:有限深方势阱
令势能函数为
\begin{equation}
V(x) = \begin{cases}
-V_0 \quad &(-L/2 \leqslant x \leqslant L/2)\\
0 \quad &(\text{其他})~,
\end{cases}
\end{equation}
该势能叫做
有限深势阱(finite square well)。
有限深势阱既包含连续的本征态(散射态),一定包含有限个离散的束缚态(证明见下文)。有限深势阱是研究一维散射问题的一个简单模型。在这个问题中,束缚态的 $E<0$,散射态的 $E>0$。
1. 束缚态
对于束缚态,$E<0$,而且 $E> V_{min}=-V_0$。这可以用反证法来证明:如果 $E< V_{min}$,那么由定态薛定谔方程 $\frac{ \,\mathrm{d}{^2} \psi}{ \,\mathrm{d}{x} ^2}=2m[V(x)-E]\psi$ 就会得出 $\psi$ 和它的二次导数符号相同,这种情况下波函数是不可归一化的。因此我们有 $-V_0< E<0$。
由于 $V(x)$ 是对称的,所以不失一般性,我们假设波函数是奇函数或偶函数来简化问题(式 9 )。令
\begin{equation}
\kappa = \sqrt{-2mE}, \qquad k = \sqrt{2m(E + V_0)}~.
\end{equation}
第 1,3 区间的通解为(在这个区间上 $V(x) > E$)
\begin{equation}
\psi(x) = C_1 \mathrm{e} ^{\kappa x} + C_2 \mathrm{e} ^{-\kappa x}~.
\end{equation}
为了让无穷远处波函可归一化,所以
\begin{equation}
\psi_1(x) = A \mathrm{e} ^{\kappa x}, \qquad \psi_3(x) = D \mathrm{e} ^{-\kappa x}~.
\end{equation}
第 2 区间的通解为(在这个区间上 $V(x) < E$)
\begin{equation}
\psi_2(x) = B \cos\left(k x\right) + C \sin\left(k x\right) ~.
\end{equation}
奇波函数
当波函数为奇函数时,易得 $\psi(0) = 0$ 即 $B = 0$,且 $A = -D$。再考虑 $x = L/2$ 处波函数及一阶导数连续有
\begin{equation}
\begin{aligned}
&C \sin\left(k L/2\right) = D \exp\left(-\kappa L/2\right) ~,\\
&k C \cos\left(k L/2\right) = -\kappa D \exp\left(-\kappa L/2\right) ~.
\end{aligned}
\end{equation}
其中可以把 $E$ 看成未知量,决定 $\kappa, k$,$C,D$ 也是未知量。两式相除得
\begin{equation}
- \cot\left(k L/2\right) = \kappa /k~.
\end{equation}
这是一个超越方程,可能存在解。解出后再次代入
式 7 可以求得比值 $D/C$。归一化即可确定 $C, D$。现在我们尝试从图像上考察它可能的解。
利用 式 3 的关系,将 $\kappa$ 用 $k$ 表示,可以得到
\begin{equation}
- \cot\left(k L/2\right) =\sqrt{2mV_0/k^2-1}~.
\end{equation}
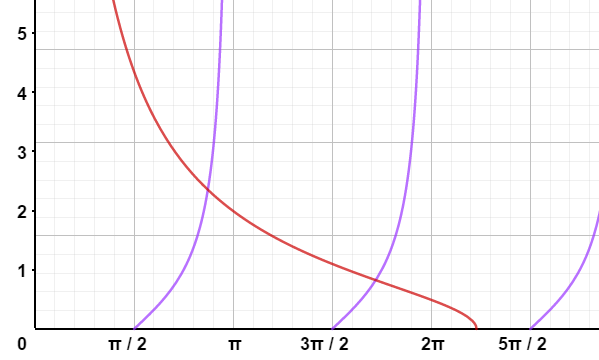
设 $z=k L/2$,我们可以在同一坐标系中绘制 $- \cot\left(z\right) $ 和 $\sqrt{(z_0/z)^2-1}$ 的图像($z_0=L\sqrt{2mV_0}/2$,表征了势阱 “大小”),两个图像的每一个交汇点都对应着一个奇函数解。图 2 显示了 $z_0=7$ 的情况,可以看到两个图像共有 $2$ 个交点。
图 2:方程 $-\cot z=\sqrt{(z_0/z)^2-1}$ 的解,$z_0=7$ 的情况(奇态)
对于宽深势阱($z_0=L\sqrt{2mV_0}/2$ 很大),两个图像一定有交。特别是当 $z_0\rightarrow\infty$ 时,交汇点的位置都可以近似为 $n\pi$($n$ 为正整数)。我们将在下面讨论偶波函数的时候具体分析这种情况。对于浅窄势阱,值得注意的是,当 $z_0<\pi/2$ 时无解,这可以从图像中看出。但此时仍有偶函数解,也就意味着至少存在一个束缚态。这将在后面进行讨论。
偶波函数
当波函数为奇函数时,易得 $\psi'(0) = 0$ 即 $C = 0$,且 $A = D$。与奇函数的情况同理得
\begin{equation}
\begin{aligned}
&B \cos\left(k L/2\right) = D \exp\left(-\kappa L/2\right) ~,\\
&k B \sin\left(k L/2\right) = \kappa D \exp\left(-\kappa L/2\right) ~.
\end{aligned}
\end{equation}
相除得
\begin{equation}
\tan\left(k L/2\right) = \kappa /k~.
\end{equation}
利用
式 3 的关系,将 $\kappa $ 用 $k$ 表示,可以得到
\begin{equation}
\tan\left(k L/2\right) =\sqrt{2mV_0/k^2-1}~.
\end{equation}
设 $z=k L/2$,我们可以在同一坐标系中绘制 $ \tan\left(z\right) $ 和 $\sqrt{(z_0/z)^2-1}$ 的图像($z_0=L\sqrt{2mV_0}/2$,表征了势阱 “大小”),两个图像的每一个交汇点都对应着一个偶函数解。
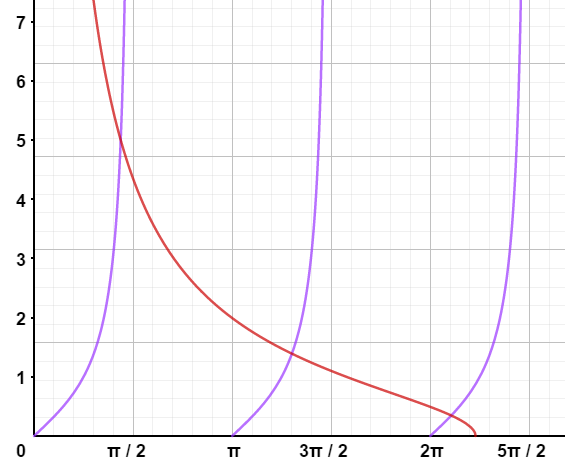
图 3 显示了 $z_0=7$ 的情况,可以看到两个图像共有 $3$ 个交点。
图 3:方程 $\tan z=\sqrt{(z_0/z)^2-1}$ 的解,$z_0=7$ 的情况(偶态)
现在来考虑两种情况:
1. 宽深势阱。即 $z_0=L\sqrt{2mV_0}/2$ 非常大。那么由图像可观察出,交汇点在略小于 $z_n=n\pi/2$($n$ 为奇数)的位置。所以有
\begin{equation}
E_n+V_0\approx \frac{\pi^2}{2mL^2}n^2\quad (n=1,3,5\cdots)~.
\end{equation}
当 $V_0\rightarrow \infty$ 时,有限深势阱转化为无限深势阱,上式右侧刚好是一维无限深势阱的能级(只包括了其中的一半,因为 $n$ 是奇数。另一半来自于奇函数)。当 $V_0$ 有限时,仅有有限多个束缚态。
2. 浅窄势阱。当 $z_0$ 降低时,束缚态越来越少,直到最后当 $z_0<\pi/2$ 时,仅存在一个束缚态。但无论势阱多么 “浅小”,总是至少存在一个束缚态,这可以由图像看出。
2. 散射态
散射态的计算只需要把 “方势垒” 中 $E > V_0$ 的情况下取 $V_0 < 0$ 即可,这里不再赘述。
1. ^ 参考 Wikipedia 相关页面 以及 [1]。
[1] ^ David Griffiths, Introduction to Quantum Mechanics, 4ed