贡献者: DTSIo; hfb25; addis
巴拿赫不动点定理(Banach fixed point theorem) 又称作压缩映像原理(contraction mapping principle). 它是完备度量空间理论中的基本定理,在分析数学的诸多分支中均有应用。
1. 两个著名例子
例 1 落在地面上的地图
这是数学科普中常见的命题:将一座公园的地图铺开在公园地面上,则地面上恰有唯一一点与地图上对应的点重合。
借助一点线性代数知识,这个命题是不难验证的。设公园可以用有界的面闭区域 $\bar\Omega$ 表示。设地图的压缩比是 $\lambda$ (它当然介于 0 和 1 之间). 现在固定一个平面直角坐标系,把地图铺在区域 $\bar\Omega$ 内,则从 $\bar\Omega$ 内的点(公园中的地点)到地图上对应点的变换由下面的公式给出:
$$
x\to \lambda Rx+b~,
$$
这里 $R$ 是一个旋转变换,$b$ 是平移向量。于是,要找的重合点必然满足方程
$$
x=\lambda Rx+b~.
$$
由于 $\|\lambda R\|=\lambda<1$, 这方程就有唯一的解
$$
x=(1-\lambda R)^{-1}b=\sum_{n=0}^{\infty}\lambda^nR^nb~.
$$
它就是要求的重合点。
例 2 函数的迭代
这是一个常见的数学实验:在计算器中任意输入一个数,而后不停地计算它的余弦值(弧度制), 会得到什么结果?
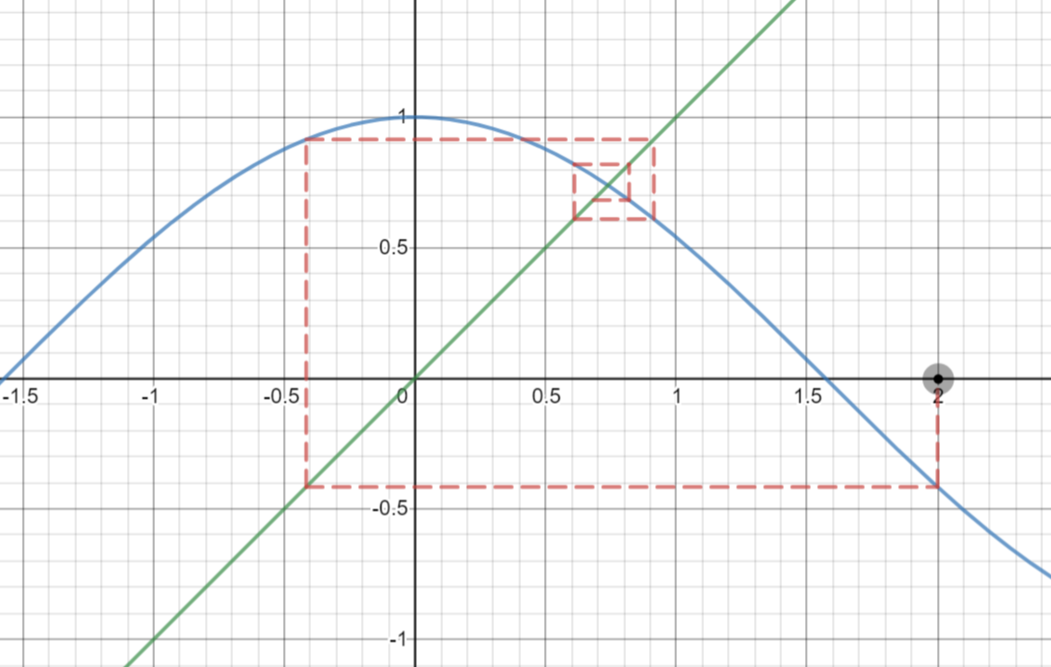
图 1:余弦函数的迭代
上图给出了一个结果; 迭代的结果越来越逼近对角线 $y=x$ 与余弦曲线 $y=\cos x$ 的唯一交点。验算若干数值,不难作出如下猜测:不论实数的迭代序列
$$
x_{n+1}=\cos x_n~
$$
开始于哪一个数,它最后都会收敛到方程 $x=\cos x$ 的唯一实数解 $x=0.739...$.
这个结论也可以严格证明。不论起点 $x_1$ 是何数,都有 $|x_2|=|\cos x_1|\leq 1$, 从而 $\cos 1\leq x_3\leq 1$. 这样一来,从 $x_3$ 开始,所有点都落在区间 $[\cos 1,1]$ 内。于是可以作出如下估计:
$$
\begin{aligned}
|x_{n+2}-x_{n+1}|
=\left|\int_{x_{n}}^{x_{n+1}}\sin tdt\right|
\leq (\sin 1)|x_{n+1}-x_n|.
\end{aligned}~
$$
由于 $|\sin1|<1$, 这表示序列 $\{x_n\}$ 是柯西序列,从而收敛到某个点 $x_*$. 对等式 $x_{n+1}=\cos x_n$ 取极限即看出这个极限点正是方程 $x=\cos x$ 的解。
2. 巴拿赫不动点定理
定理的表述
从上面所举的两个例子,可以抽象出如下的定理:
定理 1 巴拿赫不动点定理
设 $(X,d)$ 是完备度量空间, $T:X\to X$ 是其上的压缩映射,那么映射 $T$ 有唯一的不动点,即满足 $x=Tx$ 的点。而且,对于任意 $x_0\in X$, 点列 $\{T^nx_0\}_{n\in\mathbb{N}}$ 都收敛到这个不动点。
证明是直接的计算:根据度量空间中的三角不等式,显然有
$$
\begin{aligned}
d(T^nx_0,T^{n+k}x_0)
&\leq \sum_{j=1}^k d(T^{n+j-1}x_0,T^{n+j}x_0)\\
&\leq \sum_{j=1}^k q^{n+j-1}d(x_0,Tx_0)\\
&\leq \frac{q^n}{1-q}d(x_0,Tx_0).
\end{aligned}~
$$
于是点列 $\{T^nx_0\}_{n\in\mathbb{N}}$ 是柯西序列,在完备度量空间 $X$ 之中自然收敛到某个 $x_*\in X$. 在公式 $T^{n+1}x_0=T(T^nx_0)$ 中令 $n\to\infty$ 就立刻看出 $x_*=Tx_*$. 不动点的唯一性则由 $d(Tx,Ty)\leq qd(x,y)$ 立刻得到。证毕。
在上面的不等式中,如果令 $k\to\infty$, 就得到估计
$$
d(T^nx_0,x_*)\leq\frac{q^n}{1-q}d(x_0,Tx_0)~.
$$
这表示点列 $\{T^nx_0\}_{n\in\mathbb{N}}$ 收敛到不动点 $x_*$ 的速度很快,是指数式的。
辨析
从许多个意义上来说,巴拿赫不动点定理都是最优的,因为取消任何一条假设都能够让定理不成立(即存在反例).
例 3 没有完备性
这个例子非常简单。考虑开区间 $(0,1)$ 到自己的映射 $f(x)=x/2$. 它的不动点 $x=0$ 跑出了 $(0,1)$ 的范围。之所以会有这样的反例,是因为开区间 $(0,1)$ 在通常的距离函数之下并不是完备的度量空间。
例 4 没有一致的压缩比
巴拿赫不动点定理的表述要求一个无关于点 $x,y$ 的数 $q<1$, 这个数有时被称为压缩比。如果没有一致的压缩比,那么就能举出反例。例如函数
$$
f(x)=\frac{3}{4}x-\frac{1}{4}\sqrt{x^2+1},\,x\in\mathbb{R}~.
$$
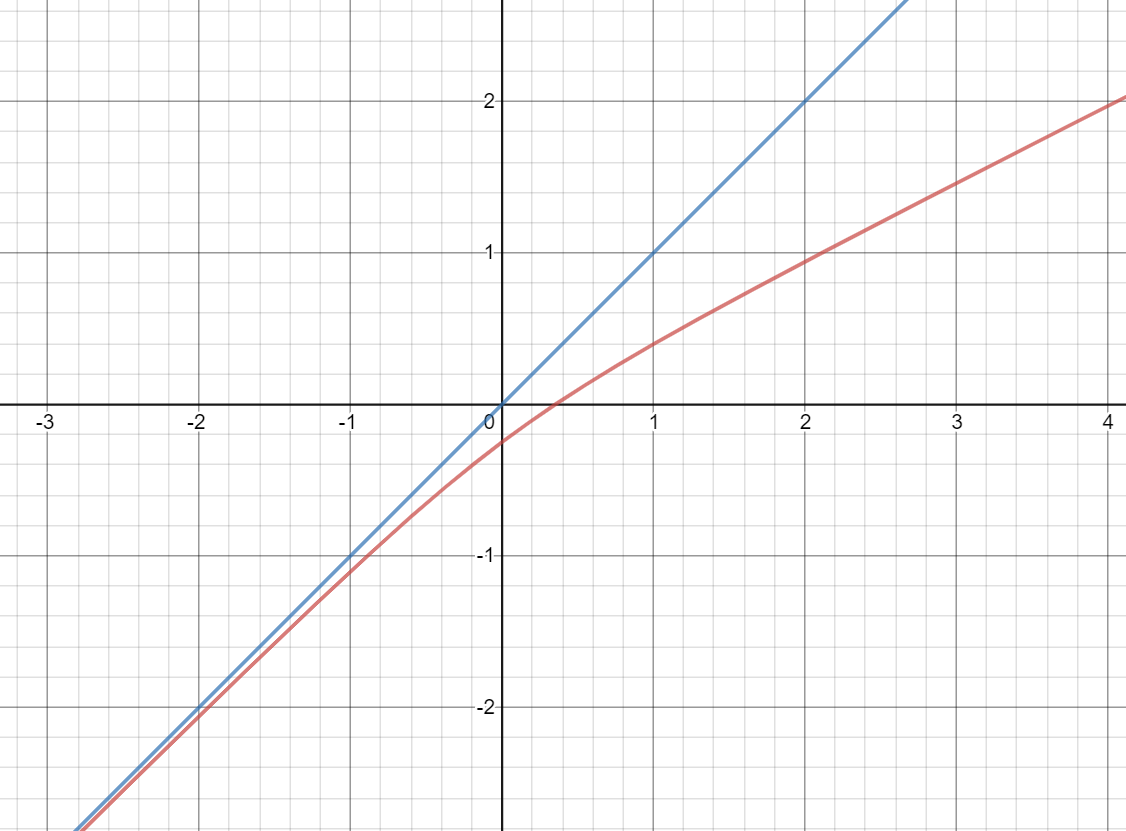
如图所示,它的图形是双曲线的一支,以对角线 $y=x$ 为渐近线。方程 $x=f(x)$ 当然无解。另一方面,通过微分中值定理,却也容易证明不等式
$$
|f(x_1)-f(x_2)|<|x_1-x_2|,\,x_1,x_2\in\mathbb{R}~.
$$
然而,当 $x_1,x_2\to-\infty$ 时,不难看出 $\frac{|f(x_1)-f(x_2)|}{|x_1-x_2|}$ 越来越接近 1. 因此映射 $f$ 没有一致的压缩比。
图 2:函数 $f(x)=\frac{3}{4}x-\frac{1}{4}\sqrt{x^2+1}$ 的图形
3. 应用举例
巴拿赫不动点定理在数学中有诸多应用。它可以用来证明方程存在唯一解,而且因为它的证明是构造性的,它还能够给出近似计算解的算法。
例 5 平方根的计算
对于给定的正数 $a$,它的算术平方根 $\sqrt{a}$ 一定满足方程 $x^2=a$。不妨设 $a>1$,将其改写为下列形式
\begin{equation}
\frac{1}{2} \left(x+\frac{a}{x} \right) =x~.
\end{equation}
将等式左边的部分视为 $Tx$,易知 $T$ 是完备度量空间
1 $[\eta,a]$($\eta$ 是一足够小正数
2)上的连续映射。
又对任意 $x_1,x_2\in [\eta,a]$
\begin{equation}
\left\lvert Tx_1 - Tx_2 \right\rvert =\frac{1}{2} \left\lvert x_1 - x_2 \right\rvert \left\lvert 1-\frac{a}{x_1x_2} \right\rvert \leq\frac{1}{2} \left\lvert x_1 - x_2 \right\rvert ~.
\end{equation}
根据巴拿赫不动点定理,我们可知算术平方根 $\sqrt{a}$ 必然存在且唯一,且对任意 $x\in[\eta,a]$,点列 $\{T^nx_0\}_{n\in\mathbb{N}}$ 均收敛到 $\sqrt{a}$.
所以我们可以这么计算正数 $a(a\geq 2)$ 的算术平方根:先取 $x_1=\frac{1}{2}a$3,然后按下式迭代计算:
\begin{equation}
x_{n+1}=\frac{1}{2} \left(x_n+\frac{a}{x_n} \right) ~.
\end{equation}
计算精度估计($n$ 为迭代计算次数)
\begin{equation}
\epsilon\leq \left(\frac{1}{2} \right) ^{n+1} \left\lvert a-4 \right\rvert ~.
\end{equation}
当 $1\leq a<2$ 时,取 $x_1=1$,此时计算精度估计
\begin{equation}
\epsilon\leq \left(\frac{1}{2} \right) ^{n-1} \left\lvert a \right\rvert ~.
\end{equation}
当 $0< a<1$ 时,求 $\sqrt{1/a}$,然后求倒数即可。
1. ^ 完备度量空间的闭子集必然是完备度量空间。
2. ^ $\eta$ 的值一方面要保证 $Tx\in[\eta,a](x\in[\eta,a])$,另一方面要保证 $x_1x_2 \geq a/2$ $(x_1,x_2\in[\eta,a])$,但可以证明 $\eta$ 是存在的(证明存在正数 $\eta$ 使 $a/2\leq \eta^2< a$)。
3. ^ 易证存在 $\eta\leq\frac{1}{2}a$ 且满足上面的条件。