有限对称群的性质

贡献者：叶月2_

预备知识　置换群、对称群，群的同态与同构

定义 1　

　　阶数为 1 或 2 的置换，称为对合变换（involution）。

定理 1　

　　任意有限置换群都可以表示为两个对合变换的复合。

　　 证明： 我们首先证明，循环置换可以分解为两个对合变换的复合。

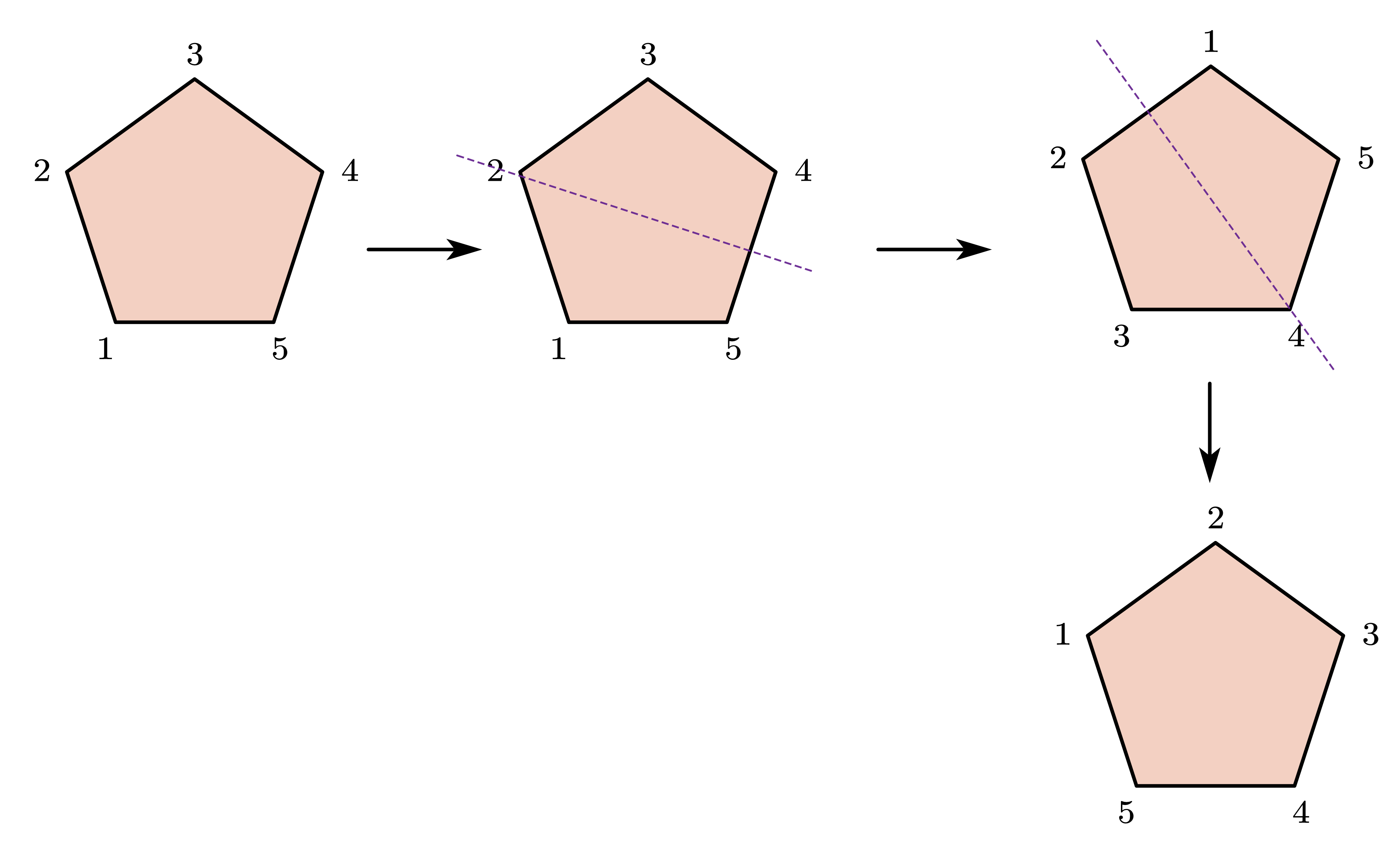
　　一个 n 元循环置换可以看作 n 边形上的旋转，而我们知道，二维空间上的旋转可以分解为两个反射，只要保证两次反射轴的夹角是旋转角度的 $1/2$，对合变换就是这种反射变换的置换表示。以正五边形为例，该过程如下所示：

图 1

　　该循环的分解写作 $(12345)=[(23)(14)][(13)(45)]$，显然，$[(13)(45)]$ 与 $[(23)(14)]$ 就是图中所示的 “反射变换”。

　　由于$n$ 元置换群总可以拆分成不相交的循环乘积，而每个循环都可以拆成对合之积，则这些对合可以重新组合成两组。如设某置换群可拆分成三个不相交循环之积，用 $\sigma$ 表示对合变换，且下标首字母不同代表不同循环，则有：

\begin{equation} \begin{aligned} f=f_1f_2f_3&=[\sigma_{11}\sigma_{12}][\sigma_{21}\sigma_{22}][\sigma_{31}\sigma_{32}]\\ &=[\sigma_{11}\sigma_{21}\sigma_{31}][\sigma_{12}\sigma_{22}\sigma_{32}]\\ &=\sigma'_1\sigma'_2~. \end{aligned} \end{equation}

得证。

　　从将循环元素的分解过程中，我们可以看到，对合变换是不相交的对换乘积，称这些不相交的对换为一个对合变换的组分。

有限置换群的自同构群

　　在本节，我们先阐明置换群的内自同构与群本身的关系，再阐明自同构与群的关系。

定理 2　

　　当 $n>2$ 时，$ \operatorname {Inn}S_n\cong S_n$

　　 证明：

　　由定理 3 得,$ \operatorname {Inn}S_n\cong S_n/C(S_n)$，因此我们只需要证明 $n>2$ 时，有限置换群的中心是单位元即可。

　　设任意 $\sigma_n\in C(S_n)-e$，那么 $\sigma_n$ 有三种可能，下面证明，每一种情况总能找到与之不交换的群元素。

若 $\sigma_n$ 是对换，比如 $(a\,b)$，则 $(b\,c)(a\,q)$ 必然与之不交换。
若 $\sigma_n$ 是 $k$ 循环，比如 $(a\,b\,c\,d)$，则 $(a\,b)$ 便与之不交换。
若 $\sigma_n$ 是不相交的循环乘积，则在两个循环里各取一元素，组成的对换与之不交换。

　　因此，$\sigma_n$ 是空集，$C(S_n)=e$，证明成立。

　　自同构是比内自同构更广些的概念，只要求双射同态。思及前文，我们已经证明任意置换都可以拆分成两个不相关的对合之复合。令对合变换表示为 $\sigma$，易证自同构将其映射为对合，因为 $f(\sigma^2)=f(e)=f^2(\sigma)$，且能把共轭类映射为共轭类，$f(\tau\sigma\tau^{-1})=f(\tau)f(\sigma)f^{-1}(\tau)$。下面我们来探讨，对合变换彼此共轭需要的条件。

引理 1　

　　对合变换共轭，当且仅当二者组分一致。

　　将对合变换 $\sigma$ 拆成一系列互不相交的组分乘积，然后用 $\tau$ 来做共轭变换，有几种可能结果：

$\tau$ 与 $\sigma$ 无相交元素，此时 $\tau\sigma\tau^{-1}=\sigma$，因此组分一致。
$\tau$ 与 $\sigma$ 其中一个组分只有一个相交元素，则 $\tau$ 的其他组分和 $\sigma$ 交换得 $e$，相交部分相乘后与 $\sigma$ 其他组分无相交，因此组分也一致¹。
$\tau$ 包含 $\sigma$ 的一个组分，则乘积结果为该组分，因此组分不变。
$\tau$ 的一个组分是在 $\sigma$ 的两个组分中各取一个元素。如 $(1\,4)[(1\,2)(3\,4)](1\,4)=(2\,4)(1\,3)$。
$\tau$ 是以上情况的任意组合，由于组分彼此互不相交，因此可交换位置到与 $\sigma$ 中的关联组分相邻，最后得到组分不变的结果。

　　这条引理告诉我们，可以利用组分数量来对对合变换进行共轭类划分。

　　因此我们可以设集合 $I_k^n$ 是 $S_n$ 中由 $k$ 个组分复合而成的的对合变换。考虑到一个组分是一个对换，$k\in[0,n/2]$。

　　因为自同构是同态映射，且把共轭类映射到共轭类，因此 $f(I_k^n)\subset I_{k'}^n,k'\in [0,n/2]$。又因为自同构是双射，所以若 $f(I_a^n)=f(I_b^n)$，则 $|I_a^n|=|I_b^n|$。所以为了聊自同构映射后的结果，我们需要研究对合集合的基数。

　　由对合集合的定义可知，$I_a^n$ 是从 $n$ 个元素中选取 $2a$ 个元素进行有序排列，且该排列里不同对换的顺序，以及一个对换里的元素顺序与对合变换的结果无关。因此，若设 $G_k=|I_k^n|$，则

\begin{equation} G_k=\frac{A_{n}^{2k}}{2^k\times k!}=\frac{n!}{2^k(n-k)!k!}~. \end{equation}

　　 若 $G_a=G_b$，唯一解得 $n=6$，此解为 $|I^6_3|=|I^6_1|$。解的唯一性说明除却 $n=6$，$f(I_k^n)=I_k^n$。

推论 1　

　　当 $n>2$ 且 $n\neq 6$ 时，$ \operatorname {Aut}S_n\cong S_n$。

　　该推论比定理 2 更强一些。由于 $ \operatorname {Inn}S_n\subset \operatorname {Aut} S_n$ 且 $ \operatorname {Inn}S_n\cong S_n$，因此我们只需要证明 $| \operatorname {Aut}S_n|=|S_n|$ 即可。

　　因为置换总可以拆成不相交的循环，因此我们先看自同构对循环的作用。由于循环是对合变换的乘积，而在 $n\neq 0$ 的时候，$f(I_k^n)=I_k^n$，因此自同构把对换映射为对换，且这种对换之间的映射是双射。比如对于任意 $f$，若设 $f(1\,2)=f(a\,b)=(c\,d)$，则

\begin{equation} f((1\,2)(a\,b))=f(1\,2)f(a\,b)=I~, \end{equation}

违反了自同构保元素阶数不变的性质。

　　对于 3 阶循环，我们有

\begin{equation} f(1\,2\,3)=f((1\,3)(1\,2))=f(1\,3)f(1\,2)=(a\,b)(c\,d)~, \end{equation}

因阶数之不变，$b=c,a\neq d$ 或 $b\neq c,a=d$。

　　同理可知，对于 $k$ 阶循环，自同构相当于将其映射到 $k$ 个对换上，可由 $k$ 个元素标记。现在取 $S_n$ 中的 $n$ 阶循环，令

\begin{equation} f(1\,2\,...n)=f(1\,n)f(1\,n-1)...f(1\,2)=(i_1\,i_n)(i_1\,i_{n-1})...(i_1\,i_2)~, \end{equation}

那么对于任意 $a,b\neq 1$ 必有 $f(a\,b)=(i_a\,i_b)$。因为 $f(a\,b)$ 与 $f(1\,a),f(1\,b)$ 都分别只包含一个相同元素。倘若包含的是 $i_1$，即 $f(a\,b)=(i_1\,i_k)$，则 $f(a\,b)=f(1\,k)$，违背 $f$ 的双射性。所以对于 $S_n$，任意 $f$ 实际上指定了一个双射 $a\rightarrow i_a$，$i_a$ 是从 1 至 $n$ 中指定一个元素，所以 $| \operatorname {Aut}S_n|=|S_n|$，得证。

1. ^ 譬如 $(2\,3)(3\,4)(2\,3)=(2\,4)$