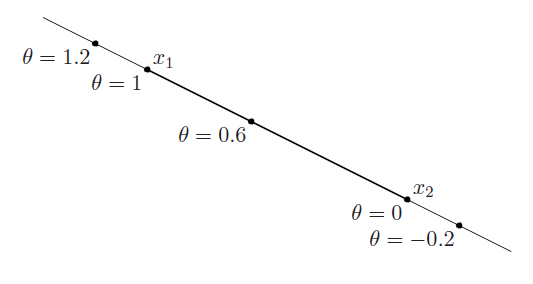贡献者: Giacomo; 零穹; xzllxls
仿射集是矢量空间中的一类子集,它起源于线性代数和几何学的共同发展。它是研究向量空间中点的集合性质的一种方式。在更广泛的背景下,其所对应的仿射几何已经成为几何学的一个重要分支。本文将介绍其基本概念和一些相关的定理。
定义 1 仿射组合与仿射集
取向量空间 $V$ (记其域为 $\mathbb{F}$) 中的两点 $x_1, x_2 \in V$ 的线性组合 $\theta x_1 + (1 - \theta) x_2$ 被称为 $x_1, x_2$ 的仿射组合;更一般的,系数和为一(即 $\sum_i a_i = 1$)的线性组合 $\sum_i a_i x_i$ 被称为 $x_1, \dots, x_n$ 的仿射组合。
向量空间的子集 $C \subseteq V$ 被称为仿射集(affine set),意味着 $C$ 中的任意仿射组合都在 $C$ 中;等价的,我们只需要考虑任意两个向量的仿射组合即可(和向量子空间的情况一样)。
图 1:仿射集示意图
图 $1$ 表示的是一条穿过 $x_1,x_2$ 两点的直线。当 $0 \leq \theta \leq 1$,形成图中直线加粗的部分;反之,形成直线上细线表示的部分。
从几何上看,仿射集仍然是平直的,或者说 “线性的”:
定理 1
对任意的仿射集 $C \subseteq V$,存在唯一的向量子空间 $U \subseteq V$,使得对任意的 $x \in C$,我们有
\begin{equation}
C = x + U = \{ x + v \mid v \in U\}~.
\end{equation}
证明:第一步,取一点 $x_0 \in C$,我们定义
\begin{equation}
U: = \{ x - x_0 \mid x \in C \}~,
\end{equation}
要证明它是一个向量子空间:
- $0_V = x_0 - x_0 \in U$,
- 对任意的 $a, b \in \mathbb{F}$,$x, y \in C$,
\begin{equation}
\begin{aligned}
a (x - x_0) + b (y - x_0) &= a x + b y - (a + b - 1) x_0 - x_0 \\
&= a x + b y + (1 - (a + b)) x_0 - x_0 \\
\end{aligned}~
\end{equation}
第二步,要证明对任意的 $x \in C$,$C = x + U$:首先证明 $\subseteq$,对任意的 $y \in C$,我们有
\begin{equation}
y = x + (y - x_0) - (x - x_0); ~
\end{equation}
现在证明 $\supseteq$,对任意的 $u = z - x_0 \in U$,我们有
\begin{equation}
x + u = x + z + (-1) x_0 ~
\end{equation}
是 $x, z, x_0$ 得仿射组合,证得。
第三步,要证明 $U$ 不依赖于 $x_0$ 的选取——对任意的 $x' \in C$,定义 $U': = \{x - x' \mid x \in C\}$,我们要证明 $U' = U$,处于对称性我们只需要证明 $U' \subseteq U$:取 $x \in C$,
\begin{equation}
x - x' = (x + x_0 - x') - x_0 ~
\end{equation}
$x + x_0 - x'$ 是 $x, x_0, x'$ 的仿射组合,因此证得。
第四步,证明 $U$ 的唯一性:假设 $V$ 存在另外一个向量子空间 $U'$ 满足对任意 $x \in C$,$C = x + U'$,取 $x = x_0$,那么 $x_0 + U' = x_0 + U \implies U' = U$。
证毕!
因此我们可以定义仿射集的维度
定义 2 维度
对于仿射集 $C \subseteq V$,我们定义它的维度为它对应的向量空间的维度。
特别的,一维的仿射集被称为仿射直线,二维的被称为仿射平面,余一维的被称为仿射超平面。
在向量空间中谈直线、平面、超平面时,我们有时指的是向量子空间,有时指的是仿射子空间,要注意分辨。
定理 2
对于向量空间的子集 $C \subseteq V$,$C$ 为仿射集当且仅当过 $C$ 中任意不同的两点的(仿射)直线仍然在 $C$ 中。
证明:必要性:假设 $C$ 是仿射集。那么任意由 $x_1,x_2\in C$ 确定的直线为 $x_1+(1-k)x_2,k\in\mathbb F$,即是 $x_1,x_2$ 的仿射组合,因此由仿射集的定义(定义 1 ),该直线属于 $C$。
充分性:设 $C$ 是过其上任意两点的直线都在 $C$ 中的集。那么任意 $x_i\in C,i=1,\cdots ,n$,对任意满足 $\sum_{i}a_i=1$ 的 $a_i\in\mathbb F$,成立(不失一般性,设 $a_1\neq1$)
\begin{equation}
\sum_{i=1}^n a_ix_i=(1-a_1)\sum_{i=2}^n \frac{a_i}{1-a_1}x_i+a_1x_1~.
\end{equation}
设 $n-1$ 时充分性成立。那么 $\sum_{i=2}^n \frac{a_i}{1-a_1}x_i\in C$,又
式 7 是 $\sum_{i=2}^n \frac{a_i}{1-a_1}x_i$ 和 $x_1$ 的仿射组合,因此 $\sum_{i=1}^n a_ix_i\in C$,即 对 $n$ 时充分性成立。根据数学归纳法和仿射集的定义,$C$ 是仿射集。
证毕!
推论 1
设 $U\subset V$ 是线性空间 $V$ 的子空间,$x\in V$,则 $x+U$ 是仿射集。
证明:任意 $x_1,x_2\in x+U$,设 $x_1=x+y_1,x_2=x+y_2$,其中 $y_1,y_2\in U$。则过 $x_1,x_2$ 的直线为
\begin{equation}
\{x_1+k(x_2-x_2)|k\in\mathbb F\}=\{x+(y_1+k(y_2-y_1))|k\in\mathbb F\}\subset x+U~.
\end{equation}
因为 $x_1,x_2$ 任意,所以由
定理 2 ,命题得证!
证毕!