约翰·冯·诺依曼
贡献者: 待更新
(本文根据 CC-BY-SA 协议转载自原搜狗科学百科对英文维基百科的翻译)
约翰·冯·诺伊曼(/vɒn ˈnɔɪmən/;匈牙利语:纽曼·雅诺斯·拉霍斯,发音;1903 年 12 月 28 日-1957 年 2 月 8 日)是匈牙利裔美国数学家、物理学家、计算机科学家和博学多才者。冯·诺伊曼被普遍认为是他那个时代最重要的数学家,[1] 并被称为 “伟大数学家的最后代表”;他是一个擅长融合纯科学和应用科学的天才。
他在许多领域做出了重大贡献,包括数学(数学基础、函数分析、遍历理论、表象理论、算子代数、几何、拓扑和数值分析)、物理(量子力学、流体力学和量子统计力学)、经济学(博弈论)、计算(冯·诺依曼架构、线性规划、自我复制机器、随机计算)和统计学。
他是将算子理论应用于量子力学发展函数分析的先驱,也是博弈论和细胞自动机概念、通用构造器和数字计算机发展的关键人物。
他一生发表了 150 多篇论文:大约 60 篇是纯数学论文,60 篇是应用数学论文,20 篇是物理论文,其余的是特殊数学或非数学学科的论文。[2]他的最后一部作品是他住院期间写的一份未完成的手稿,后来以书的形式出版了《计算机和大脑》。
他对自我复制结构的分析先于脱氧核糖核酸(DNA)结构的发现。在他提交给国家科学院(National Academy of Sciences)的一份罗列了他一生研究工作简短的清单表中,他说,“我认为最重要的研究工作是量子力学的研究,它是 1926 年在哥廷根发展起来的,随后又于 1927-1929 年在柏林发展。此外,我 1930 年在柏林大学和 1935-1939 年在普林斯顿大学期间,研究了各种形式的算子理论;1931-1932 年在普林斯顿大学,我研究了遍历定理。”
第二次世界大战期间,冯·诺伊曼与理论物理学家爱德华·泰勒(Edward Taller)、数学家斯塔尼斯瓦夫·乌兰(Stanislaw Ulam)等人一起参与曼哈顿计划,解决热核反应和氢弹中核物理的关键步骤问题。他创建了内爆型核武器中使用的爆炸透镜背后的数学模型,并创造了 “千吨”(梯恩梯 TNT)一词,作为所产生爆炸力的量度。
战后,他在美国原子能委员会总顾问委员会任职,并为许多组织提供咨询,包括美国空军、陆军弹道研究实验室、武装部队特种武器项目和劳伦斯·利弗莫尔国家实验室。作为一名匈牙利移民,他担心苏联会取得核优势,于是设计并推行了相互保证毁灭的政策,以限制军备竞赛。
1. 早期生活和教育
1.1 家庭背景
冯·诺伊曼原名为诺伊曼·雅诺斯·拉霍斯,他生于一个富裕的、适应新文化的、不循规蹈距的犹太家庭(在匈牙利,姓氏排在第一位)。他的名字在英语中等同于约翰·路易斯。
冯·诺伊曼出生在匈牙利王国布达佩斯,当时匈牙利是奥匈帝国的一部分。[3][4] 他是三个兄弟中的老大;他的两个弟弟妹妹是米哈伊尔(英文:迈克尔·冯·诺依曼;1907-1989)和米克尔斯(尼古拉斯·冯·诺伊曼,1911-2011)。[5]他的父亲诺依曼·米卡(马克斯·冯·诺依曼,1873-1928)是一名银行家,拥有法学博士学位。19 世纪 80 年代末,他从佩奇搬到布达佩斯。[6]米卡的父亲和祖父都出生在匈牙利北部泽姆普伦(Zemplen)县的翁德(Ond)(现在是泽伦茨(Szerencs)镇的一部分)。约翰的母亲是坎恩·玛姬特(英文:玛格丽特·坎恩)[7];她的父母是 Jakab Kann 和 Katalin Meisels。[8]坎恩家族的三代人都住在布达佩斯坎恩-赫勒办公室上方的宽敞公寓里;冯·诺依曼一家住在顶层的一套有 18 个房间的公寓里。[9]
1913 年 2 月 20 日,弗朗兹·约瑟夫皇帝将约翰的父亲提升为匈牙利贵族,以表彰他对奥匈帝国的贡献。诺伊曼家族因此获得了 “玛吉塔(Margitta)” 的世袭称谓,意思是 “玛吉塔”(今天罗马尼亚,玛吉塔)。这个家庭与这个城镇没有任何关系;这个称呼是根据玛格丽特选择的,正如他们选择的描绘三个玛格丽特的纹章一样。诺伊曼·诺伊曼·雅诺斯后来改名为诺玛姬塔·诺依曼·雅诺斯(约翰·诺伊曼·德·玛姬塔),后来改为德国约翰·冯·诺伊曼。
1.2 神童
冯·诺依曼是个神童。当他 6 岁的时候,他能在脑子里进行两个 8 位数的除法[10][11],还能用古希腊语交谈。当 6 岁的冯·诺依曼发现母亲漫无目的地盯着他时,他问她,“你在盘算什么?”[12]
匈牙利的儿童直到 10 岁才开始正式上学;家庭女教师教导冯·诺依曼、他的兄弟和堂兄弟姐妹。马克斯认为除了匈牙利语之外,语言知识也很重要,所以孩子们接受了英语、法语、德语和意大利语的辅导[13]。到 8 岁时,冯·诺伊曼对微积分就很熟悉了,但他对历史特别感兴趣。他阅读了威廉·昂肯(Wimhelm Oncken)的 46 卷本《Allgemeine Geschichte in Einzeldarslellungen》。马克斯购买的一个私人图书馆里有一份副本。公寓里的一个房间被改造成了图书馆和阅览室,书架从天花板延伸到了地板。[14]
冯·诺伊曼于 1911 年加入路德教(Lutheran Fasori Evangélikus Gimnázium)。尤金·维格纳比冯·诺依曼早一年进入路德教会学校,并很快成为了他的朋友[15]。这是布达佩斯最好的学校之一,也是为精英设计的优秀教育体系的一部分。在匈牙利体制下,孩子们在一所体育馆接受所有教育。匈牙利的学校体系造就了以智力成就著称的一代人,其中包括西奥多·冯·卡尔曼(1881 年)、乔治·德·赫维希(1885 年)、迈克尔·波兰尼(1891 年)、莱昂斯·西拉德(1898 年)、丹尼斯·加博尔(1900 年)、维格纳(1902 年)、爱德华·泰勒(1908 年)和保罗·erdős(1913 年)。[16]这批人有时被称为 “火星人”。[17]
虽然马克斯坚持冯·诺依曼在适合他年龄的年级上学,但他同意聘请私人教师,在他表现出天赋的领域给他高级指导。15 岁时,他开始在著名分析师 Gábor·szegő.的指导下学习高级微积分[15],他们第一次见面时,Szegő被这个男孩的数学天赋惊呆了,他激动地留下了眼泪。冯·诺依曼对 Szegő在微积分中提出的问题的一些即时解决方案被描绘在他父亲的信纸上,现在仍在布达佩斯的冯·诺依曼档案馆展出[15]。到 19 岁时,冯·诺伊曼已经发表了两篇重要的数学论文,其中第二篇给出了序数的现代定义[18],取代了乔治·康托的定义。在体育馆结束学业后,冯·诺伊曼参加并获得了国家数学奖——厄茨奖。[19]
1.3 大学学习
根据他的朋友西奥多·冯·卡门的说法,冯·诺依曼的父亲希望约翰跟随他进入工业界,从而把他的时间投入到比数学更有经济价值的工作中。事实上,他的父亲要求西奥多·冯·卡门说服他的儿子不要把数学作为他的专业。[20]冯·诺依曼和他的父亲决定最好的职业道路是成为一名化学工程师。冯·诺伊曼对此知之甚少,所以他被安排在柏林大学学习两年的非学位化学课程,之后他参加了著名苏黎世联邦理工学院(ETH Zurich)的入学考试[21],并于 1923 年 9 月通过了[22]。与此同时,冯·诺伊曼(von Neumann)也进入布达佩斯的帕兹曼·彼得大学,作为数学博士候选人。在论文中,他选择的主题为康托集合论的公理化。[23][24] 他于 1926 年从苏黎世联邦理工学院毕业,成为一名化学工程师(尽管魏格纳说冯·诺依曼从来就不太喜欢化学这门学科)[25],并在获得化学工程学位的同时通过了数学博士学位的最后的考试,其中魏格纳写道,“显然,博士论文和考试并没有给他带来太大的压力。”[25]然后,他在洛克菲勒基金会的资助下进入了哥廷根大学,在戴维·希尔伯特的指导下学习数学。[26]
2. 早期职业和私人生活
冯·诺伊曼在 1927 年 12 月 13 日完成了他的教授论文,并于 1928 年作为一名编外讲师在柏林大学开始了他的授课,[27]成为该大学历史上任何学科中最年轻的一位授课教师。[28]到 1927 年底,冯·诺伊曼已经发表了 12 篇数学专业学术论文,到 1929 年底,以每月近一篇专业学术论文的速度发表了 32 篇论文。[29]他具有很强的记忆和回忆的能力,这使他能够快速记忆电话簿的页面,并背诵其中的姓名、地址和号码。[30]1929 年,他短暂地成为汉堡大学的私人教师,那里成为终身教授的前景更好[30],但同年 10 月,当他被邀请到新泽西州普林斯顿的普林斯顿大学时,一个更好的机会出现了。[31]
1930 年的元旦,冯·诺伊曼娶了玛丽埃塔·柯维斯(Marietta Kovesi),她曾在布达佩斯大学学习经济学。[31]冯·诺依曼和玛丽埃塔有一个孩子,女儿玛丽娜,出生于 1935 年,截至 2017 年,她是密歇根大学工商管理和公共政策的杰出教授。[32]这对夫妇于 1937 年离婚。1938 年 10 月,冯·诺伊曼与克拉拉·丹结婚,克拉拉·丹是他在二战爆发前最后一次回布达佩斯时遇到的。[33]
冯·诺依曼在与玛丽埃塔结婚之前,于 1930 年受洗成为天主教徒。[34]冯·诺依曼的父亲马克斯于 1929 年去世。马克斯在世时,家里没有一个人皈依基督教,但后来都皈依了。[35]
1933 年,当新泽西高等研究院任命赫尔曼·韦勒为终身教授的计划落空时,他被授予终身教授职位。[36]他在那里一直担任数学教授,直到去世,尽管他已经宣布打算辞职,成为加州大学的一名讲座教授。[37]1939 年,他的母亲、兄弟和姻亲跟随冯·诺依曼来到美国。[38]冯·诺依曼把他的名字英语化为约翰,保留了冯·诺依曼的德国贵族姓氏。他的兄弟们把他们的名字换成了 “诺依曼” 和 “冯尼曼”。[39]冯·诺伊曼(Von Neumann)于 1937 年加入美国国籍,并立即试图成为美国陆军军官后备队的中尉。他轻而易举地通过了考试,但最终由于年龄原因被拒绝了。[39]他战前对法国如何对抗德国的分析经常被引用:“哦,法国不重要。”[40]
克拉拉和约翰·冯·诺依曼在当地学术界非常活跃。[41]他在韦斯特科特路 26 号的白色隔板房子是普林斯顿最大的私人住宅之一。[42]他非常注重自己的衣服,总是穿正式的西装。有一次,他骑着骡子穿过大峡谷时,身上穿了一套三件套的细条纹套装。[43]据说希尔伯特在冯·诺伊曼 1926 年的博士考试中曾问:“请问,这位候选人的裁缝是谁?”,因为他从未见过如此漂亮的晚礼服。[44]
冯·诺依曼一生热爱古代史,以其惊人的历史知识而闻名。普林斯顿的拜占庭历史教授曾说冯·诺伊曼在拜占庭历史方面比他更专业。[45]
冯·诺伊曼喜欢吃喝;他的妻子克拉拉说,除了卡路里,他什么都能计数。他喜欢意第绪语和 “低俗的” 幽默(尤其是打油诗)。[46]他不吸烟。[46]在普林斯顿,他因经常在留声机上播放极其响亮的德国进行曲而受到投诉,这些音乐让包括阿尔伯特·爱因斯坦在内的在邻近办公室工作的邻居们都无法专心工作。[47]冯·诺伊曼在嘈杂、混乱的环境中完成了一些最出色的工作,他曾经告诫他的妻子为他准备一间安静的书房,但他从来没有用过它,更喜欢在他们夫妇的客厅里大声放着电视。[48]尽管他是一个出了名的坏司机,但他仍然喜欢开车——经常是一边看书一边开车——这导致了多次被逮捕和多起交通事故。当库斯伯特·赫德雇用他为 IBM 公司的顾问时,赫德经常悄悄地为他的交通罚单支付罚款。[49]
冯·诺伊曼在美国最亲密的朋友是数学家斯塔尼斯瓦乌拉姆(Stanistlaw Ulam)。乌兰后来的一个朋友吉安-卡尔洛·罗塔写道,“他们会花几个小时没完没了地闲聊和咯咯笑,交换犹太笑话,并时不时地聊到数学话题。” 当冯·诺依曼在医院里奄奄一息时,每次乌拉姆来访,他都会带着一套新的笑话来逗他开心。[50]他相信他的许多数学思想都是凭直觉产生的,他经常会带着一个未解决的问题睡觉,一醒来就能知道答案。[48]乌兰指出,冯·诺依曼的思维方式可能不是视觉的,而是听觉的。[51]
3. 数学
3.1 集合论
在欧几里德(Euclid)的元素模型基础上,数学的公理化在 19 世纪末达到了新的严谨和广度水平,特别是在算术上,要归功于理查德·戴德金和查尔斯·桑德斯·皮尔士的公理化模式,在几何学上,这要归功于希尔伯特的公理化。[52]但是在 20 世纪初,将数学建立在朴素集合论基础上的努力由于罗素悖论(建立在不属于自己的所有集合的集合上)而受挫。[53]大约二十年后,恩斯特·策梅洛(Ernst Zermelo)和亚伯拉罕·弗兰肯(Abraham Fraenkel)暗中解决了集合论充分公理化的问题。zermelo–Fraenkel 集合论提供了一系列原则,允许构建日常数学实践中使用的集合,但它们没有明确排除存在属于自身的集合的可能性。冯·诺依曼在 1925 年的博士论文中展示了排除这种集合的两种技术——基础公理和阶级概念。[52]
根据基础公理,每一个集合都可以通过策梅洛和弗兰肯的原则,从下到上,按照一系列有序的步骤来构造。如果一个集合属于另一个集合,那么第一个集合必须在连续的第二个集合之前。这排除了一个集合属于它自己的可能性。为了证明把这个新公理加到其他公理上并没有产生矛盾,冯·诺依曼引入了一种证明方法,称为内模法,后来它成为集合论中的一种基本工具。[52]
第二种解决属于自己的集合问题的方法以类的概念为基础,将集合定义为属于其他类的类,而适当的类定义为不属于其他类的类。在策梅洛-弗兰科尔(Zermelo-Fraenkel)方法下,公理阻碍了不属于自己的所有集合的构造。相反,在冯·诺依曼方法下,所有不属于自己的集合的类都可以被构造,但它是一个适当的类而不是集合。[52]
由于冯·诺依曼的这一贡献,集合理论的公理系统避免了早期系统的矛盾,并成为可用的数学基础,尽管缺乏其一致性的证明。下一个问题是,它是否能为所有可能在其中提出的数学问题提供明确的答案,或者是否可以通过添加更强有力的公理来改进它,这些公理可以用来证明更广泛的一类定理。后来,这个问题得到了强有力的否定回答,1930 年 9 月,在历史悠久的柯尼希斯堡数学大会上,库尔特·哥德尔宣布了他的第一个不完全性定理:通常的公理系统是不完整的,就这个意义而言,它们不能证明用他们的语言表达的每一个真理。此外,这些系统的每一次持续扩展都必然是不完整的。[54]
过了不到一个月,参加大会的冯·诺依曼向哥德尔传达了他的定理的一个有趣的结果:通常的公理系统无法证明它们自己的一致性。[54]然而,哥德尔已经发现了这个结果,现在被称为他的第二个不完全性定理,他给冯·诺依曼寄去了一份他的文章的预印本,其中包含两个不完全性定理。[55]冯·诺伊曼在下一封信中承认哥德尔的优先地位。[56]他从来没有过多考虑 “美国人事事以个人利益为重的制度”。[57]
冯·诺依曼悖论
在费利克斯·豪斯多夫工作的基础上,斯特凡·巴拿赫和阿尔弗雷德·塔尔斯基在 1924 年证明了在三维空间中给定一个实心球,球会分解成有限数量的不相交子集,这些子集可以用不同的方式重新组合在一起,产生原始球的两个完全相同的副本。巴纳赫和塔尔斯基证明,使用等距变换,将一个二维图形的拆开并重新组合,其面积必然与原始图形相同。这样就不可能把一个正方形变成两个正方形。然而,在 1929 年的一篇论文中,[58]冯·诺依曼证明了反常分解可以使用一组转换,其中包括一个带有两个生成器的自由群作为子群。面积保持变换的组包含这些子组,这提供了使用这些子组进行反常分解的可能性。冯·诺依曼在他关于巴拿赫-塔尔斯基分解的工作中分离出的一类群随后对数学的许多领域都非常重要,包括冯·诺依曼自己后来在测量理论方面的工作(见下文)。
3.2 遍历理论
在 1932 年发表的一系列著名论文中,冯·诺伊曼对遍历理论作出了基础性贡献。遍历理论是数学的一个分支,涉及具有不变测度的动力系统的状态。[59]在 1932 年关于遍历理论的论文中,保罗·哈尔莫斯写道,即使 “冯·诺依曼从未做过任何其他事情,这也足以保证他在数学上不朽的声名”。[60]那时冯·诺依曼已经写了他著名的算子理论文章,这项工作的应用在冯·诺依曼平均遍历定理中起了重要作用。[60]
3.3 算子理论
冯·诺依曼通过冯·诺依曼代数引入了算子环的研究。冯诺依曼代数是希尔伯特空间上有界算子的*-代数,它在弱算子拓扑中是封闭的,并且包含恒等式算子。[61]冯·诺伊曼双突变定理表明,解析定义等同于纯代数定义,等于双突变体。[62]冯·诺依曼在 1936 年开始着手于冯·诺依曼代数的因子分类的一般性研究,并得到了默里的部分合作。1936 年至 1940 年间,他在六篇重要论文中提出了这一理论,这六篇论文 “跻身于二十世纪的分析杰作之列”。[63]约翰·冯·诺依曼后来在 1949 年引入了直接积分。[63]
3.4 测度论
在测度理论中,n 维欧氏空间 Rn 的 “测度问题” 可以表述为:“Rn 的所有子集的类上是否存在一个正的、归一化的、不变的和可加的集合函数?”[60]费利克斯·豪斯多夫和斯特凡·巴拿赫的工作己经暗示,在所有其他情况下,如果 $n = 1$ 或 $n = 2$,测度问题有一个正解,和一个负解(因为巴拿赫-塔尔斯基悖论)。冯·诺依曼的工作认为 “问题本质上是群论性质的”:[60]一个测度的存在可以通过观察给定空间的变换群的性质来确定。至多两维空间的正解和更高维空间的负解来自于欧几里德群是至多两维空间的可解群这一事实,并且对于更高维空间是不可解的。“因此,根据冯·诺伊曼的观点,造成差异的是群体的变化,而不是空间的变化。”[60]
在冯·诺依曼的许多论文中,他使用的论证方法被认为比结果更有意义。冯·诺依曼在他以后对算子代数中维数理论的研究中,利用有限分解的等价结果,用函数重新表述了测度问题。[64]在他 1936 年关于分析测度理论的论文中,他在紧群情况下用哈尔定理求解希尔伯特第五问题。[60][65] 1938 年,他因在分析方面的杰出研究而被授予伯歇纪念奖。[66]
3.5 几何学
冯·诺依曼创立了连续几何领域。[67]他继承了他对算子环的开创性工作。在数学中,连续几何是复杂射影几何的替代,其中子空间的维数不是离散集 0,1,...,n,它可以是单位区间[0,1]的一个元素。在此之前,门格尔和伯克霍夫已经根据线性子空间格的性质将复射影几何公理化。冯·诺依曼在继续算子环方面的研究时,弱化了这些公理来描述更广泛的格类——连续几何。虽然射影几何子空间的维数是一个离散集(非负整数),但连续几何元素的维数可以在单位区间内连续变化。冯·诺依曼的研究动机是他发现了冯·诺依曼代数,其维数函数取连续的维数范围,而第一个不同于射影空间的连续几何的例子是超有限第二类因子的投影。[68][69]
3.6 晶格理论
在 1937 年到 1939 年间,冯·诺依曼致力于晶格理论的研究,这是一种半序集理论,其中每两个元素有一个最大的下界和一个最小的上界。加勒特·伯克霍夫写道:“约翰·冯·诺依曼的聪明才智像流星一样闪耀在晶格理论之上”。[70]
冯·诺伊曼(Von Neumann)对完备的补模拓扑格(内积空间子空间格中出现的性质)中的维数进行了抽象探索:“维数由以下两个性质决定,直到正线性变换。它由透视映射(“透视”)保存,并由包含物排序。证据的最深层部分涉及透视性与 “分解投射性” 的等价性——其推论是透视性的传递性。[70]
另外,“在一般情况下,冯·诺依曼证明了以下基本表示定理。任何具有 n ≥ 4 个成对透视元素 “基” 的补模格 L,都与一个合适正则环 r 的所有主右理想的格ℛ(R)同构。这个结论是 140 页包含全新公理的精彩精辟代数的顶峰。任何想对冯·诺依曼头脑中的惊心动魄的才华留下难忘印象的人,只需努力为自己追寻这一系列精确的推理埸景——想象那个天才常常穿着浴袍坐在客厅里的写字台旁,随手写下五页充满智慧的想法。”[70]
3.7 量子力学的数学公式
冯·诺依曼在 1932 年的著作《量子力学的数学基础》中首次为量子力学建立了严格的数学框架,即狄拉克-冯·诺依曼公理。[64]在完成集合论的公理化之后,他开始面对量子力学的公理化。他在 1926 年意识到,量子系统的状态可以用(复杂的)希尔伯特空间中的一个点来表示,一般来说,即使是单个粒子,这个点也可以是无限维的。在量子力学的这种形式中,位置或动量等可观测的量被表示为作用于与量子系统相关的希尔伯特空间的线性算子。[71]
量子力学的物理学因此被简化为希尔伯特空间和作用于其上的线性算子的数学。例如,根据不确定性原理,粒子位置的确定阻止了动量的确定(反之亦然),被转化为两个相应算子的不可交换性。这个新的数学公式作为特例包括海森堡和薛定谔的公式。[71]当海森堡被告知冯·诺依曼已经阐明了作为自伴算子的无界算子和仅仅是对称算子之间的区别时,海森堡回答道:“嗯?有什么区别?”[72]
冯·诺依曼的抽象处理也使他能够面对决定论和非决定论的基本问题,他在书中提出了一个证据,证明量子力学的统计结果不可能像经典统计力学那样是一组确定的 “隐藏变量” 的平均值。1935 年,格雷特·赫尔曼(Grete Hermann)发表了一篇论文,认为该证明包含一个概念性错误,因此无效。[73]赫尔曼的工作在基本上被忽视了,直到约翰·贝尔在 1966 年提出了本质上相同的论点。[74]然而,在 2010 年,杰弗里·布博(Jeffrey Bub)认为贝尔误解了冯·诺依曼的证明,并指出该证明虽然并不适用于所有的隐藏变量理论,但确实排除了一个定义明确且重要的子集。布博还指出冯·诺依曼意识到了这一局限性,冯·诺依曼并没有声称他的证明完全排除了隐藏变量理论。[75]反过来,Bub 的论点的有效性也有争议。[76]无论如何,格里森 1957 年的理论填补了冯·诺依曼方法的空白。
冯·诺依曼的证明开创了一条研究路线,最终通过贝尔在 1964 年研究的贝尔定理,以及阿兰 Aspect 在 1982 年的实验,证明量子物理要么需要一个与经典物理学完全不同的现实概念,要么必须包含明显违反狭义相对论的非局域性。[77]
在《量子力学的数学基础》一章中,冯·诺依曼深入分析了所谓的测量问题。他得出结论,整个物理宇宙可以服从宇宙波函数。由于需要 “计算之外” 的东西来瓦解波函数,冯·诺依曼得出结论,瓦解是由实验者的意识引起的。冯·诺依曼认为量子力学的数学允许波函数的崩溃被放置在从测量装置到人类观察者的 “主观意识” 的因果链中的任何位置。尽管这一观点被尤金·维格纳(Eugene Wigner)所接受[78],但冯·诺伊曼-魏格纳的解释从未得到大多数物理学家的认可。[79]冯·诺伊曼-魏格纳的解释概述如下:
量子力学的规则是正确的,但是只有一个系统可以用量子力学来处理,那就是整个物质世界。存在着量子力学无法处理的外部观察者,即人类(或许还有动物)的大脑,他们对大脑进行测量,导致波函数崩溃。
尽管量子力学的理论一直发展到今天,但量子力学存在一个数学形式主义难题的基本框架,它是大多数方法的基础,可以追溯到冯·诺伊曼最先使用的数学形式主义和技术。换句话说,关于理论解释及其扩展的讨论,现在大多是在对数学基础的共同假设的基础上进行的。[64]
冯·诺依曼熵
冯诺依曼熵在量子信息论框架中以不同的形式(条件熵、相对熵等)得到了广泛的应用。其纠缠度测量是基于与冯·诺依曼熵直接相关的一些量。给定具有密度矩阵的量子力学系统的统计系综 $\rho$,它来源于 $S(p)=-Tr(\rho ln\rho)$ 经典信息论中许多相同的熵测度也可以推广到量子情况,如霍尔沃熵和条件量子熵。
量子互信息
量子信息论很大程度上与冯·诺依曼熵的解释和应用有关。冯·诺依曼熵是量子信息论发展的基石,而香农熵则适用于经典信息论。鉴于冯·诺依曼熵在量子信息论中的更广泛应用,这被认为是一个历史异常,因为可以预计香农熵是早于冯·诺依曼熵之前发现的。然而,历史发生了逆转。冯·诺依曼首先发现了冯·诺依曼熵,并将其应用于统计物理问题。几十年后,香农提出了一个用于经典信息论的信息论公式,并问冯·诺伊曼如何称呼它,冯·诺伊曼告诉他称之为香农熵,因为这是冯·诺伊曼熵的一个特例。[80]
密度矩阵
密度算子和矩阵的形式体系是冯·诺伊曼[81]在 1927 年独立提出的,但勒夫·兰道[82]和费利克斯·布洛赫[83]也分别在 1927 年和 1946 年没有那么系统地提出来。密度矩阵是表示量子系统状态的另一种方法,否则可以用波函数来表示。密度矩阵可以解决量子力学中某些与时间相关的问题。
冯·诺依曼测量方案
冯·诺依曼测量方案是量子退相干理论的鼻祖,它通过考虑也被视为量子对象的测量仪器来以投影地方式表示测量结果。冯·诺依曼提出的 “投影测量” 方案推动了量子退相干理论的发展。[84]
3.8 量子逻辑
冯·诺依曼在 1932 年的论文《量子力学的数学基础》中首次提出了量子逻辑,他指出希尔伯特空间上的投影可以被看作是关于物理可观测性的命题。量子逻辑领域随后由冯·诺依曼和加勒特·伯克霍夫(Garrett Birkhoff)在 1936 年的一篇著名论文中开创出来,这是有始以来第一部引入量子逻辑的著作[85],其中冯·诺依曼和伯克霍夫首次证明了量子力学需要一种与所有经典逻辑本质不同的命题演算,并严格隔离了量子逻辑的新代数结构。在冯·诺依曼 1932 年的著作中,为量子逻辑创建命题演算的概念首先在一个简短的章节中被概述,但是在 1936 年,新命题演算的需要通过几个论证得到证明。例如,光子不能通过两个垂直偏振的连续滤光器(例如,一个水平偏振,另一个垂直偏振),因此,更不必说,如果对角偏振的第三滤光器被添加到另外两个滤光器中,或者在它们连续之前或者之后,光子也不能通过,但是如果第三滤光器被添加到另外两个滤光器之间,光子将确实能够通过。这个实验事实可以转化为逻辑,因为连接是不可交换的 $(A\land B)\ne(B\land A)$。也证明了经典逻辑的分布规律,$P\lor (Q\land R)=(P \lor Q)\land(P \lor R)$ 和 $P\land (Q\lor R)=(P \land Q)\lor (P \land R)$,对量子理论无效。[86]
其原因是量子分离不同于经典分离,即使两个分离都是假的,量子分离也可能是真的,这反过来又归因于这样一个常常出现的事实,在量子力学中,一对选择在语义上是确定的,而其每个成员必然是不确定的。后一个特性可以通过一个简单的例子来说明。假设我们处理的是半积分自旋(自旋角动量)的粒子(如电子),它们只有两个可能的值:正的或负的。然后,一个不确定性原理确定相对于两个不同方向(例如,$x$ 和 $y$)的自旋导致一对不相容的量。假设某个电子的状态 $\Phi$ 证明了 “电子在 x 方向的自旋是正的” 这一命题,根据不确定性原理,$\Phi$.在 $y$ 方向上的自旋值是完全不确定的,因此,$\Phi$ 既不能证明 “$y$ 方向的自旋是正的” 命题,也不能证明 “$y$ 方向的自旋是负的” 命题,然而,“$y$ 方向的自旋是正的,或者 $y$ 方向的自旋是负的” 命题的分离对 $\Phi$.来说肯定是正确的。因此,在分配的情况下,有可能出现以下情况 $A\land (B \lor C)=A \land 1=A$,而 $(A \land B)\lor (A \land C)=0 \lor 0=0$
正如希拉里·普特南所述,冯·诺依曼用构造在正交模格(同构于给定物理系统希尔伯特空间的子空间格)中的逻辑取代了经典逻辑。[87]
3.9 博弈论
冯·诺依曼创立了博弈论领域作为一门数学学科。[88]冯·诺依曼在 1928 年证明了他的极大极小定理。这个定理证明,在具有完美信息的零和博弈中(即玩家每次都知道到目前为止已经发生的所有移动),两个玩家都有一对策略,允许每个人都可能将他的最大损失最小化,因此被称为极大极小。在研究每一个可能的策略时,玩家必须考虑对手所有可能的反应。然后,玩家会制定出将最大损失最小化的策略。[89]
这种使每个玩家的最大损失最小化的策略被称为最优策略。冯·诺伊曼证明了它们的极小极大值是相等的(绝对值)和相反的(符号)。冯·诺伊曼改进并扩展了极大极小定理,将包含不完全信息的博弈和拥有两个以上玩家的博弈纳入其中,并在他 1944 年的《博弈与经济行为理论》(与奥斯卡·莫根施特恩合著)中公布了这一结果。莫根斯特恩(Oskar Morgenstern)写了一篇关于博弈论的论文,想到冯·诺依曼对这个课题很感兴趣,就写信寄给了他。冯·诺伊曼读了信,对莫根斯特恩回信说,他应该再多写一些。这样来回重复了几次,然后冯·诺依曼变成了合著者,论文长达 100 页。再后来它变成了一本书。公众对这项研究进展的兴趣如此之大,以至于《纽约时报》刊登了一篇头版报道。在这本书里,冯·诺依曼(von Neumann)宣称,经济理论需要使用泛函分析方法,特别是凸集和拓扑不动点定理,而不是传统的微分,因为最大算子并不保留可微函数。[88]
列昂尼德·坎特罗维奇(Leonid Kantorovich)独自在数学经济学上的函数分析的研究中,也把注意力集中在了最优化理论、不可微性和向量格上。冯·诺依曼的泛函分析技术——使用实向量空间的对偶对来表示价格和数量,使用支持和分离超平面和凸集,以及不动点理论——从此成为数学经济学的主要工具。[90]
3.10 数学经济学
冯·诺伊曼在一些有影响力的出版物中提高了经济学的知识和数学水平。冯·诺依曼用他对布劳威尔不动点定理的推广证明了他的经济扩张模型中均衡的存在性和唯一性。[88]冯·诺依曼的扩张经济模型考虑了矩阵束 A-λB 与非负矩阵 A 和 B;冯·诺伊曼寻找概率向量 p 和 q 以及一个正数λ来求解互补方程 $$P^T=(A-\lambda B)q=0~$$ 以及表达经济效率的两个不平等系统。在这个模型中,(换位的)概率向量 $p$ 代表商品的价格,而概率向量 $q$ 代表生产过程运行的 “强度”。唯一解 $\lambda$ 代表 1 加上经济增长率的增长因子;增长率等于利率。[91][92]
冯·诺依曼的结果被视为线性规划的特例,其中冯·诺依曼的模型仅使用非负矩阵。冯·诺依曼的经济扩张模型的研究继续引起对计算经济学感兴趣的数学经济学家的兴趣。[93][94][95] 这篇论文被几个作者称为数学经济学中最伟大的论文,他们认识到它引入了不动点定理、线性不等式、互补松弛和鞍点对偶。在冯·诺依曼增长模型会议记录中,保罗·萨缪尔森(Paul Samuelson)表示,许多数学家已经开发出对经济学家有用的方法,但冯·诺依曼在对经济理论本身做出重大贡献方面是独一无二的。[96]
冯·诺依曼那篇著名的 9 页论文最初是在普林斯顿的一次演讲,后来成为一篇德文论文,最后被翻译成英文。他对经济学的兴趣导致了这篇论文的发表。1928 年和 1929 年在柏林讲课期间,他回到布达佩斯的家中度过了暑假,经济学家尼古拉斯·卡尔多也是如此,他们合得来。卡尔多建议冯·诺依曼读一本数学经济学家里昂·瓦尔拉斯的书。冯·诺依曼在那本书里发现了一些错误并加以纠正,例如,用不等式代替方程。他注意到,导致联立线性方程组的瓦尔拉斯一般均衡理论和瓦尔拉斯定律可能会产生荒谬的结果,即通过生产和销售负数量的产品可以使利润最大化。他用不等式代替了方程,引入了动态平衡,等等,并最终发表了这篇论文。[97]
3.11 线性规划
基于对矩阵对策和他的扩张经济模型的研究成果,冯·诺伊曼又发明了线性规划中的对偶理论。在乔治·丹齐格用几分钟描述了他的研究工作之后,冯·诺依曼不耐烦地要求他开门见山。然后,丹齐格目瞪口呆地听着冯·诺依曼作了一个小时的关于凸集、不动点理论和对偶的讲座,推测矩阵对策和线性规划之间的等价性。[98]
后来,冯·诺依曼提出了一种新的线性规划方法,使用了戈丹的齐次线性系统(1873 年),这种方法后来被卡尔马尔卡算法推广开来。冯·诺依曼的方法使用了单形之间的绕轴旋转算法,绕轴旋转的决策由一个具有凸性约束的非负最小二乘子问题决定(将零向量投影到活动单纯形的凸包上)。冯·诺依曼算法是线性规划的第一个内点法。[98]
3.12 数理统计
冯·诺依曼对数理统计做出了根本性贡献。1941 年,他导出了独立和相同正态分布变量的连续差的均方与样本方差之比的精确分布。[99] 这个比率应用于回归模型的残差,通常被称为杜宾-沃森统计[100] 用于测试零假设,即误差与它们遵循平稳的一阶自回归的替代值是连续独立的。[100]
随后,丹尼斯·萨甘和阿洛克·巴尔加瓦将测试结果扩展到回归模型的误差是否遵循高斯随机游走(即拥有单位根),而非它们是平稳的一阶自回归这一结果。[101]
3.13 流体动力学
冯·诺依曼在流体动力学领域做出了根本性的贡献。
冯·诺伊曼(Von Neumann)对流体动力学的贡献包括他发现了冲击波经典流解决方案,[102]以及与 Yakov borisovich Zeldovich 和 Werner Dring 共同发现了炸药 ZND 爆轰模型(Yakov Borisovich Zel'dovich 和 Werner Dring 都各自在该领域进行独立研究)[103]。20 世纪 30 年代,冯·诺依曼成为聚能数学的权威。[104]
后来,冯·诺依曼和罗伯特·里奇迈尔一起开发了一种定义人工粘性的算法,这种算法提高了对冲击波的理解。当计算机解决流体力学或空气动力学问题时,他们试图在尖锐的不连续区域(冲击波)放置太多的计算网格点。人工粘度的数学算法在不牺牲基础物理的情况下平滑了冲击转变。[105]
冯·诺依曼很快将计算机建模应用于该领域,为他的弹道研究开发软件。第二次世界大战期间,有一天他来到美国陆军弹道研究实验室主任 R.H .肯特的办公室,带着一个他为计算模拟冲击波的 100 个分子的一维模型而创建的计算机程序。冯·诺依曼随后给包括他的朋友西奥多·冯·卡门在内的听众举办了一个关于他的计算机程序的研讨会。冯·诺依曼讲完后,冯·卡门说:“约翰尼,这很有趣。你当然知道拉格朗日也使用数字模型来模拟连续介质力学。” 从冯·诺依曼的脸上可以明显看出,他还不了解拉格朗日的力学分析。[106]
3.14 数学大师
斯坦·乌兰非常了解冯·诺依曼,他这样描述自己对数学大师的认识:“大多数数学家都知道一种方法。例如,诺伯特·维纳已经掌握了傅立叶变换。一些数学家已经掌握了两种方法,可能会给只知道其中一种方法的人留下深刻印象。约翰·冯·诺依曼已经掌握了三种方法。” 他接着解释说,这三种方法是:
- 用符号操纵线性算子的工具;
- 对任何新数学理论的逻辑结构的直觉;
- 对新理论组合上层建筑的直觉。[107]
爱德华·泰勒写道,“没有人知道所有的科学,甚至冯·诺依曼也不知道。但在数学方面,除了数论和拓扑学,他对它的每一部分都有贡献。我认为,他是独一无二的。”[108]
冯·诺伊曼被要求为门外汉写一篇文章,描述数学是什么,并做了一个漂亮的分析。他解释说,数学跨越了经验和逻辑之间的世界,认为几何原本是经验的,但欧几里德构建了一个逻辑演绎理论。然而,他认为,总有偏离现实世界太远,变成无关紧要的诡辩的危险。[109][110][111]
4. 核武器
4.1 曼哈顿计划
从 20 世纪 30 年代末开始,冯·诺依曼发展了爆炸方面的专业知识——这种现象很难用数学方法建模。在此期间,冯·诺依曼是聚能数学的主要权威。这使他介入了大量军事咨询服务,主要是为海军服务,这使他有机会参与了曼哈顿计划。其中包括经常坐火车去新墨西哥州偏远地区洛斯阿拉莫斯实验室的项目秘密研究设施。[112]
冯·诺依曼对原子弹的主要贡献在于爆炸透镜的概念和设计,这些透镜是压缩后来投放到长崎的胖子武器钚芯所必需的。虽然冯·诺依曼并不是 “内爆” 概念的创始人,但他是这个概念最坚定的支持者之一,他鼓励这个概念继续发展,这跟他的许多同事的直觉是相违背的,他们觉得这样的设计是行不通的。他最终还想出了使用更强大的聚能装药和更少的裂变材料来大大提高 “组装” 速度的想法。[112]
当发现铀-235 不足以制造一枚以上的炸弹时,内爆透镜项目大大扩展,冯·诺依曼的想法得以实现。内爆是唯一可以用于汉福德工厂钚-239 的方法。[113]他确定了所需爆炸透镜的设计,但仍存在对炸药 “边缘效应” 和缺陷的担忧。[114]他的计算表明,如果内爆与球形对称的偏离不超过 5%,内爆就会发生。[115]在一系列模型尝试失败后,乔治·基斯提科夫斯基(George Kistiakowsky)实现了这一目标,三一炸弹的建造于 1945 年 7 月完成。[116]
冯·诺伊曼(von Neumann)在 1944 年 9 月对洛斯阿拉莫斯的一次访问中表明,如果冲击波的入射角在 90°和某个极限角之间,那么固体物体的爆炸冲击波反射产生的压力增加要比以前认为的大。因此,人们确定原子弹的效能将随着爆炸在目标上方几公里处而不是在地面上而得到增强。[117][118]
冯·诺伊曼(Von Neumann)、另外四名科学家和多名军事人员都被列为目标选择委员会的一员,该委员会负责选择日本广岛和长崎作为第一颗原子弹的爆炸目标。冯·诺伊曼负责监督与炸弹爆炸的预期规模、估计死亡人数以及炸弹爆炸时离地面的距离有关的计算,以获得最佳冲击波传播,从而达到最大杀伤效果。文化之都京都作为备选的军事重镇目标避免了遭到轰炸,本来它是冯·诺依曼的第一选择,[119]曼哈顿计划领导人莱斯利·格罗夫斯将军也附议了这一选择。然而,这一目标提议最后被战争部长亨利·史汀生驳回。[120]
1945 年 7 月 16 日,冯·诺伊曼和许多其他曼哈顿项目人员目睹了代号为三一的原子弹爆炸的第一次试验。该试验是在新墨西哥州索科罗东南 35 英里(56 公里)的阿拉莫戈多陆军机场附近的爆炸范围内作为内爆方法装置的测试进行的。仅根据他的观察,冯·诺伊曼估计这次试验导致了相当于 5 千吨梯恩梯(21 万亿焦耳)的爆炸,但恩利克·费密通过在冲击波经过他的位置时扔下碎纸片,观察它们分散的程度,得出了更准确的 10 千吨的估计。爆炸的实际威力在 20 到 22 千吨之间。[121]正是在冯·诺伊曼 1944 年的论文中,“千吨” 这个词首次出现。[122]战后,罗伯特·奥本海默评论说,参与曼哈顿计划的物理学家们 “知道罪恶”。冯·诺伊曼的回答是,“有时有人承认一项罪行,以此来获得荣誉。”[123]
冯·诺伊曼在工作中继续保持镇定,并和爱德华·泰勒一起成为氢弹项目的支持者之一。他与克劳斯·福克斯合作进一步发展原子弹,两人在 1946 年提交了一份关于 “利用核能的方法和手段的改进” 的秘密专利,该专利概述了使用裂变炸弹压缩聚变燃料以引发核聚变的方案。[124]富克斯-冯·诺依曼的专利使用了辐射内爆,但方式不同于后来的氢弹设计——泰勒-乌兰设计。然而,他们的工作被纳入了 “乔治” 拍摄的 “温室行动” 的镜头,这对测试最终设计中的概念具有指导意义。[125]富克斯-冯·诺依曼的研究成果被富克斯作为其核间谍活动的一部分传给了苏联,但它并没有用于苏联自己独立开发的泰勒-乌兰设计。历史学家杰里米·伯恩斯坦嘲讽地指出,“约翰·冯·诺依曼和克劳斯·福克斯在 1946 年发明了一项辉煌的发明,这项发明本可以改变氢弹的整个发展过程,但直到成功制造出氢弹后才被完全理解。”[125]
冯·诺伊曼因其战时杰出服务,于 1946 年 7 月被授予海军杰出民用服务奖,并于 1946 年 10 月被授予荣誉勋章。[126]
4.2 原子能委员会
1950 年,冯·诺伊曼成为武器系统评估小组(WSEG)的顾问,[127]该小组的职能是就新技术的开发和使用向参谋长联席会议和美国国防部长提供咨询。[128]他还成为武装部队特别武器项目(AFSWP)的顾问,该项目负责核武器的军事方面。在接下来的两年里,他成为了中央情报局(CIA)的顾问、原子能委员会有影响力的总咨询委员会的成员、新成立的劳伦斯·利弗莫尔国家实验室的顾问,以及美国空军科学咨询小组的成员。[127]
1955 年,冯·诺伊曼成为原子能委员会(AEC)的委员。他接受了这一职位,并利用这一职位进一步生产适合洲际弹道导弹运载的小型氢弹。他致力于纠正这些小型武器所需氚和锂 6 的严重短缺,并反对满足陆军的中程导弹需求。他坚持认为用洲际弹道导弹(ICBM)发射到敌方领土中心的氢弹将是最有效的武器,而且氢弹的相对误差不会成为问题。他说俄罗斯人可能会建造一个类似的武器系统,事实证明就是这样。[129][130] 尽管他和奥本海默在开发氢弹的应急计划的必要性上意见不一,但他还是在 1954 年的奥本海默安全听证会上代表奥本海默作证,在听证会上,他坚称奥本海默是忠诚的,并赞扬了他在该计划实施后的帮助。[131]
冯·诺伊曼死于癌症前不久,曾领导了美国政府的最高机密洲际弹道导弹(ICBM)委员会,该委员会有时会在他家里开会。其目的是决定建造一个大到足以携带热核武器的洲际弹道导弹的可行性。冯·诺伊曼长期以来一直认为,虽然技术障碍是相当大的,但它们可以及时克服。SM-65 阿特拉斯导弹在他去世两年后,于 1959 年通过了第一次全功能测试。洲际弹道导弹的可行性既归功于火箭技术的发展,也归功于改进后的更小弹头,他对前者的理解使他的建议变得弥足珍贵。[131]
4.3 相互保证毁灭
冯·诺伊曼被誉为发展了相互保证毁灭(MAD)的平衡战略。他还 “感动天地” 来促成 MAD。他的目标是迅速开发洲际弹道导弹和小型氢弹,这个想法可以让苏联人知道,他知道苏联也在做类似的工作,因为中央情报局采访了被允许返回德国的德国火箭科学家,冯·诺伊曼在中央情报局安插了十几名技术人员。苏联认为轰炸机很快就会不堪一击,他们同意冯·诺依曼的观点,洲际弹道导弹中的氢弹是核武器中的超级炸弹;他们相信,无论谁在这些武器上拥有优势,都将接管世界,而不一定使用它们。[132]他害怕 “导弹实力的差距”,并采取了更多的行动来实现与苏联保持一致的目标:
- 他修改了 ENIAC,使其可编程,然后为其编写程序进行氢弹计算,验证泰勒乌拉姆设计是可行的,并进一步发展它。
- 通过原子能委员会,他推动了一种小型氢弹的开发,这种氢弹可以安装在洲际弹道导弹上。
- 他亲自出面协调,以加快紧凑型炸弹所需的锂-6 和氚的生产。
- 他促成了几个独立的导弹项目的启动,因为他觉得竞争与合作相结合能获得最好的结果。[133]
冯·诺依曼关于苏联在导弹技术方面领先的评估在当时被认为是悲观的,但很快在人造卫星危机中被证明是正确的。[134]
冯·诺伊曼进入政府部门服务主要是因为他认为,如果自由和文明要生存下去,美国就必须要战胜纳粹主义、法西斯主义和苏联共产主义的极权主义。在一次参议院委员会听证会上,他将自己的政治意识形态描述为 “暴力反共,比正常情况更加军国主义”。引用他 1950 年的话,“如果你说为什么明天不轰炸(苏联),我会说,为什么今天不轰炸?如果你说今天五点轰炸,我会说为什么不是一点呢?”[135]
1956 年 2 月 15 日,冯·诺依曼被德怀特·戴维·艾森豪威尔总统授予自由勋章。他的引文写道:
冯·诺伊曼博士在一系列具有重大国家意义的科学研究项目中,极大地促进了国家在军备领域的科学进步。
冯·诺伊曼博士通过他在美国大陆以外执行的各种高度机密的任务以及极其重要的国际项目,解决了国防领域一些最困难的技术问题。
5. 计算
冯·诺依曼是计算机领域的创始人。[136]1945 年,冯·诺伊曼发明了归并排序算法,在该算法中,数组的前半部分和后半部分分别递归排序,然后合并。[137][138]冯·诺伊曼用墨水笔为 EDVAC 写了 23 页长的排序程序。在第一页上,仍然可以看到 “绝密” 这个短语的痕迹,这个短语是用铅笔写的,后来被擦掉了。[138]艾伦·图灵在 20 世纪 30 年代访问普林斯顿时,冯·诺伊曼也和他一起研究人工智能哲学。[139]
冯·诺依曼的氢弹研究工作是在计算领域完成的,他和斯塔尼肖·乌兰在冯·诺依曼的数字计算机上模拟了流体力学计算。在此期间,他对蒙特卡罗方法的发展作出了贡献,蒙特卡罗方法允许用随机数类似复杂问题的解决方案。[140]
冯·诺依曼用带偏性掷币模拟公平硬币的算法被用在一些硬件随机数发生器的 “软件白化” 阶段。[141]因为使用 “真正的” 随机数列表非常慢,冯·诺依曼开发了一种利用平方取中法制作伪随机数的方法。尽管这种方法被批评为粗糙,但冯·诺伊曼意识到了这一点:他认为它比他所能使用的任何其他方法都要快,并写道,“任何考虑用算术方法产生随机数字的人,当然都处于罪恶的状态。”[142]冯·诺伊曼还指出,当这种方法出错时,是显而易见的,不像其他方法那样可能是微妙的错误。[142]
冯·诺伊曼在为宾夕法尼亚大学摩尔电气工程学院进行离散变量自动电子计算机(EDVAC))项目提供咨询时,写了一份不完整的 EDVAC 报告初稿。该报告的过早曝光使 EDVAC 设计者埃克特和莫克利的专利申请无效,该报告描述了一种计算机架构,其中数据和程序都存储在同一地址空间的计算机存储器中。这种架构是大多数现代计算机设计的基础,不同于最早使用独立存储设备(如纸带或插板)进行 “编程” 的计算机。尽管由于冯·诺依曼的论文,单存储器存储程序架构通常被称为冯·诺依曼架构,但该架构是基于宾夕法尼亚大学 ENIAC 计算机的发明者埃克特和毛奇利的研究成果。[143]
作为科学咨询委员会的成员,约翰·冯·诺依曼为陆军弹道研究实验室提供咨询,其中最著名的就是 ENIAC 项目[144][145]。新 ENIAC 的电子设备以六分之一的速度运行,但这丝毫没有降低 ENIAC 的性能,因为它仍然完全受输入/输出(I/O)限制。复杂的程序可以在几天内开发和调试,而不是象在旧的 ENIAC 插接板上需要几个星期才能完成。冯·诺依曼早期的一些计算机程序被保存了下来。[146]
冯·诺依曼设计的下一台计算机是新泽西州普林斯顿高等研究所的 IAS 机器。他安排了所需资金,在附近的皇家航空公司(RCA)研究实验室设计和建造了组件。约翰·冯·诺依曼建议绰号为防御计算机的 IBM 701 应该包括一个磁鼓。这是 IAS 机器的一个更快的版本,并为商业上成功的 IBM 704 奠定了基础[147] [148]
冯·诺依曼在 1953 年的一篇开创性论文中首次介绍了随机计算。[149]然而,这一理论直到 20 世纪 60 年代计算机技术的进步才得以实现。[150][151]
5.1 细胞自动机、脱氧核糖核酸 DNA 和通用构造函数
冯·诺伊曼对自我复制结构(构造者、描述和被构造者之间的符号关系)的严格数学分析先于脱氧核糖核酸结构 DNA 的发现。[152]
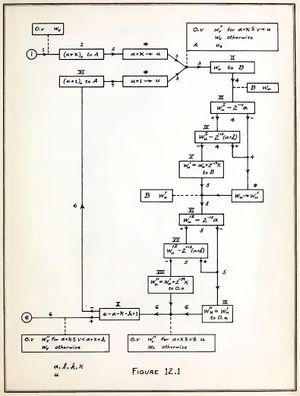
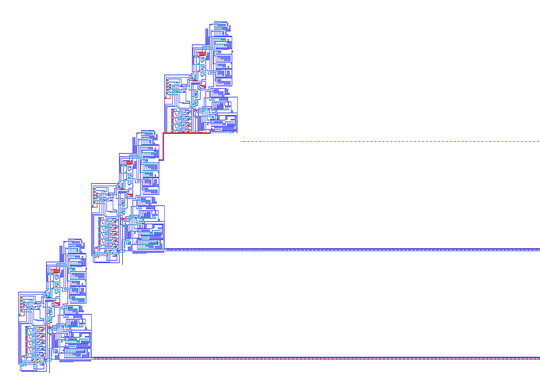
冯·诺伊曼(Von Neumann)在没有计算机帮助的情况下创造了细胞自动机领域,用铅笔和图表纸构建了第一个自我复制的自动机。
1948 年和 1949 年冯·诺依曼在演讲中首次提出了物理非生物自我复制系统的详细建议,当时他仅首次提出了运动学自我复制自动机。[153][154] 虽然定性的看是合理的,但冯·诺依曼显然不满意这种自我复制者的模型,因为很难用数学严密性来分析它。相反,他基于细胞自动机的原始概念,开发了一个更抽象的模型——自我复制器。[155]
随后,基于冯·诺依曼元胞自动机的冯·诺伊曼通用构造函数的概念,在他死后出版的《自我复制自动机理论》一书中得到充实。乌兰和冯·诺依曼在 20 世纪 50 年代创造了一种计算液体运动的方法。该方法的驱动概念是将液体视为一组离散单元,并根据其邻居的行为计算每个单元的运动[156]。像 Ulam 的晶格网络一样,冯·诺依曼的细胞自动机也是二维的,他的自我复制器是用算法实现的。结果是一个通用的复印机和构造器在一个小邻域的细胞自动机中工作(只有那些接触的细胞才是邻域;对于冯·诺伊曼的细胞自动机,只有正交细胞),每个细胞有 29 个状态[157]。冯·诺依曼通过设计一个 200,000 个细胞的结构,证明了一个存在性,即一个特定的模式会在给定的细胞宇宙中产生无限复制。[157]
这里存在一个临界尺寸,在这个临界尺寸以下,合成的过程是逐渐退化的,但是在这个临界尺寸以上,合成的现象,如果适当地安排,可以变成爆炸性的,换句话说,自动机的合成可以以这样一种方式进行,即每个自动机将产生比它自己更复杂和潜力更大的其他自动机。
冯·诺依曼谈到了他的自我复制机器中复杂性的进化增长[158]。他的 “原理验证” 设计表明,通过使用一个通用可编程(“通用”)构造器,逻辑上是如何让展示一个无限大类的自我复制成为可能,跨越一个广泛的复杂性,通过一个潜在的突变路径网络相互连接,包括从最简单到最复杂的路径。这是一个重要的结果,因为在此之前,人们或许认为,这种途径的存在有一个基本的逻辑障碍;在这种情况下,支持这种途径的生物有机体不可能是传统意义上的 “机器”。冯·诺伊曼考虑了他的自复制机器之间的潜在冲突,指出 “我们的模型导致了这样的冲突情况”[159],表明它是一个有待进一步研究的领域。
控制论运动强调了自我复制需要什么才能自动发生的问题,1952 年,约翰·冯·诺依曼设计了一种精巧的 2D 细胞自动机,可以自动复制细胞的初始结构。[160]冯·诺伊曼邻域继续用于其他细胞自动机,在该邻域中,二维网格中的每个细胞具有四个正交相邻的网格细胞作为邻居。冯·诺伊曼证明,进行大规模采矿作业(如开采整个月球或小行星带)的最有效方法是利用它们的指数增长,使用自我复制的航天器。[161]
冯·诺依曼研究了在数字计算机上模拟进化是否能解决编程中的复杂性问题。[159]
从 1949 年开始,冯·诺依曼(von Neumann)设计的自我复制计算机程序被认为是世界上第一个计算机病毒,他被认为是计算机病毒学理论之父。[162]
5.2 天气系统和全球变暖
作为天气预报研究的一部分,冯·诺依曼于 1946 年在普林斯顿创立了 “气象项目”,并从美国海军获得了该项目的资金[163]。冯·诺伊曼和他在这个项目上任命的助手朱莉·格雷戈里·查尼(Jule Gregory Charney)编写了世界上第一个气候建模软件,并利用它在 ENIAC 计算机上进行了世界上第一次数值天气预报[163];冯·诺依曼和他的团队在 1950 年发表了正压涡度方程的数值积分结果[164]。他们一起在将海气能量和水分交换纳入气候研究的努力中发挥了主导作用[165]。冯·诺伊曼(Von Neumann)提出了气候建模的研究计划:“这种方法首先尝试短期预测,然后对那些能够在任意长的时间内持续存在的环流特性进行长期预测,最后才尝试对中长期的气候变化进行预测,这些预测时间因为太长而无法用简单的流体动力学理论来处理,而太短则又无法用平衡理论的一般原理来处理[166]。”
冯·诺伊曼对天气系统和气象预测的研究促使他提出通过在极地冰盖上散布着色剂来提高太阳辐射的吸收(通过降低反射率)[167][168],引起全球变暖,从而控制环境[167][168]。冯·诺伊曼提出了一个关于人类活动导致全球变暖的理论,指出地球在最后一次冰河时期只冷 6 华氏度(3.3 摄氏度),他在 1955 年写道:“工业燃烧煤和石油释放到大气中的二氧化碳——在上一代超过一半——可能已经改变了大气的组成,足以解释全球普遍变暖大约 1 华氏度的原因。” 当然,能做什么并不代表一定应该做什么[169][170],然而,冯·诺伊曼还是敦促人们对任有可能对人类天气带来影响的项目保持一定程度的谨慎……事实上,评估全面变冷或全面变热的最终结果将是一件复杂的事情。这些变化将影响海平面升高和降低,从而影响沿海大陆架的可居住性;海洋的蒸发,以及由此产生的一般降水和结冰的程度;等等……但毫无疑问,人们可以进行预测结果所需的必要分析,以任何期望的规模进行干预,最终取得相当出色的结果[170]。”
"现在正在发展并将在未来几十年占据主导地位的技术与传统的、基本上暂时仍然有效的地理和政治单位和概念相冲突。这是一场成熟的技术危机……最有希望的答案是,人类物种以前曾经历过类似的测试,在经历了各种各样的困难后,它似乎有一种先天的能力来克服这种冲突。"
——冯·诺伊曼,1955 年 [170]
5.3 技术奇异性假设
“奇点” 概念在技术领域的首次应用归功于冯·诺依曼[171],他根据乌兰的说法,讨论了 “技术的不断加速进步和人类生活方式的变化,这给人的印象是,人类历史上正在出现某种本质上的奇点,我们所知的人类事务在这种奇点之外无法继续下去。”[172]这一概念后来在阿尔文·托夫勒的《未来冲击》一书中得到充实。
6. 认知能力
其他数学家对冯·诺依曼在头脑中瞬间完成复杂运算的能力感到震惊。[173]当他六岁的时候,他可以在脑子里除两个八位数,并用古希腊语交谈。[174]当他 15 岁被送到分析师加博尔·Szegő手下学习高等微积分时,szegő对这个男孩的数学天赋感到震惊,以至于他们第一次见面时他就激动地哭了。[175]
诺贝尔奖获得者汉斯·贝特说 “我有时想知道冯·诺依曼的大脑是否表明一个优于人类的物种”[175],后来贝特写道 “冯·诺依曼的大脑表明一个新物种,一个超越人类的进化”[175]。尤金·维格纳写道,“看到冯·诺依曼的大脑在工作,人们就会有这样一种印象:这是一台完美的仪器,它的齿轮被加工成精确啮合千分之一英寸[176]。” 保罗·哈尔莫斯说,“冯·诺依曼的速度令人敬畏。[177]” 伊斯雷尔·哈尔佩林说:“跟上他的步伐是……不可能的。感觉就像你骑着三轮车追逐一辆赛车[177]。” 爱德华·泰勒承认他 “永远跟不上他”[177]。泰勒还说,“冯·诺依曼会和我 3 岁的儿子进行一次谈话,他们两个会平等地交谈,我有时想知道他和我们其他人交谈时是否使用了同样的原则。[178]” 彼得·拉克斯(Peter Lax)写道,“冯·诺依曼沉迷于思考,尤其是对数学的思考[179]。
当乔治·丹齐格给冯·诺依曼带来一个线性规划中尚未解决的问题(就像我给普通人带来的一样),这个问题还没有发表过任何文献,他惊讶地发现,当冯·诺依曼说 “哦,那个!” 之后,就即席发表一个多小时的演讲,解释如何使用迄今为止尚未理解的对偶理论来解决这个问题。[180]
洛塔尔·沃尔夫冈·诺德海姆将冯·诺依曼描述为 “我见过的思维最敏捷的人”[173],雅各布·布罗诺斯基写道 “他是我所认识的最聪明的人,毫无例外。他是个天才。[181]” 乔治·派尔亚曾在苏黎世联邦理工学院举办讲座,冯·诺伊曼以学生身份参加,乔治说:“约翰尼是我唯一害怕的学生。如果在讲座过程中我陈述了一个未解决的问题,那么他很可能会在讲座结束时带着写在纸条上的完整解决方案来找我[182]。” 尤金·维格纳写道:“‘简西’,我可能会说,‘角动量总是 h 的整数吗?’一天后,他会带着肯定的回答回来:“是的,如果所有粒子都处于静止状态……我们都敬畏简西·冯·诺依曼”[183]。恩利克·费密告诉物理学家赫伯特·安德森:“你知道吗,赫伯特,约翰尼在脑子里的运算速度是我的十倍!我可以以你十倍的速度完成,赫伯,所以你看约翰尼有多了不起[184]!"
霍尔姆斯讲述了尼古拉斯·米特罗波尼斯(Nicholas Metropolis)讲述的一个故事,关于冯·诺依曼的计算速度,当时有人要求冯·诺依曼解决著名的苍蝇之谜(飞行难题):[185]
两个骑自行车的人开始相距 20 英里,彼此相向,各自以每小时 10 英里的稳定速度前进。与此同时,一只苍蝇以 15 英里/小时的稳定速度,从向南行的自行车的前轮开始,飞到向北行的自行车的前轮,然后转过身,再次飞到向南行的自行车的前轮,并以这种方式继续飞行,直到他在两个前轮之间被压碎。问:这只苍蝇飞了多远?找到答案的最慢方法是计算苍蝇在旅程的第一段、南行、第二段、北行、第三段等距离。等等。最后,对如此获得的无穷级数求和。
最快的方法是观察自行车出发后正好一个小时相遇,这样苍蝇就只有一个小时的时间旅行;因此答案肯定是 15 英里。
当这个问题被问及冯·诺依曼时,他立刻就解决了,从而让提问者失望:“哦,你一定听过这个把戏!”“什么把戏?” 冯·诺依曼问道,“我所做的只是对几何级数求和。”
尤金·维格纳讲了一个类似的故事,只是用燕子代替了苍蝇,他说是梅克斯·玻恩在 20 世纪 20 年代向冯·诺伊曼提出了这个问题[186]。冯·诺依曼还以他异常清晰的记忆(有时也称为过目不忘)而闻名。赫尔曼·戈德斯汀写道:
他非凡的能力之一是他的绝对记忆力。据我所知,冯·诺依曼对于曾经读过一本书或一篇文章,可以逐字引用;更令人称奇的是,几年后他还可以毫不犹豫地做到这一点。他也可以毫不减速地把它从原来的语言翻译成英语。有一次,我要求他告诉我《双城记》是如何开始的,以此来测试他的能力。于是,没有任何停顿,他立即开始背诵第一章,并持续到大约十分钟或十五分钟后被要求停止。
据报道,冯·诺依曼能够记住电话簿每页的电话号码。他通过让朋友随机调出页码来娱乐他们;然后他背诵了其中的名字、地址和数字。[175][187]
7. 数学遗产
“公平地说,如果一个科学家的影响足够宽泛,包括对科学本身以外领域的产生影响,那么约翰·冯·诺依曼可能是有史以来最有影响力的数学家,” 米克尔洛斯·雷迪在《约翰·冯·诺依曼:书信选集》中写道[188]。詹姆斯·格列姆写道:“他被认为是现代数学的巨人之一”[189]。数学家让·迪厄多内说,冯·诺依曼 “可能是曾经欣欣向荣的众多群体中的最后一个代表,这些伟大的数学家在纯数学和应用数学方面都同样如鱼得水,并且在他们的职业生涯中在两个方向上都保持着稳定的成果”[190],而彼得·拉克斯则形容他拥有 “本世纪最聪明的才智”[190]。彼得·拉克斯在米克尔斯·雷迪的《书信选集》的前言中写道:“要衡量冯·诺依曼的成就,考虑到如果他能正常多活几年,他肯定会获得诺贝尔经济学奖。如果有计算机科学和数学方面的诺贝尔奖,他也会因此而获奖。因此,这些信的作者应该被认为是因为他在物理,特别是量子力学方面的工作,而三次获得诺贝尔奖,或者可能三次半获得诺贝尔奖的人”。[191]
8. 疾病和死亡
1955 年,冯·诺依曼被诊断患有骨癌或胰腺癌[192]。他无法接受自己濒临死亡的现实,即将死亡的阴影给了他巨大的恐惧[193]。他邀请了一位罗马天主教神父安塞尔姆·斯特里赫特马特神父来拜访他进行咨询[194]。据报道,冯·诺伊曼说,“只要不信教的人有可能受到永久的诅咒,那么最终成为一个信教的人就更合乎逻辑”,帕斯卡的赌注本质上是有道理的。他早些时候向母亲吐露说,“可能一定有上帝。有比没有更容易解释事情。[194][195][196] ” 斯特里赫特神父为他主持最后的仪式[194]。冯·诺依曼的一些朋友(如亚伯拉罕·派斯和奥斯卡·莫根施特恩)说,他们一直认为他是 “完全不可知论者”。对于这种临终前的皈依,摩根斯坦告诉海姆,[195][197] “他一生当然完全是不可知论者,然后他突然变成了天主教徒——这与他健康时的态度、观点和思维完全不一致。”[198]斯特里赫特神父回忆说,即使在他皈依后,冯·诺依曼也没有从中获得多少安宁或安慰,因为他仍然害怕死亡。[198]
冯·诺伊曼临终时,他用心逐字背诵歌德《浮士德》每页的前几行,以此来娱乐他的兄弟[199]。他于 1957 年 2 月 8 日在华盛顿特区沃尔特里德陆军医疗中心去世,享年 53 岁,当时他处于军事安全状态,以免在服用大量药物时泄露军事秘密。他被安葬在新泽西州默瑟县普林斯顿的普林斯顿公墓。
9. 荣誉
- 运筹学和管理科学研究所(INFORMS 以前叫 TIMS—ORSA)的约翰·冯·诺依曼理论奖每年授予在运筹学和管理科学理论方面做出基础和持续贡献的个人(或团体)。[200]
- 电气和电子工程师协会(IEEE)每年都会颁发 “电气和电子工程师协会约翰·冯·诺依曼奖章”,以表彰在计算机相关科学和技术方面的做出杰出成就人士。[201]
- 约翰·冯·诺依曼讲座每年由一位对应用数学有贡献的研究人员在工业和应用数学协会举办,被选中的讲师还会获得一笔奖金。[202]
- 月球上的冯·诺依曼陨石坑是以他的名字命名的。[203]
- 小行星 22824 冯·诺依曼以他的名字命名。[204][205]
- 新泽西普兰斯伯罗镇的约翰·冯·诺依曼中心以他的名字命名。[206]
- 匈牙利计算机科学家专业协会,约翰·冯·诺依曼计算机协会,是以约翰·冯·诺依曼的名字命名的[207]。它于 1989 年 4 月关闭。[208]
- 2005 年 5 月 4 日,美国邮政发行了美国科学家纪念邮票系列,这是一套由艺术家维克多·斯塔宾(Victor Stabin)设计的四枚 37 美分的不干胶邮票,有几种构型。描绘的科学家是冯·诺伊曼、芭芭拉·麦克林托克、乔赛亚·威拉德·吉布斯和理查德·费曼。[209]
- 拉伊克·拉斯洛高等研究学院的约翰·冯·诺依曼奖是以他的名字命名的,自 1995 年以来,每年都颁发给那些对精确的社会科学做出杰出贡献并通过他们的工作对学院成员的专业发展和思维产生重大影响的教授。[210]。
- 约翰·冯·诺依曼大学于 2016 年在匈牙利成立,接替凯克斯特学院。[211]
10. 著作
- 1923.关于超限数的介绍,346–54。
- 1925.集合论的公理化,393–413。
- 1932.量子力学的数学基础。普林斯顿大学出版社。1996 年版:ISBN 0-691-02893-1。
- 1937.约翰·冯·诺依曼(1981)。以色列哈尔佩林(编辑)。)。具有转移概率的连续几何。美国数学学会回忆录。34.ISBN 978-0-8218-2252-4。MR0634656。
- 1944.《博弈论与经济行为》,与摩根斯坦合著,普林斯顿大学出版社,archive.org 在线。2007 年版:ISBN 978-0-691-13061-3。
- 1945.离散变量自动电子计算机(EDVAC)报告初稿
- 1948.“自动机的一般逻辑理论”,载于《行为中的大脑机制:希克森研讨会》,杰弗里斯,洛杉矶编辑。约翰·威利父子公司,纽约,纽约,1951 年,第 1-31 页,MR 0045446。
- 1960.约翰·冯·诺伊曼(1998)。连续几何。普林斯顿数学地标。普林斯顿大学出版社。ISBN 978-0-691-05893-1。MR 0120174。
- 1963.约翰·冯·诺依曼全集,陶博,A·H 编辑。,佩格蒙出版社。ISBN 0-08-009566-6
- 1966.自复制自动机理论。博克斯 A·W 编辑,伊利诺伊大学出版社。ISBN 0-598-37798-0[212]
11. 笔记
- Dempster, M. A. H. (February 2011). "Benoit B. Mandelbrot (1924–2010): a father of Quantitative Finance" (PDF). Quantitative Finance. 11 (2): 155–156. doi:10.1080/14697688.2011.552332.
- p. 3.
- p. 90.
- p. 8.
- p. 1. Myhrvold, Nathan (March 21, 1999). "John von Neumann". Time.
- p. 104.
- p. xxi.
- pp. 38–42.
- pp. 37–38.
- p. 39.
- pp. 44–45.
- pp. 57–58.
- p. 30.
- p. 28.
- p. 124.
- pp. 46–47.
- Halmos, P. R. (1973). "The Legend of von Neumann". The American Mathematical Monthly. 80 (4): 382–394. doi:10.2307/2319080. JSTOR 2319080.
- p. 90.
- p. 52.
- pp. 70–71.
- p. 3.
- pp. 32–33.
- p. 5.
- p. 81.
- p. 84.
- von Kármán, T., & Edson, L. (1967). The wind and beyond. Little, Brown & Company.
- pp. 85–87.
- p. 97.
- Regis, Ed (November 8, 1992). "Johnny Jiggles the Planet". The New York Times. Retrieved February 4, 2008.
- von Neumann, J. (1928). "Die Axiomatisierung der Mengenlehre". Mathematische Zeitschrift (in German). 27 (1): 669–752. doi:10.1007/BF01171122. ISSN 0025-5874.CS1 maint: Unrecognized language (link)
- pp. 86–87.
- The Collected Works of Eugene Paul Wigner: Historical, Philosophical, and Socio-Political Papers. Historical and Biographical Reflections and Syntheses, By Eugene Paul Wigner, (Springer 2013), page 128
- pp. 98–99.
- Hashagen, Ulf (2010). "Die Habilitation von John von Neumann an der Friedrich-Wilhelms-Universität in Berlin: Urteile über einen ungarisch-jüdischen Mathematiker in Deutschland im Jahr 1927". Historia Mathematica. 37 (2): 242–280. doi:10.1016/j.hm.2009.04.002.
- The History Of Game Theory, Volume 1: From the Beginnings to 1945, By Mary-Ann Dimand, Robert W Dimand, (Routledge, 2002), page 129
- p. 145.
- pp. 143–144.
- pp. 155–157.
- "Marina Whitman". The Gerald R. Ford School of Public Policy at the University of Michigan. 2014-07-18. Retrieved January 5, 2015.
- pp. 170–174.
- Bochner, S. (1958). "John von Neumann; A Biographical Memoir" (PDF). National Academy of Sciences. Retrieved August 16, 2015.
- pp. 43, 157.
- pp. 167–168.
- p. 371.
- pp. 195–196.
- pp. 190–195.
- p. 70.
- pp. 170–171.
- p. 103.
- "Conversation with Marina Whitman". Gray Watson (256.com). Archived from the original on April 28, 2011. Retrieved January 30, 2011.
- Poundstone, William (May 4, 2012). "Unleashing the Power". The New York Times.
- Blair, pp. 89–104.
- p. 150.
- p. 48.
- p. 94.
- Stern, Nancy (January 20, 1981). "An Interview with Cuthbert C. Hurd" (PDF). Charles Babbage Institute, University of Minnesota. Retrieved June 3, 2010.
- pp. 26–27.
- p. 75.
- pp. 393–394.
- pp. 104–105.
- p. 123.
- p. 70.
- p. 124.
- p. 182.
- von Neumann, J. (1929), "Zur allgemeinen Theorie des Masses" (PDF), Fundamenta Mathematicae, 13: 73–116, doi:10.4064/fm-13-1-73-116
- Two famous papers are: von Neumann, John (1932). "Proof of the Quasi-ergodic Hypothesis". Proc Natl Acad Sci USA. 18 (1): 70–82. Bibcode:1932PNAS...18...70N. doi:10.1073/pnas.18.1.70. PMC 1076162. PMID 16577432.. von Neumann, John (1932). "Physical Applications of the Ergodic Hypothesis". Proc Natl Acad Sci USA. 18 (3): 263–266. Bibcode:1932PNAS...18..263N. doi:10.1073/pnas.18.3.263. JSTOR 86260. PMC 1076204. PMID 16587674.. Hopf, Eberhard (1939). "Statistik der geodätischen Linien in Mannigfaltigkeiten negativer Krümmung". Leipzig Ber. Verhandl. Sächs. Akad. Wiss. 91: 261–304.
- Halmos, Paul R. (1958). "Von Neumann on measure and ergodic theory" (PDF). Bull. Amer. Math. Soc. 64 (3, Part 2): 86–94. doi:10.1090/S0002-9904-1958-10203-7.
- pp. 163–181.
- "Von Neumann Algebras" (PDF). Princeton University. Retrieved January 6, 2016.
- "Direct Integrals of Hilbert Spaces and von Neumann Algebras" (PDF). University of California at Los Angeles. Archived from the original (PDF) on 2015-07-02. Retrieved January 6, 2016.
- Van Hove, Léon (1958). "Von Neumann's Contributions to Quantum Theory". Bulletin of the American Mathematical Society. 64 (3): 95–99. doi:10.1090/s0002-9904-1958-10206-2.
- von Neumann, J. (1933). "Die Einfuhrung Analytischer Parameter in Topologischen Gruppen". Annals of Mathematics. 2. 34 (1): 170–179. doi:10.2307/1968347. JSTOR 1968347.
- "AMS Bôcher Prize". AMS. January 5, 2016. Retrieved 2018-01-12.
- *Neumann, John von (1936b), "Examples of continuous geometries", Proc. Natl. Acad. Sci. USA, 22 (2): 101–108, Bibcode:1936PNAS...22..101N, doi:10.1073/pnas.22.2.101, JFM 62.0648.03, JSTOR 86391, PMC 1076713, PMID 16588050
- Neumann, John von (1998) [1960], Continuous geometry, Princeton Landmarks in Mathematics, Princeton University Press, ISBN 978-0-691-05893-1, MR 0120174
- Neumann, John von (1962), Taub, A. H., ed., Collected works. Vol. IV: Continuous geometry and other topics, Oxford: Pergamon Press, MR 0157874
- Neumann, John von (1981) [1937], Halperin, Israel, ed., "Continuous geometries with a transition probability", Memoirs of the American Mathematical Society, 34 (252), doi:10.1090/memo/0252, ISBN 978-0-8218-2252-4, ISSN 0065-9266, MR 0634656
- p. 140.
- von Neumann, John (1930). "Zur Algebra der Funktionaloperationen und Theorie der normalen Operatoren". Mathematische Annalen (in German). 102 (1): 370–427. Bibcode:1930MatAn.102..685E. doi:10.1007/BF01782352.CS1 maint: Unrecognized language (link). The original paper on von Neumann algebras.
- Birkhoff, Garrett (1958). Von Neumann and lattice theory (PDF). Bulletin of the American Mathematical Society. 64. pp. 50–56. doi:10.1090/S0002-9904-1958-10192-5. ISBN 978-0-8218-1025-5.
- pp. 139–141.
- p. 142.
- Hermann, Grete (1935). "Die naturphilosophischen Grundlagen der Quantenmechanik". Naturwissenschaften. 23 (42): 718–721. Bibcode:1935NW.....23..718H. doi:10.1007/BF01491142. English translation in Hermann, Grete (2016). Crull, Elise; Bacciagaluppi, Guido, eds. Grete Hermann — Between physics and philosophy. Springer. pp. 239–278.
- Bell, John S. (1966). "On the problem of hidden variables in quantum mechanics". Reviews of Modern Physics. 38 (3): 447–452. Bibcode:1966RvMP...38..447B. doi:10.1103/RevModPhys.38.447.
- Bub, Jeffrey (2010). "Von Neumann's 'No Hidden Variables' Proof: A Re-Appraisal". Foundations of Physics. 40 (9–10): 1333–1340. arXiv:1006.0499. Bibcode:2010FoPh...40.1333B. doi:10.1007/s10701-010-9480-9.
- Mermin, N. David; Schack, Rüdiger (2018). "Homer nodded: von Neumann's surprising oversight". Foundations of Physics. 48 (9): 1007–1020. arXiv:1805.10311. Bibcode:2018FoPh...48.1007M. doi:10.1007/s10701-018-0197-5.
- Freire, Olival Jr. (2006). "Philosophy enters the optics laboratory: Bell's theorem and its first experimental tests (1965–1982)". Studies in History and Philosophy of Modern Physics. 37 (4): 577–616. arXiv:physics/0508180. Bibcode:2006SHPMP..37..577F. doi:10.1016/j.shpsb.2005.12.003.
- Wigner, Eugene; Henry Margenau (December 1967). "Remarks on the Mind Body Question, in Symmetries and Reflections, Scientific Essays". American Journal of Physics. 35 (12): 1169–1170. Bibcode:1967AmJPh..35.1169W. doi:10.1119/1.1973829.
- Schlosshauer, M.; Koer, J.; Zeilinger, A. (2013). "A Snapshot of Foundational Attitudes Toward Quantum Mechanics". Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics. 44 (3): 222–230. arXiv:1301.1069. Bibcode:2013SHPMP..44..222S. doi:10.1016/j.shpsb.2013.04.004.
- Kaplan, Michael and Kaplan, Ellen (2006) Chances are–: adventures in probability. Viking.
- Quantum Information Theory, By Mark M. Wilde, (Cambridge University Press 2013), page 252
- von Neumann, John (1927), "Wahrscheinlichkeitstheoretischer Aufbau der Quantenmechanik", Göttinger Nachrichten, 1: 245–272
- Schlüter, Michael and Lu Jeu Sham (1982), "Density functional theory", Physics Today, 35 (2): 36–43, Bibcode:1982PhT....35b..36S, doi:10.1063/1.2914933
- Ugo Fano (June 1995), "Density matrices as polarization vectors", Rendiconti Lincei, 6 (2): 123–130, doi:10.1007/BF03001661
- Dualism, Platonism and Voluntarism: Explorations at the Quantum, Microscopic, Mesoscopic and Symbolic Neural Levels, (Cambridge Scholars 2016), page 215
- Gabbay, Dov M.; Woods, John (2007). "The History of Quantum Logic". The Many Valued and Nonmonotonic Turn in Logic. Elsevier. pp. 205–2017. ISBN 978-0-08-054939-2.
- Birkhoff, Garrett; von Neumann, John (October 1936). "The Logic of Quantum Mechanics". Annals of Mathematics. 37 (4): 823–843. doi:10.2307/1968621. JSTOR 1968621.
- Putnam, Hilary (1985). Philosophical Papers: Volume 3, Realism and Reason. Cambridge University Press. p. 263. ISBN 978-0-521-31394-0.
- Kuhn, H. W.; Tucker, A. W. (1958). "John von Neumann's work in the theory of games and mathematical economics". Bull. Amer. Math. Soc. 64 (Part 2) (3): 100–122. CiteSeerX 10.1.1.320.2987. doi:10.1090/s0002-9904-1958-10209-8. MR 0096572.
- von Neumann, J: (1928). "Zur Theorie der Gesellschaftsspiele". Mathematische Annalen (in German). 100 (1928): 295–320. Bibcode:1928MatAn.100...32C. doi:10.1007/bf01448847.CS1 maint: Unrecognized language (link)
- .
- For this problem to have a unique solution, it suffices that the nonnegative matrices A and B satisfy an irreducibility condition, generalizing that of the Perron–Frobenius theorem of nonnegative matrices, which considers the (simplified) eigenvalue problem
- A − λ I q = 0,
- where the nonnegative matrix A must be square and where the diagonal matrix I is the identity matrix. Von Neumann's irreducibility condition was called the "whales and wranglers" hypothesis by David Champernowne, who provided a verbal and economic commentary on the English translation of von Neumann's article. Von Neumann's hypothesis implied that every economic process used a positive amount of every economic good. Weaker "irreducibility" conditions were given by David Gale and by John Kemeny, Oskar Morgenstern, and Gerald L. Thompson in the 1950s and then by Stephen M. Robinson in the 1970s.
- pp. xviii, 277.
- pp. i, 74.
- pp. 351–378.
- pp. 277–299.
- Bruckmann, Gerhart; Weber, Wilhelm, eds. (September 21, 1971). Contributions to von Neumann's Growth Model. Proceedings of a Conference Organized by the Institute for Advanced Studies Vienna, Austria, July 6 and 7, 1970. Springer–Verlag. doi:10.1007/978-3-662-24667-2. ISBN 978-3-662-22738-1.
- pp. 250–253.
- Dantzig, George; Thapa, Mukund N. (2003). Linear Programming : 2: Theory and Extensions. New York, NY: Springer-Verlag. ISBN 978-1-4419-3140-5.
- von Neumann, John (1941). "Distribution of the ratio of the mean square successive difference to the variance". Annals of Mathematical Statistics. 12 (4): 367–395. doi:10.1214/aoms/1177731677. JSTOR 2235951.
- Durbin, J.; Watson, G. S. (1950). "Testing for Serial Correlation in Least Squares Regression, I". Biometrika. 37 (3–4): 409–428. doi:10.2307/2332391. JSTOR 2332391. PMID 14801065.
- Sargan, J.D.; Bhargava, Alok (1983). "Testing residuals from least squares regression for being generated by the Gaussian random walk". Econometrica. 51 (1): 153–174. doi:10.2307/1912252. JSTOR 1912252.
- pp. 219–237.
- pp. 205–218.
- Ballistics: Theory and Design of Guns and Ammunition, Second Edition By Donald E. Carlucci, Sidney S. Jacobson, (CRC Press, 26 Aug 2013), page 523
- von Neumann, J.; Richtmyer, R. D. (March 1950). "A Method for the Numerical Calculation of Hydrodynamic Shocks". Journal of Applied Physics. 21 (3): 232–237. Bibcode:1950JAP....21..232V. doi:10.1063/1.1699639.
- Metropolis, Nicholas, ed. (2014). A History of Computing in the Twentieth Century. Elsevier. p. 24. ISBN 978-1-4832-9668-5.
- p. 96.
- p. 77.
- "Von Neumann: The Mathematician". MacTutor History of Mathematics Archive. Retrieved December 16, 2016.
- "Von Neumann: The Mathematician, Part 2". MacTutor History of Mathematics Archive. Retrieved December 16, 2016.
- pp. 180–196.
- pp. 130–133, 157–159.
- pp. 239–245.
- p. 295.
- Sublette, Carey. "Section 8.0 The First Nuclear Weapons". Nuclear Weapons Frequently Asked Questions. Retrieved January 8, 2016.
- pp. 320–327.
- p. 209.
- p. 184.
- pp. 242–245.
- pp. 268–276.
- pp. 371–372.
- p. 205.
- p. 245.
- pp. 171, 374.
- Bernstein, Jeremy (2010). "John von Neumann and Klaus Fuchs: an Unlikely Collaboration". Physics in Perspective. 12 (1): 36–50. Bibcode:2010PhP....12...36B. doi:10.1007/s00016-009-0001-1.
- p. 208.
- pp. 350–351.
- "Weapons' Values to be Appraised". Spokane Daily Chronicle. December 15, 1948. Retrieved January 8, 2015.
- p. 276.
- pp. 367–369.
- pp. 359–365.
- pp. 362–363.
- pp. 258–260.
- pp. 362–364.
- p. 96.
- pp. 167–178.
- p. 159.
- Knuth, Donald E. (1987). "Von Neumann's First Computer Program". In Aspray, W.; Burks, A. Papers of John von Neumann on computing and computer theory. Cambridge: MIT Press. pp. 89–95. ISBN 978-0-262-22030-9.
- pp. 183–184.
- pp. 334–335.
- von Neumann, John (1951). "Various techniques used in connection with random digits". National Bureau of Standards Applied Math Series. 12: 36.
- Von Neumann, John (1951). "Various techniques used in connection with random digits" (PDF). National Bureau of Standards Applied Mathematics Series. 12: 36–38.
- "John W. Mauchly and the Development of the ENIAC Computer". University of Pennsylvania. Retrieved January 27, 2017.
- pp. 279–283.
- "BRL's Scientific Advisory Committee, 1940". U.S. Army Research Laboratory. Retrieved 2018-01-12.
- Knuth, Donald E. (1996). Selected papers on computer science (Center for the Study of Language and Information – Lecture Notes). Stanford, Calif. Cambridge, Mass.: CSLI Publications Cambridge University Press. ISBN 978-1-881526-91-9.
- Rédei, Miklós (ed.). "Letter to R. S. Burlington.". John Von Neumann: Selected Letters. The American Mathematics Society and The London Mathematical Society. pp. 73 ff. ISBN 978-0-8218-9126-1.
- pp. 267–268, 287.
- von Neumann, John (1995). "Probabilistic logics and the synthesis of reliable organisms from unreliable components". In Bródy, F.; Vámos, Tibor. The Neumann Compendium. World Scientific. pp. 567–616. ISBN 978-981-02-2201-7.
- Petrovic, R.; Siljak, D. (1962). "Multiplication by means of coincidence". ACTES Proc. of 3rd Int. Analog Comp. Meeting.
- Afuso, C. (1964). "Quart. Tech. Prog. Rept". Department of Computer Science, University of Illinois at Urbana-Champaign, Illinois.
- pp. 25–27.
- von Neumann, John (1966). A. Burks, ed. The Theory of Self-reproducing Automata. Urbana, IL: Univ. of Illinois Press. ISBN 978-0-598-37798-2.
- "2.1 Von Neumann's Contributions". Molecularassembler.com. Retrieved 2009-09-16.
- "2.1.3 The Cellular Automaton (CA) Model of Machine Replication". Molecularassembler.com. Retrieved 2009-09-16.
- von Neumann, John (1966). Arthur W. Burks, ed. Theory of Self-Reproducing Automata (PDF) (PDF). Urbana and London: University of Illinois Press. ISBN 978-0-598-37798-2.
- 第 8 页
- 第 876 页
- McMullin, B. (2000), "John von Neumann and the Evolutionary Growth of Complexity: Looking Backwards, Looking Forwards...", Artificial Life, 6 (4): 347–361, doi:10.1162/106454600300103674, PMID 11348586
- Toward a Practice of Autonomous Systems: Proceedings of the First European Conference on Artificial Life, Francisco J. Varela, Paul Bourgine, (MIT Press 1992), page 236
- Wolfram, Stephen (2002). A New Kind of Science. Wolfram Media, Inc. p. 1179. ISBN 978-1-57955-008-0.
- Freitas, Robert A., Jr. (1980). "A Self-Reproducing Interstellar Probe". Journal of the British Interplanetary Society. 33: 251–264. Bibcode:1980JBIS...33..251F. Retrieved January 9, 2015.
- pp. 19–38.
- Weather Architecture By Jonathan Hill (Routledge, 2013), page 216
- Charney, J. G.; Fjörtoft, R.; Neumann, J. (1950). "Numerical Integration of the Barotropic Vorticity Equation". Tellus. 2 (4): 237–254. Bibcode:1950TellA...2..237C. doi:10.1111/j.2153-3490.1950.tb00336.x.
- Gilchrist, Bruce, "Remembering Some Early Computers, 1948-1960" (PDF). Archived from the original on December 12, 2006. Retrieved 2006-12-12.CS1 maint: BOT: original-url status unknown (link), Columbia University EPIC, 2006, pp.7-9. (archived 2006) Contains some autobiographical material on Gilchrist's use of the IAS computer beginning in 1952.
- Intraseasonal Variability in the Atmosphere-Ocean Climate System, By William K.-M. Lau, Duane E. Waliser (Springer 2011), page V
- p. 332.
- pp. 236–247.
- p. 16.
- Engineering: Its Role and Function in Human Society edited by William H. Davenport, Daniel I. Rosenthal (Elsevier 2016), page 266
- The Technological Singularity by Murray Shanahan, (MIT Press, 2015), page 233
- Chalmers, David (2010). "The singularity: a philosophical analysis". Journal of Consciousness Studies. 17 (9–10): 7–65.
- pp. 171.
- Poundstone, William, Prisoner's Dilemma, New York: Doubleday 1992
- p. backcover.
- p. 129.
- Teller, Edward (April 1957). "John von Neumann". Bulletin of the Atomic Scientists. 13 (4): 150–151.
- Nowak, Amram (1 January 1966). "John Von Neumann a documentary" (in English). Mathematical Association of America, Committee on Educational Media. OCLC 177660043.CS1 maint: Unrecognized language (link), DVD version (2013) OCLC 897933992.
- .
- p. 258.
- p. 433.
- p. 157.
- The Recollections of Eugene P. Wigner, by Eugene Paul Wigner, Andrew Szanton, Springer, 2013, page 106
- Fermi Remembered, James W. Cronin, University of Chicago Press (2004), page 236
- "Fly Puzzle (Two Trains Puzzle)". Mathworld.wolfram.com. February 15, 2014. Retrieved February 25, 2014.
- "John von Neumann – A Documentary". The Mathematical Association of American. 1966. pp. 16m46s–19m04s. Retrieved 22 February 2016.
- John von Neumann: Life, Work, and Legacy Institute of Advanced Study, Princeton
- p. 7.
- p. vii.
- p. 7.
- p. xiii.
- While there is a general agreement that the initially discovered bone tumour was a secondary growth, sources differ as to the location of the primary cancer. While Macrae gives it as pancreatic, the Life magazine article says it was prostate.
- Read, Colin (2012). The Portfolio Theorists: von Neumann, Savage, Arrow and Markowitz. Great Minds in Finance. Palgrave Macmillan. p. 65. ISBN 978-0230274143. Retrieved September 29, 2017. When von Neumann realised he was incurably ill his logic forced him to realise that he would cease to exist... [a] fate which appeared to him unavoidable but unacceptable.
- "
- 第 124 页 "He was brought up in a Hungary in which anti-Semitism was commonplace, but the family were not overly religious, and for most of his adult years von Neumann held agnostic beliefs."
- 第 170 页 "On the other hand, von Neumann, giving in to Pascal's wager on his death bed, received extreme unction."
- 第 109 页 "He had been completely agnostic for as long as I had known him. As far as I could see this act did not agree with the attitudes and thoughts he had harbored for nearly all his life."
- p. 194.
- p. 380.
- "John von Neumann Theory Prize". Institute for Operations Research and the Management Sciences. Archived from the original on May 13, 2016. Retrieved May 17, 2016.
- "IEEE John von Neumann Medal". Institute of Electrical and Electronics Engineers. Retrieved May 17, 2016.
- "The John von Neumann Lecture". Society for Industrial and Applied Mathematics. Retrieved May 17, 2016.
- "Von Neumann". United States Geological Survey. Retrieved May 17, 2016.
- "22824 von Neumann (1999 RP38)". Jet Propulsion Laboratory. Retrieved February 13, 2018.
- "(22824) von Neumann = 1999 RP38 = 1998 HR2". Minor Planet Center. Retrieved February 13, 2018.
- Anderson, Christopher (November 27, 1989). "NSF Supercomputer Program Looks Beyond Princeton Recall". The Scientist Magazine. Retrieved May 17, 2016.
- "Introducing the John von Neumann Computer Society". John von Neumann Computer Society. Archived from the original on April 29, 2008. Retrieved May 20, 2008.
- p. 321.
- "American Scientists Issue". Smithsonian National Postal Museum. Retrieved May 17, 2016.
- "John von Neumann Award". díjaink – Rajk. Retrieved May 17, 2016.
- John von Neumann University
- John von Neumann 在数学谱系计画的资料。. Retrieved March 17, 2015.
- While Israel Halperin's thesis advisor is often listed as Salomon Bochner, this may be because "Professors at the university direct doctoral theses but those at the Institute do not. Unaware of this, in 1934 I asked von Neumann if he would direct my doctoral thesis. He replied Yes." (Halperin, Israel (1990). The Extraordinary Inspiration of John von Neumann. Proceedings of Symposia in Pure Mathematics. 50. pp. 15–17. doi:10.1090/pspum/050/1067747. ISBN 978-0-8218-1487-1.)
12. 参考文献
[1] ^Rèdei 1999, p. 3..
[2] ^Doran et al. 2004, p. 8..
[3] ^Doran et al. 2004, p. 1..
[4] ^Myhrvold, Nathan (March 21, 1999). "John von Neumann". Time..
[5] ^Dyson 1998, p. xxi..
[6] ^Macrae 1992, pp. 38–42..
[7] ^Macrae 1992, pp. 37–38..
[8] ^Macrae 1992, p. 39..
[9] ^Macrae 1992, pp. 44–45..
[10] ^Henderson 2007, p. 30..
[11] ^Schneider, Gersting & Brinkman 2015, p. 28..
[12] ^Mitchell 2009, p. 124..
[13] ^Macrae 1992, pp. 46–47..
[14] ^Macrae 1992, p. 52..
[15] ^Macrae 1992, pp. 70–71..
[16] ^Doran et al. 2004, p. 3..
[17] ^Macrae 1992, pp. 32–33..
[18] ^Nasar 2001, p. 81..
[19] ^Macrae 1992, p. 84..
[20] ^von Kármán, T., & Edson, L. (1967). The wind and beyond. Little, Brown & Company..
[21] ^Macrae 1992, pp. 85–87..
[22] ^Macrae 1992, p. 97..
[23] ^von Neumann, J. (1928). "Die Axiomatisierung der Mengenlehre". Mathematische Zeitschrift (in German). 27 (1): 669–752. doi:10.1007/BF01171122. ISSN 0025-5874.CS1 maint: Unrecognized language (link).
[24] ^Macrae 1992, pp. 86–87..
[25] ^The Collected Works of Eugene Paul Wigner: Historical, Philosophical, and Socio-Political Papers. Historical and Biographical Reflections and Syntheses, By Eugene Paul Wigner, (Springer 2013), page 128.
[26] ^Macrae 1992, pp. 98–99..
[27] ^Hashagen, Ulf (2010). "Die Habilitation von John von Neumann an der Friedrich-Wilhelms-Universität in Berlin: Urteile über einen ungarisch-jüdischen Mathematiker in Deutschland im Jahr 1927". Historia Mathematica. 37 (2): 242–280. doi:10.1016/j.hm.2009.04.002..
[28] ^The History Of Game Theory, Volume 1: From the Beginnings to 1945, By Mary-Ann Dimand, Robert W Dimand, (Routledge, 2002), page 129.
[29] ^Macrae 1992, p. 145..
[30] ^Macrae 1992, pp. 143–144..
[31] ^Macrae 1992, pp. 155–157..
[32] ^"Marina Whitman". The Gerald R. Ford School of Public Policy at the University of Michigan. 2014-07-18. Retrieved January 5, 2015..
[33] ^Macrae 1992, pp. 170–174..
[34] ^Bochner, S. (1958). "John von Neumann; A Biographical Memoir" (PDF). National Academy of Sciences. Retrieved August 16, 2015..
[35] ^Macrae 1992, pp. 43, 157..
[36] ^Macrae 1992, pp. 167–168..
[37] ^Macrae 1992, p. 371..
[38] ^Macrae 1992, pp. 195–196..
[39] ^Macrae 1992, pp. 57–58..
[40] ^Ulam 1983, p. 70..
[41] ^Macrae 1992, pp. 170–171..
[42] ^Regis 1987, p. 103..
[43] ^"Conversation with Marina Whitman". Gray Watson (256.com). Archived from the original on April 28, 2011. Retrieved January 30, 2011..
[44] ^Poundstone, William (May 4, 2012). "Unleashing the Power". The New York Times..
[45] ^Blair, pp. 89–104..
[46] ^Macrae 1992, p. 150..
[47] ^Macrae 1992, p. 48..
[48] ^Blair 1957, p. 94..
[49] ^Stern, Nancy (January 20, 1981). "An Interview with Cuthbert C. Hurd" (PDF). Charles Babbage Institute, University of Minnesota. Retrieved June 3, 2010..
[50] ^Rota 1989, pp. 26–27..
[51] ^Macrae 1992, p. 75..
[52] ^Van Heijenoort 1967, pp. 393–394..
[53] ^Macrae 1992, pp. 104–105..
[54] ^von Neumann 2005, p. 123..
[55] ^Dawson 1997, p. 70..
[56] ^von Neumann 2005, p. 124..
[57] ^Macrae 1992, p. 182..
[58] ^von Neumann, J. (1929), "Zur allgemeinen Theorie des Masses" (PDF), Fundamenta Mathematicae, 13: 73–116, doi:10.4064/fm-13-1-73-116.
[59] ^Two famous papers are: von Neumann, John (1932). "Proof of the Quasi-ergodic Hypothesis". Proc Natl Acad Sci USA. 18 (1): 70–82. Bibcode:1932PNAS...18...70N. doi:10.1073/pnas.18.1.70. PMC 1076162. PMID 16577432.. von Neumann, John (1932). "Physical Applications of the Ergodic Hypothesis". Proc Natl Acad Sci USA. 18 (3): 263–266. Bibcode:1932PNAS...18..263N. doi:10.1073/pnas.18.3.263. JSTOR 86260. PMC 1076204. PMID 16587674.. Hopf, Eberhard (1939). "Statistik der geodätischen Linien in Mannigfaltigkeiten negativer Krümmung". Leipzig Ber. Verhandl. Sächs. Akad. Wiss. 91: 261–304..
[60] ^Halmos, Paul R. (1958). "Von Neumann on measure and ergodic theory" (PDF). Bull. Amer. Math. Soc. 64 (3, Part 2): 86–94. doi:10.1090/S0002-9904-1958-10203-7..
[61] ^Petz & Redi 1995, pp. 163–181..
[62] ^"Von Neumann Algebras" (PDF). Princeton University. Retrieved January 6, 2016..
[63] ^"Direct Integrals of Hilbert Spaces and von Neumann Algebras" (PDF). University of California at Los Angeles. Archived from the original (PDF) on 2015-07-02. Retrieved January 6, 2016..
[64] ^Van Hove, Léon (1958). "Von Neumann's Contributions to Quantum Theory". Bulletin of the American Mathematical Society. 64 (3): 95–99. doi:10.1090/s0002-9904-1958-10206-2..
[65] ^von Neumann, J. (1933). "Die Einfuhrung Analytischer Parameter in Topologischen Gruppen". Annals of Mathematics. 2. 34 (1): 170–179. doi:10.2307/1968347. JSTOR 1968347..
[66] ^"AMS Bôcher Prize". AMS. January 5, 2016. Retrieved 2018-01-12..
[67] ^*Neumann, John von (1936b), "Examples of continuous geometries", Proc. Natl. Acad. Sci. USA, 22 (2): 101–108, Bibcode:1936PNAS...22..101N, doi:10.1073/pnas.22.2.101, JFM 62.0648.03, JSTOR 86391, PMC 1076713, PMID 16588050 Neumann, John von (1998) [1960], Continuous geometry, Princeton Landmarks in Mathematics, Princeton University Press, ISBN 978-0-691-05893-1, MR 0120174 Neumann, John von (1962), Taub, A. H., ed., Collected works. Vol. IV: Continuous geometry and other topics, Oxford: Pergamon Press, MR 0157874 Neumann, John von (1981) [1937], Halperin, Israel, ed., "Continuous geometries with a transition probability", Memoirs of the American Mathematical Society, 34 (252), doi:10.1090/memo/0252, ISBN 978-0-8218-2252-4, ISSN 0065-9266, MR 0634656.
[68] ^Macrae 1992, p. 140..
[69] ^von Neumann, John (1930). "Zur Algebra der Funktionaloperationen und Theorie der normalen Operatoren". Mathematische Annalen (in German). 102 (1): 370–427. Bibcode:1930MatAn.102..685E. doi:10.1007/BF01782352.CS1 maint: Unrecognized language (link). The original paper on von Neumann algebras..
[70] ^Birkhoff, Garrett (1958). Von Neumann and lattice theory (PDF). Bulletin of the American Mathematical Society. 64. pp. 50–56. doi:10.1090/S0002-9904-1958-10192-5. ISBN 978-0-8218-1025-5..
[71] ^Macrae 1992, pp. 139–141..
[72] ^Macrae 1992, p. 142..
[73] ^Hermann, Grete (1935). "Die naturphilosophischen Grundlagen der Quantenmechanik". Naturwissenschaften. 23 (42): 718–721. Bibcode:1935NW.....23..718H. doi:10.1007/BF01491142. English translation in Hermann, Grete (2016). Crull, Elise; Bacciagaluppi, Guido, eds. Grete Hermann — Between physics and philosophy. Springer. pp. 239–278..
[74] ^Bell, John S. (1966). "On the problem of hidden variables in quantum mechanics". Reviews of Modern Physics. 38 (3): 447–452. Bibcode:1966RvMP...38..447B. doi:10.1103/RevModPhys.38.447..
[75] ^Bub, Jeffrey (2010). "Von Neumann's 'No Hidden Variables' Proof: A Re-Appraisal". Foundations of Physics. 40 (9–10): 1333–1340. arXiv:1006.0499. Bibcode:2010FoPh...40.1333B. doi:10.1007/s10701-010-9480-9..
[76] ^Mermin, N. David; Schack, Rüdiger (2018). "Homer nodded: von Neumann's surprising oversight". Foundations of Physics. 48 (9): 1007–1020. arXiv:1805.10311. Bibcode:2018FoPh...48.1007M. doi:10.1007/s10701-018-0197-5..
[77] ^Freire, Olival Jr. (2006). "Philosophy enters the optics laboratory: Bell's theorem and its first experimental tests (1965–1982)". Studies in History and Philosophy of Modern Physics. 37 (4): 577–616. arXiv:physics/0508180. Bibcode:2006SHPMP..37..577F. doi:10.1016/j.shpsb.2005.12.003..
[78] ^Wigner, Eugene; Henry Margenau (December 1967). "Remarks on the Mind Body Question, in Symmetries and Reflections, Scientific Essays". American Journal of Physics. 35 (12): 1169–1170. Bibcode:1967AmJPh..35.1169W. doi:10.1119/1.1973829..
[79] ^Schlosshauer, M.; Koer, J.; Zeilinger, A. (2013). "A Snapshot of Foundational Attitudes Toward Quantum Mechanics". Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics. 44 (3): 222–230. arXiv:1301.1069. Bibcode:2013SHPMP..44..222S. doi:10.1016/j.shpsb.2013.04.004..
[80] ^Quantum Information Theory, By Mark M. Wilde, (Cambridge University Press 2013), page 252.
[81] ^von Neumann, John (1927), "Wahrscheinlichkeitstheoretischer Aufbau der Quantenmechanik", Göttinger Nachrichten, 1: 245–272.
[82] ^Schlüter, Michael and Lu Jeu Sham (1982), "Density functional theory", Physics Today, 35 (2): 36–43, Bibcode:1982PhT....35b..36S, doi:10.1063/1.2914933.
[83] ^Ugo Fano (June 1995), "Density matrices as polarization vectors", Rendiconti Lincei, 6 (2): 123–130, doi:10.1007/BF03001661.
[84] ^Dualism, Platonism and Voluntarism: Explorations at the Quantum, Microscopic, Mesoscopic and Symbolic Neural Levels, (Cambridge Scholars 2016), page 215.
[85] ^Gabbay, Dov M.; Woods, John (2007). "The History of Quantum Logic". The Many Valued and Nonmonotonic Turn in Logic. Elsevier. pp. 205–2017. ISBN 978-0-08-054939-2..
[86] ^Birkhoff, Garrett; von Neumann, John (October 1936). "The Logic of Quantum Mechanics". Annals of Mathematics. 37 (4): 823–843. doi:10.2307/1968621. JSTOR 1968621..
[87] ^Putnam, Hilary (1985). Philosophical Papers: Volume 3, Realism and Reason. Cambridge University Press. p. 263. ISBN 978-0-521-31394-0..
[88] ^Kuhn, H. W.; Tucker, A. W. (1958). "John von Neumann's work in the theory of games and mathematical economics". Bull. Amer. Math. Soc. 64 (Part 2) (3): 100–122. CiteSeerX 10.1.1.320.2987. doi:10.1090/s0002-9904-1958-10209-8. MR 0096572..
[89] ^von Neumann, J: (1928). "Zur Theorie der Gesellschaftsspiele". Mathematische Annalen (in German). 100 (1928): 295–320. Bibcode:1928MatAn.100...32C. doi:10.1007/bf01448847.CS1 maint: Unrecognized language (link).
[90] ^Blume 2008..
[91] ^For this problem to have a unique solution, it suffices that the nonnegative matrices A and B satisfy an irreducibility condition, generalizing that of the Perron–Frobenius theorem of nonnegative matrices, which considers the (simplified) eigenvalue problem A − λ I q = 0, where the nonnegative matrix A must be square and where the diagonal matrix I is the identity matrix. Von Neumann's irreducibility condition was called the "whales and wranglers" hypothesis by David Champernowne, who provided a verbal and economic commentary on the English translation of von Neumann's article. Von Neumann's hypothesis implied that every economic process used a positive amount of every economic good. Weaker "irreducibility" conditions were given by David Gale and by John Kemeny, Oskar Morgenstern, and Gerald L. Thompson in the 1950s and then by Stephen M. Robinson in the 1970s..
[92] ^Morgenstern & Thompson 1976, pp. xviii, 277..
[93] ^Rockafellar 1970, pp. i, 74..
[94] ^Rockafellar 1974, pp. 351–378..
[95] ^Ye 1997, pp. 277–299..
[96] ^Bruckmann, Gerhart; Weber, Wilhelm, eds. (September 21, 1971). Contributions to von Neumann's Growth Model. Proceedings of a Conference Organized by the Institute for Advanced Studies Vienna, Austria, July 6 and 7, 1970. Springer–Verlag. doi:10.1007/978-3-662-24667-2. ISBN 978-3-662-22738-1..
[97] ^Macrae 1992, pp. 250–253..
[98] ^Dantzig, George; Thapa, Mukund N. (2003). Linear Programming : 2: Theory and Extensions. New York, NY: Springer-Verlag. ISBN 978-1-4419-3140-5..
[99] ^von Neumann, John (1941). "Distribution of the ratio of the mean square successive difference to the variance". Annals of Mathematical Statistics. 12 (4): 367–395. doi:10.1214/aoms/1177731677. JSTOR 2235951..
[100] ^Durbin, J.; Watson, G. S. (1950). "Testing for Serial Correlation in Least Squares Regression, I". Biometrika. 37 (3–4): 409–428. doi:10.2307/2332391. JSTOR 2332391. PMID 14801065..
[101] ^Sargan, J.D.; Bhargava, Alok (1983). "Testing residuals from least squares regression for being generated by the Gaussian random walk". Econometrica. 51 (1): 153–174. doi:10.2307/1912252. JSTOR 1912252..
[102] ^von Neumann 1963a, pp. 219–237..
[103] ^von Neumann 1963b, pp. 205–218..
[104] ^Ballistics: Theory and Design of Guns and Ammunition, Second Edition By Donald E. Carlucci, Sidney S. Jacobson, (CRC Press, 26 Aug 2013), page 523.
[105] ^von Neumann, J.; Richtmyer, R. D. (March 1950). "A Method for the Numerical Calculation of Hydrodynamic Shocks". Journal of Applied Physics. 21 (3): 232–237. Bibcode:1950JAP....21..232V. doi:10.1063/1.1699639..
[106] ^Metropolis, Nicholas, ed. (2014). A History of Computing in the Twentieth Century. Elsevier. p. 24. ISBN 978-1-4832-9668-5..
[107] ^Ulam 1983, p. 96..
[108] ^Dyson 1998, p. 77..
[109] ^"Von Neumann: The Mathematician". MacTutor History of Mathematics Archive. Retrieved December 16, 2016..
[110] ^"Von Neumann: The Mathematician, Part 2". MacTutor History of Mathematics Archive. Retrieved December 16, 2016..
[111] ^von Neumann 1947, pp. 180–196..
[112] ^Regis, Ed (November 8, 1992). "Johnny Jiggles the Planet". The New York Times. Retrieved February 4, 2008..
[113] ^Hoddeson et al. 1993, pp. 239–245..
[114] ^Hoddeson et al. 1993, p. 295..
[115] ^Sublette, Carey. "Section 8.0 The First Nuclear Weapons". Nuclear Weapons Frequently Asked Questions. Retrieved January 8, 2016..
[116] ^Hoddeson et al. 1993, pp. 320–327..
[117] ^Macrae 1992, p. 209..
[118] ^Hoddeson et al. 1993, p. 184..
[119] ^Macrae 1992, pp. 242–245..
[120] ^Groves 1962, pp. 268–276..
[121] ^Hoddeson et al. 1993, pp. 371–372..
[122] ^Macrae 1992, p. 205..
[123] ^Macrae 1992, p. 245..
[124] ^Herken 2002, pp. 171, 374..
[125] ^Bernstein, Jeremy (2010). "John von Neumann and Klaus Fuchs: an Unlikely Collaboration". Physics in Perspective. 12 (1): 36–50. Bibcode:2010PhP....12...36B. doi:10.1007/s00016-009-0001-1..
[126] ^Macrae 1992, p. 208..
[127] ^Macrae 1992, pp. 350–351..
[128] ^"Weapons' Values to be Appraised". Spokane Daily Chronicle. December 15, 1948. Retrieved January 8, 2015..
[129] ^Heims 1980, p. 276..
[130] ^Macrae 1992, pp. 367–369..
[131] ^Macrae 1992, pp. 359–365..
[132] ^Macrae 1992, pp. 362–363..
[133] ^Heims 1980, pp. 258–260..
[134] ^Macrae 1992, pp. 362–364..
[135] ^Blair 1957, p. 96..
[136] ^Goldstine 1980, pp. 167–178..
[137] ^Knuth 1998, p. 159..
[138] ^Knuth, Donald E. (1987). "Von Neumann's First Computer Program". In Aspray, W.; Burks, A. Papers of John von Neumann on computing and computer theory. Cambridge: MIT Press. pp. 89–95. ISBN 978-0-262-22030-9..
[139] ^Macrae 1992, pp. 183–184..
[140] ^Macrae 1992, pp. 334–335..
[141] ^von Neumann, John (1951). "Various techniques used in connection with random digits". National Bureau of Standards Applied Math Series. 12: 36..
[142] ^Von Neumann, John (1951). "Various techniques used in connection with random digits" (PDF). National Bureau of Standards Applied Mathematics Series. 12: 36–38..
[143] ^"John W. Mauchly and the Development of the ENIAC Computer". University of Pennsylvania. Retrieved January 27, 2017..
[144] ^Macrae 1992, pp. 279–283..
[145] ^"BRL's Scientific Advisory Committee, 1940". U.S. Army Research Laboratory. Retrieved 2018-01-12..
[146] ^Knuth, Donald E. (1996). Selected papers on computer science (Center for the Study of Language and Information – Lecture Notes). Stanford, Calif. Cambridge, Mass.: CSLI Publications Cambridge University Press. ISBN 978-1-881526-91-9..
[147] ^Rédei, Miklós (ed.). "Letter to R. S. Burlington.". John Von Neumann: Selected Letters. The American Mathematics Society and The London Mathematical Society. pp. 73 ff. ISBN 978-0-8218-9126-1..
[148] ^Dyson 2012, pp. 267–268, 287..
[149] ^von Neumann, John (1995). "Probabilistic logics and the synthesis of reliable organisms from unreliable components". In Bródy, F.; Vámos, Tibor. The Neumann Compendium. World Scientific. pp. 567–616. ISBN 978-981-02-2201-7..
[150] ^Petrovic, R.; Siljak, D. (1962). "Multiplication by means of coincidence". ACTES Proc. of 3rd Int. Analog Comp. Meeting..
[151] ^Afuso, C. (1964). "Quart. Tech. Prog. Rept". Department of Computer Science, University of Illinois at Urbana-Champaign, Illinois..
[152] ^Rocha (2015),pp. 25–27..
[153] ^von Neumann, John (1966). A. Burks, ed. The Theory of Self-reproducing Automata. Urbana, IL: Univ. of Illinois Press. ISBN 978-0-598-37798-2..
[154] ^"2.1 Von Neumann's Contributions". Molecularassembler.com. Retrieved 2009-09-16..
[155] ^"2.1.3 The Cellular Automaton (CA) Model of Machine Replication". Molecularassembler.com. Retrieved 2009-09-16..
[156] ^Bialynicki-Birula, Bialynicka-Birula 2004,第 8 页.
[157] ^Wolfram 2002,第 876 页.
[158] ^McMullin, B. (2000), "John von Neumann and the Evolutionary Growth of Complexity: Looking Backwards, Looking Forwards...", Artificial Life, 6 (4): 347–361, doi:10.1162/106454600300103674, PMID 11348586.
[159] ^Toward a Practice of Autonomous Systems: Proceedings of the First European Conference on Artificial Life, Francisco J. Varela, Paul Bourgine, (MIT Press 1992), page 236.
[160] ^Wolfram, Stephen (2002). A New Kind of Science. Wolfram Media, Inc. p. 1179. ISBN 978-1-57955-008-0..
[161] ^Freitas, Robert A., Jr. (1980). "A Self-Reproducing Interstellar Probe". Journal of the British Interplanetary Society. 33: 251–264. Bibcode:1980JBIS...33..251F. Retrieved January 9, 2015..
[162] ^Filiol 2005, pp. 19–38..
[163] ^Weather Architecture By Jonathan Hill (Routledge, 2013), page 216.
[164] ^Charney, J. G.; Fjörtoft, R.; Neumann, J. (1950). "Numerical Integration of the Barotropic Vorticity Equation". Tellus. 2 (4): 237–254. Bibcode:1950TellA...2..237C. doi:10.1111/j.2153-3490.1950.tb00336.x..
[165] ^Gilchrist, Bruce, "Remembering Some Early Computers, 1948-1960" (PDF). Archived from the original on December 12, 2006. Retrieved 2006-12-12.CS1 maint: BOT: original-url status unknown (link), Columbia University EPIC, 2006, pp.7-9. (archived 2006) Contains some autobiographical material on Gilchrist's use of the IAS computer beginning in 1952..
[166] ^Intraseasonal Variability in the Atmosphere-Ocean Climate System, By William K.-M. Lau, Duane E. Waliser (Springer 2011), page V.
[167] ^Macrae 1992, p. 332..
[168] ^Heims 1980, pp. 236–247..
[169] ^Macrae 1992, p. 16..
[170] ^Engineering: Its Role and Function in Human Society edited by William H. Davenport, Daniel I. Rosenthal (Elsevier 2016), page 266.
[171] ^The Technological Singularity by Murray Shanahan, (MIT Press, 2015), page 233.
[172] ^Chalmers, David (2010). "The singularity: a philosophical analysis". Journal of Consciousness Studies. 17 (9–10): 7–65..
[173] ^Goldstine 1980, pp. 171..
[174] ^Poundstone, William, Prisoner's Dilemma, New York: Doubleday 1992.
[175] ^Blair 1957, p. 90..
[176] ^Wigner, Mehra & Wightman 1995, p. 129..
[177] ^Kaplan, Michael and Kaplan, Ellen (2006) Chances are–: adventures in probability. Viking..
[178] ^Nowak, Amram (1 January 1966). "John Von Neumann a documentary" (in English). Mathematical Association of America, Committee on Educational Media. OCLC 177660043.CS1 maint: Unrecognized language (link), DVD version (2013) OCLC 897933992..
[179] ^Glimm, Impagliazzo & Singer 1990..
[180] ^Mirowski 2002, p. 258..
[181] ^Bronowski 1974, p. 433..
[182] ^Petković 2009, p. 157..
[183] ^The Recollections of Eugene P. Wigner, by Eugene Paul Wigner, Andrew Szanton, Springer, 2013, page 106.
[184] ^Fermi Remembered, James W. Cronin, University of Chicago Press (2004), page 236.
[185] ^"Fly Puzzle (Two Trains Puzzle)". Mathworld.wolfram.com. February 15, 2014. Retrieved February 25, 2014..
[186] ^"John von Neumann – A Documentary". The Mathematical Association of American. 1966. pp. 16m46s–19m04s. Retrieved 22 February 2016..
[187] ^John von Neumann: Life, Work, and Legacy Institute of Advanced Study, Princeton.
[188] ^von Neumann 2005, p. 7..
[189] ^Glimm, Impagliazzo & Singer 1990, p. vii..
[190] ^Dieudonné 2008, p. 90..
[191] ^von Neumann 2005, p. xiii..
[192] ^While there is a general agreement that the initially discovered bone tumour was a secondary growth, sources differ as to the location of the primary cancer. While Macrae gives it as pancreatic, the Life magazine article says it was prostate..
[193] ^Read, Colin (2012). The Portfolio Theorists: von Neumann, Savage, Arrow and Markowitz. Great Minds in Finance. Palgrave Macmillan. p. 65. ISBN 978-0230274143. Retrieved September 29, 2017. When von Neumann realised he was incurably ill his logic forced him to realise that he would cease to exist... [a] fate which appeared to him unavoidable but unacceptable..
[194] ^Halmos, P. R. (1973). "The Legend of von Neumann". The American Mathematical Monthly. 80 (4): 382–394. doi:10.2307/2319080. JSTOR 2319080..
[195] ^Dransfield & Dransfield 2003,第 124 页 "He was brought up in a Hungary in which anti-Semitism was commonplace, but the family were not overly religious, and for most of his adult years von Neumann held agnostic beliefs.".
[196] ^Ayoub 2004,第 170 页 "On the other hand, von Neumann, giving in to Pascal's wager on his death bed, received extreme unction.".
[197] ^Pais 2006,第 109 页 "He had been completely agnostic for as long as I had known him. As far as I could see this act did not agree with the attitudes and thoughts he had harbored for nearly all his life.".
[198] ^Poundstone 1993, p. 194..
[199] ^Blair 1957, p. 104..
[200] ^"John von Neumann Theory Prize". Institute for Operations Research and the Management Sciences. Archived from the original on May 13, 2016. Retrieved May 17, 2016..
[201] ^"IEEE John von Neumann Medal". Institute of Electrical and Electronics Engineers. Retrieved May 17, 2016..
[202] ^"The John von Neumann Lecture". Society for Industrial and Applied Mathematics. Retrieved May 17, 2016..
[203] ^"Von Neumann". United States Geological Survey. Retrieved May 17, 2016..
[204] ^"22824 von Neumann (1999 RP38)". Jet Propulsion Laboratory. Retrieved February 13, 2018..
[205] ^"(22824) von Neumann = 1999 RP38 = 1998 HR2". Minor Planet Center. Retrieved February 13, 2018..
[206] ^Anderson, Christopher (November 27, 1989). "NSF Supercomputer Program Looks Beyond Princeton Recall". The Scientist Magazine. Retrieved May 17, 2016..
[207] ^"Introducing the John von Neumann Computer Society". John von Neumann Computer Society. Archived from the original on April 29, 2008. Retrieved May 20, 2008..
[208] ^Kent & Williams 1994, p. 321..
[209] ^"American Scientists Issue". Smithsonian National Postal Museum. Retrieved May 17, 2016..
[210] ^"John von Neumann Award". díjaink – Rajk. Retrieved May 17, 2016..
[211] ^John von Neumann University.
[212] ^von Neumann, John (1966). Arthur W. Burks, ed. Theory of Self-Reproducing Automata (PDF) (PDF). Urbana and London: University of Illinois Press. ISBN 978-0-598-37798-2..
友情链接: 超理论坛 | ©小时科技 保留一切权利