trie 树（字典树）

贡献者：有机物

　　 $Trie$ 树（字典树）高效的存储和查找字符串集合的数据结构。

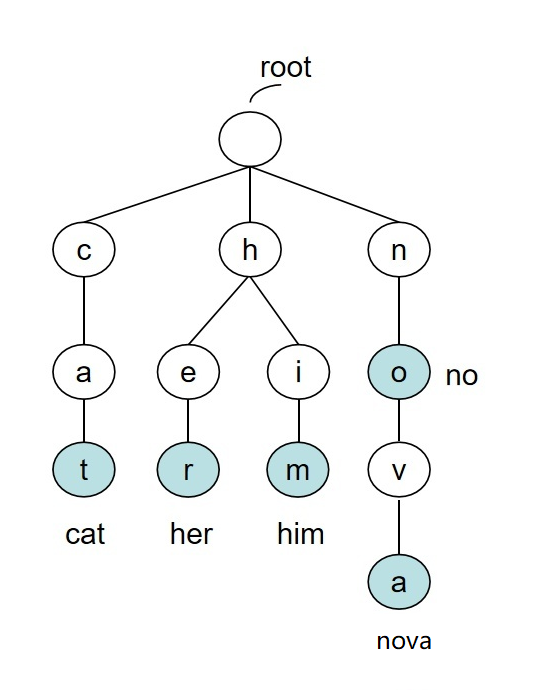
　　假设要存储这些字符串： cat、her、him、no、nova。

　　对应在图上就长这样：

图 1：

trie

树

　　插入字符串：从根结点开始看，看有没有这个字母，有的话就走，没有的话就创建一个新的字母结点。存储每个单词一般都会在这个单词的结尾字母打一个标记（如图中的蓝色结点），意思是以这个字母为结尾的路径是有一个单词的。插入一个字符串动图

　　查找字符串：比如要查找 him 这个单词，我们就从根结点开始走，依次走每个字母，如果找到了要查找的字符串的结尾字母并且这个结点上有标记，就表示找到了这个字符串。查找字符串动图

　　来看一个具体题目：维护一个字符串集合，支持两种操作：

I x 向集合中插入一个字符串 x；
Q x 询问一个字符串在集合中出现了多少次。

　　共有 $N$ 个操作，输入的字符串总长度不超过 $10^{5}$ ，字符串仅包含小写英文字母。

样例：
输入：      输出：
11
I cat       
Q cat       1
Q ca        0
I her
Q her       1
I him
Q him       1
I no 
Q no        1
I nova
Q nova      1

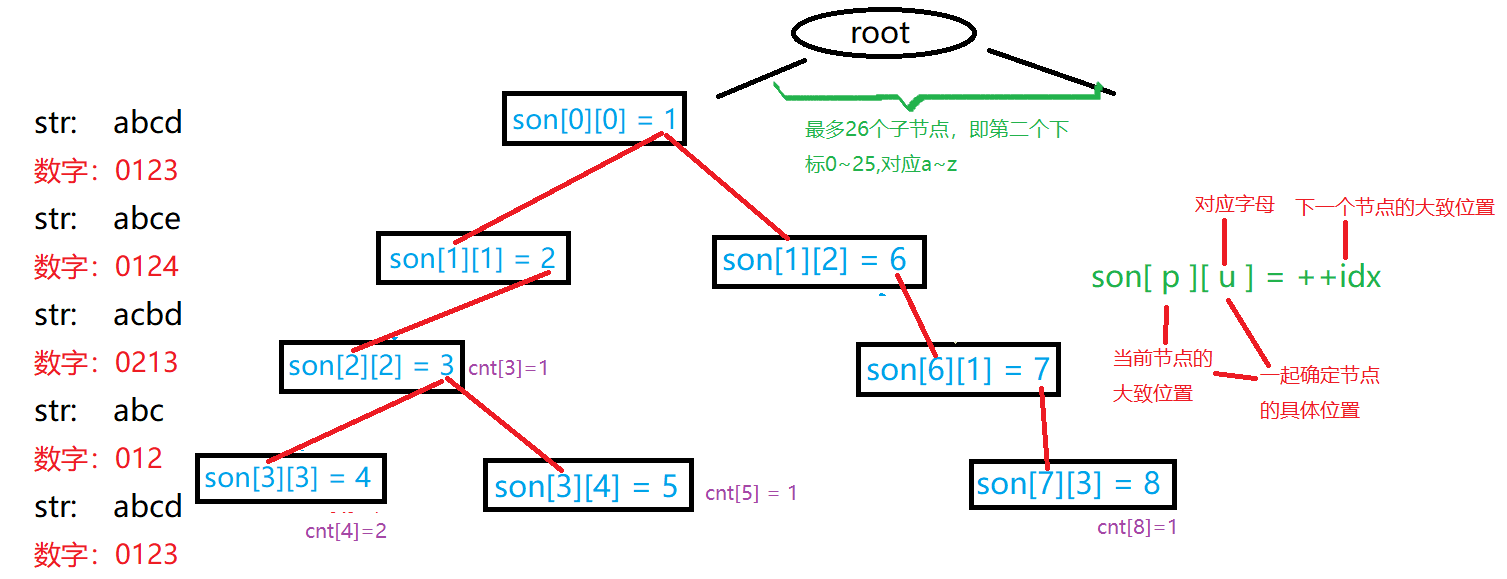
　　开一个数组 sno[N][26] 来表示每个点的所有儿子，第一维存储结点大小，第二维存储每个字母，因为字符串仅包含小写英文字母，所以第二维只开 $26$ 的大小就可以了。cnt[N] 表示以当前字母为结点的字母有多少个（标记）idx 的含义和链表里的 idx 含义一样。

图 2：数组模拟

Trie

树

// 插入（存储）字符串
void insert(string str)
{
    int p = 0;  // 类似指针，从根结点开始
    for (int i = 0; str[i]; i ++ )
    {
        int u = str[i] - 'a';  // 'a' ~ 'z' 映射成 0 ~ 25
        if (!son[p][u]) son[p][u] = ++ idx;  // 该结点不存在，创建结点
        p = son[p][u];     // 使 p 指向（走到）子结点
    }
    
    cnt[p] ++ ;  // 以 p 结点为结尾的单词数量 ++ 
}

// 查询字符串出现的次数
int find(string str)
{
    int p = 0;
    for (int i = 0; str[i]; i ++ )
    {
        int u = str[i] - 'a';
        if (!son[p][u]) return 0; // 没有的话就返回 0，表示这个字符串在集合中没有出现过
        p = son[p][u];            // 有的话走向子结点
    }

    return cnt[p];   // 返回以 p 结点为结尾的单词数量
}

致读者：小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。因此，我们请求广大读者热心打赏 ，使网站得以健康发展。如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损，并在接下来的一年里向所有读者继续免费提供优质内容。但遗憾的是只有不到 1% 的读者愿意捐款，他们的付出帮助了 99% 的读者免费获取知识，我们在此表示感谢。