容斥原理

贡献者： lzq

本文缺少预备知识，初学者可能会遇到困难。

1. 容斥原理

　　容斥原理是组合数学中的一个重要原理，是用于计算多个集合的并集中元素数量时的一种简化计数的方法。

　　首先,我们考虑两个集合的情形。设有两个集合 $A$ 和 $B$，我们要计算这两个集合的并集 $A \cup B$ 的元素数量。如果直接将两个集合的元素数量相加，$ |A| + |B| $，会重复计算 $A$ 和 $B$ 的交集 $A \cap B$ 中的元素。因此，为了得到准确的元素数量，需要减去这个交集的大小，即： $|A \cup B| = |A| + |B| - |A \cap B|$

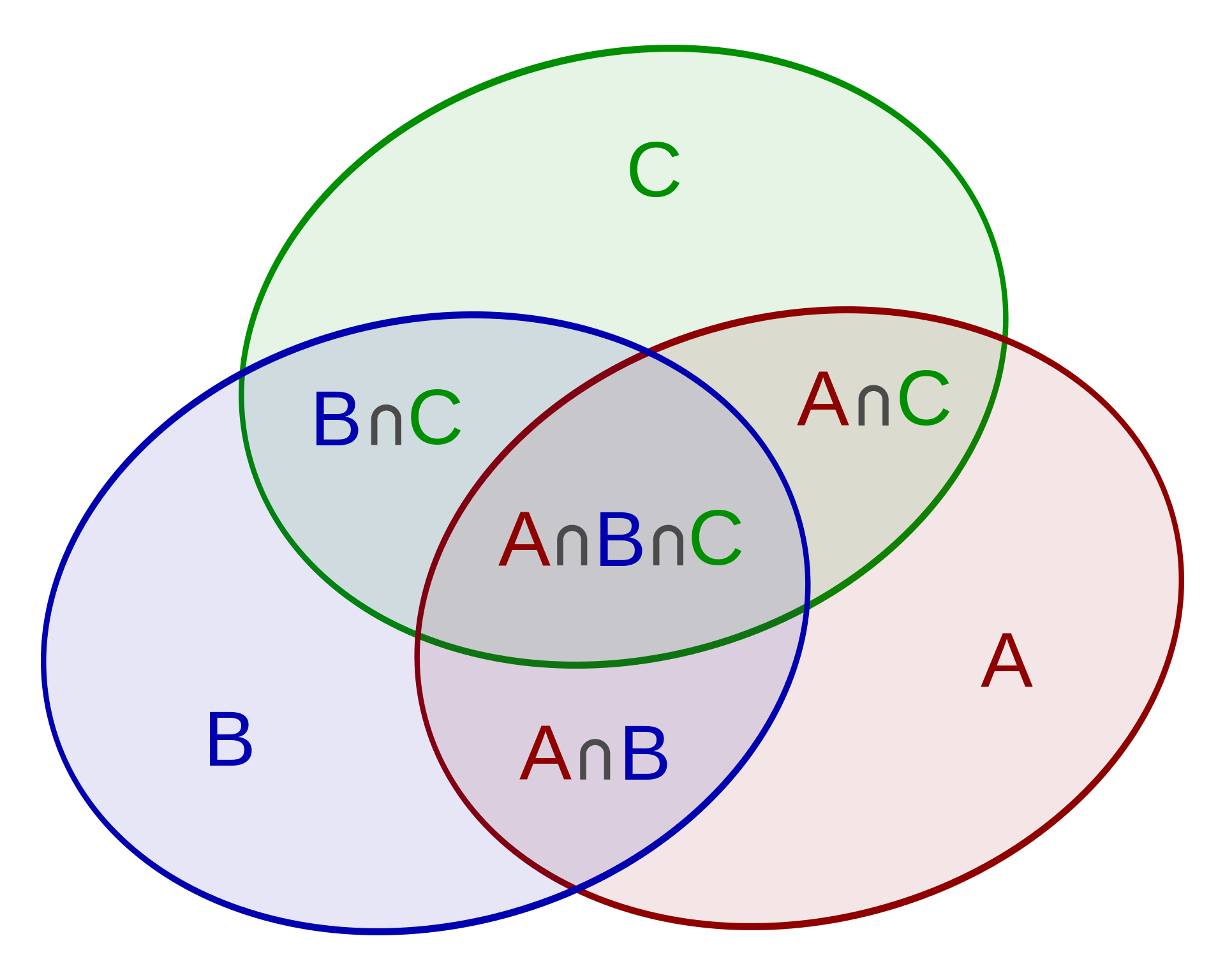
　　当涉及到三个集合 $A$、$B$ 和 $C$ 时，如下图所示，首先直观地将每个集合的大小相加，再减去两两交集的大小，但我们再次重复计算了三个集合共同部分的元素。因此，需要加回一次这个三个集合的交集的大小： $|A \cup B \cup C| = |A| + |B| + |C| - |A \cap B| - |A \cap C| - |B \cap C| + |A \cap B \cap C|$

图 1：三个集合的情况

　　推广到任意 $n$ 个集合的情况：

　　使用 $|S|$ 来表示集合 S 的元素个数, 并把 S 的概率记作 Pr(S). 对于集合 $A_1, A_2, \ldots, A_n$。容斥原理可以用来计算这些集合并集的大小或这个集合所对应的事件的概率概率。

\begin{equation} \left|\bigcup_{i=1}^{n} A_i\right| = \sum_{i=1}^{n} |A_i| - \sum_{1 \leq i < j \leq n} |A_i \cap A_j| + \sum_{1 \leq i < j < k \leq n} |A_i \cap A_j \cap A_k| - \cdots + (-1)^{n-1} |A_1 \cap A_2 \cap \cdots \cap A_n|~. \end{equation}

　　如果将集合的大小 $|S|$ 替换为集合的概率 $\text{Pr}(S)$，则上述公式仍然成立。因此，对于计算概率的情况，公式可以表示为：

\begin{equation} \text{Pr}\left(\bigcup_{i=1}^{n} A_i\right) = \sum_{i=1}^{n} \text{Pr}(A_i) - \sum_{1 \leq i < j \leq n} \text{Pr}(A_i \cap A_j) + \sum_{1 \leq i < j < k \leq n} \text{Pr}(A_i \cap A_j \cap A_k) - \cdots + (-1)^{n-1} \text{Pr}(A_1 \cap A_2 \cap \cdots \cap A_n) ~. \end{equation}

　　这个公式通过交替添加和减去所有可能的交集的大小来准确计数，从而消除了重复计数的问题。每个交集只计算一次，并且根据它涉及的集合数量的奇偶性，决定是加上还是减去这个数值。这样，最终得到的结果就是所有集合的并集的准确大小，从而简化分解了多个集合重叠时的计数问题。（等价于求解 “多个事件中至少有一个发生” 的概率问题）

致读者：小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。因此，我们请求广大读者热心打赏 ，使网站得以健康发展。如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损，并在接下来的一年里向所有读者继续免费提供优质内容。但遗憾的是只有不到 1% 的读者愿意捐款，他们的付出帮助了 99% 的读者免费获取知识，我们在此表示感谢。