栈（综述）

                     

贡献者： 待更新

　　 （本文根据 CC-BY-SA 协议转载自原搜狗科学百科对英文维基百科的翻译）

　　 在计算机科学中，堆栈作为元素的集合是一种抽象数据类型，有两个主要操作：

• 推送，它将元素添加到集合中。
• pop，移除最近添加的尚未移除的元素。

　　 元素从堆栈中取出的顺序产生了它的另一个名字，叫做后进先出。此外，查看操作可以在不修改堆栈的情况下访问顶部。[1] 这种结构的名称 “堆栈” 来源于一组堆叠在一起的物理项目的类比，这使得从堆栈顶部取出一个项目变得容易，而到达堆栈中更深处的项目可能需要先取出多个上层的其他项目。[2]

　　 推送和弹出操作被视为线性数据结构，或者更抽象地说是顺序集合，只发生在结构的一端，即堆栈的顶部。这使得将堆栈实现为单个链表和指向顶部元素的指针成为可能。堆栈可以被实现为具有有限容量的空间。如果堆栈已满，并且没有足够的空间接受要推送的实体，则堆栈被认为处于溢出状态。弹出操作从堆栈顶部移除一个项目。

1. 历史

　　 斯塔克斯（Stacks）于 1946 年进入计算机科学文献，当时艾伦·图灵（Alan M. Turing）使用 “埋葬” 和 “不埋葬”（"bury" and "unbury"）这两个术语作为调用子程序和从子程序返回的手段。[3] 子程序已经于 1945 年在康拉德·楚泽的 Z4（Konrad Zuse's Z4）中实现。

　　 慕尼黑理工大学（Technical University Munich）的克劳斯·萨姆森（Klaus Samelson）和弗里德里希·鲍尔（Friedrich L. Bauer）于 1955 年提出了这个想法，并于 1957 年申请了专利，[4] 鲍尔（Bauer）于 1988 年 3 月因堆栈原理的发明获得了计算机先锋奖。[5] 澳大利亚人查尔斯·伦纳德·汉布林（Charles Leonard Hamblin）在 1954 年上半年独立发展了同样的概念。[6]

　　 堆栈通常被比喻成自助餐厅中弹簧加载的一堆盘子。[7][2][8] 干净的盘子放在堆叠的顶部，将任何已经在那里的盘子向下推。当一个盘子从堆叠中取出时，它下面的那个就会弹出来成为新的顶部。

2. 非必要操作

　　 在许多实现中，堆栈比 “推送” 和 “弹出” 有更多的操作。一个例子是 “栈顶”，即 “读取数据”，它观察最顶层的元素而不将其从栈中移除。[9] 由于这可以通过使用相同数据的 “弹出” 和 “推送” 来完成，所以这不是必需的。如果堆栈为空，“堆栈顶部” 操作可能会出现下溢情况，与 “弹出” 操作相同。此外，实现通常有一个函数用于返回堆栈是否为空。

3. 软件栈

3.1 实现

　　 堆栈可以通过数组或链表轻松实现。在这两种情况下，将数据结构标识为堆栈的不是实现，而是接口：只允许用户将项目弹出或推送到数组或链表上，几乎没有其他辅助操作。下面将使用伪代码演示这两种实现。

　　 数组 数组可用于实现（有界）堆栈，如下所示。第一个元素（通常在零点偏移处）是底部，导致数组[0]成为被推到堆栈上的第一个元素，最后一个元素弹出。程序必须跟踪堆栈的大小（长度），使用一个可变的顶部记录到目前为止推送的项目数，从而指向数组中下一个元素要插入的位置（假设从零开始的索引约定）。因此，堆栈本身可以有效地实现为三元素结构：

structure stack：
    maxsize ： integer
    top ： integer
    items ： array of item

procedure initialize（stk ： stack, size ： integer）：
    stk.items ← new array of size items, initially empty
    stk.maxsize ← size
    stk.top ← 0

在检查溢出后，推送（push）操作添加一个元素并递增顶部索引：

procedure push（stk ： stack, x ： item）：
    if stk.top = stk.maxsize：
        report overflow error
    else：
        stk.items[stk.top] ← x
        stk.top ← stk.top + 1

类似地，弹出（pop）在检查下溢后递减顶部索引，并返回先前的顶部索引：

procedure pop（stk ： stack）：
    if stk.top = 0：
        report underflow error
    else：
        stk.top ← stk.top − 1
        r ← stk.items[stk.top]
        return r

使用动态数组，有可能实现一个可以根据需要增长或收缩的堆栈。堆栈的大小就是动态数组的大小，这是一个非常有效的堆栈实现，因为向动态数组的末尾添加项目或从末尾移除项目需要摊销的 O（1）时间。

　　 链表

　　 实现堆栈的另一个选项是使用单链表。堆栈是指向列表 “头” 的指针，也许还有一个计数器来追踪列表的大小：

structure frame：
    data ： item
    next ： frame or nil

structure stack：
    head ： frame or nil
    size ： integer

procedure initialize（stk ： stack）：
    stk.head ← nil
    stk.size ← 0

推送和弹出项目出现在列表的最前面；在此实现中，溢出是不可能的（除非内存耗尽）：

procedure push（stk ： stack, x ： item）：
    newhead ← new frame
    newhead.data ← x
    newhead.next ← stk.head
    stk.head ← newhead
    stk.size ← stk.size + 1

procedure pop（stk ： stack）：
    if stk.head = nil：
        report underflow error
    r ← stk.head.data
    stk.head ← stk.head.next
    stk.size ← stk.size - 1
    return r

3.2 堆栈和编程语言

　　 一些语言，如 Perl、LISP、JavaScript 和 Python，使堆栈操作在它们的标准列表/数组类型中可以推送和弹出。有些语言，特别是第四类语言（包括 PostScript），是围绕程序员直接可见和操作的语言来定义堆栈的设计。

　　 以下是在公共 Lisp 中操作堆栈的示例（“>” 是 Lisp 解释器的提示；不以 “>” 开头的行是解释程序对表达式的响应）：

> (setf stack (list 'a 'b 'c))  ;; set the variable "stack"
(A B C)
> (pop stack)  ;; get top (leftmost) element, should modify the stack
A
> stack        ;; check the value of stack
(B C)
> (push 'new stack)  ;; push a new top onto the stack
(NEW B C)

一些 C++标准库容器类型具有带后进先出语义的推回和弹出（push_back 和 pop_back）操作；此外，堆栈模板类对现有的编辑库进行了调整，以便只提供推送/弹出（push/pop）操作的受限应用程序接口（API）。PHP 有一个 SplStack class。Java 的库包含一个堆栈类，它是向量的专门化。下面是一个使用该类的 Java 语言示例程序。

import java.util.*;

class StackDemo {
  public static void main(String[]args) {
    Stack<String> stack = new Stack<String>();
    stack.push("A");    // Insert "A" in the stack
    stack.push("B");    // Insert "B" in the stack
    stack.push("C");    // Insert "C" in the stack
    stack.push("D");    // Insert "D" in the stack
    System.out.println(stack.peek());    // Prints the top of the stack ("D")
    stack.pop();    // removing the top ("D")
    stack.pop();    // removing the next top ("C")
  }
}

4. 硬件堆栈

　　 堆栈在架构级别的一个常见用途是作为分配和访问内存的一种方法。

4.1 堆栈的基本架构

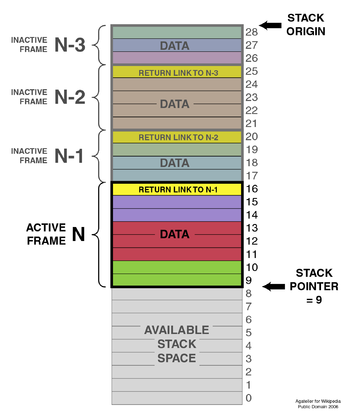
　　 一个典型的堆栈是一个具有固定原点和可变大小的计算机内存区域。最初堆栈的大小为零。堆栈指针通常以硬件寄存器的形式指向堆栈上最近引用的位置；当堆栈的大小为零时，堆栈指针指向堆栈的原点。

　　 适用于所有堆栈的两个操作是：

• 推送操作，其中数据项被放置在堆栈指针所指向的位置，并且堆栈指针中的地址被数据项的大小调整；
• 弹出或拉取操作：堆栈指针指向的当前位置的数据项被移除，堆栈指针根据数据项的大小进行调整。

　　 堆栈操作的基本原理有许多变化。每个堆栈在内存中都有一个固定的开始位置。当数据项被添加到堆栈中时，堆栈指针被移动以指示堆栈的当前范围，该范围从原点开始扩展。

　　 堆栈指针可以指向堆栈的原点，或者指向原点之上或之下的有限范围的地址（取决于堆栈增长的方向）；但是，堆栈指针不能越过堆栈的原点。换句话说，如果堆栈的原点在地址 1000 并且堆栈向下增长（指向地址 999、998 等），堆栈指针决不能增加超过 1000（至 1001、1002 等）。如果堆栈上的弹出操作导致堆栈指针移过堆栈的原点，就会发生堆栈下溢。如果推送操作导致堆栈指针增加或减少超过堆栈的最大范围，就会发生堆栈溢出。

　　 一些严重依赖堆栈的环境可能会提供额外的操作，例如：

• 重复：顶部项目被弹出，然后被再次推（两次），这样前一个顶部项目的附加副本此时位于顶部，原始副本在它下面。
• Peek：检查（或返回）最上面的项目，但是堆栈指针和堆栈大小不变（意味着该项目保留在堆栈中）。在许多文章中，这也被称为 Top 操作。
• 交换或交换：堆栈上最上面的两个项目交换位置。
• 旋转（或滚动）：n 个最上面的项目以旋转方式在堆栈上移动。例如，如果 $n=3$，堆栈上的项目 1、2 和 3 将分别移动到堆栈上的位置 2、3 和 1。这种操作的许多变体都是可能的，最常见的叫做左旋转和右旋转。

　　 堆栈通常是自下而上的可视化增长（就像真实世界的堆栈一样）。它们也可以从左向右生长，这样 “最上面的” 变成 “最右边的”，甚至从上到下生长。重要的特征是堆栈的底部在一个固定的位置。本节中的图示是自上而下增长可视化的示例：顶部（28）是堆栈 “底部”，因为堆栈 “顶部”（9）是项目被推或弹出的地方。

　　 向右旋转将第一个元件移动到第三个位置，第二个移动到第一个位置，第三个移动到第二个位置。下面是这个过程的两个等效可视化演示：

apple                         banana
banana    ===right rotate==>  cucumber
cucumber                      apple

cucumber                      apple
banana    ===left rotate==>   cucumber
apple                         banana

在计算机中，堆栈通常由一块存储单元表示，其中 “底部” 位于固定位置，堆栈指针保存堆栈中当前 “顶部” 单元的地址。不管堆栈实际上是朝着较低的内存地址还是朝着较高的内存地址增长，都使用顶部和底部术语。

　　 将一个项目推到堆栈上会根据项目的大小调整堆栈指针（根据堆栈在内存中的增长方向，可以递减或递增），将其指向下一个单元格，并将新的顶部项目复制到堆栈区域。这取决于具体的实现，在推送操作结束时，堆栈指针可以指向堆栈中的下一个未使用的位置，或者它可以指向堆栈中最顶端的项。如果堆栈指向当前最顶端的项目，堆栈指针将在新项目被推送到堆栈之前更新；如果它指向堆栈中的下一个可用位置，它将在新项目被推送到堆栈后更新。

　　 弹出堆栈只是推入的逆过程。堆栈中最顶端的项被移除，堆栈指针被更新，其顺序与推送操作中使用的顺序相反。

　　 主存储器中的堆栈

　　 许多 CISC 类型的中央处理器设计，包括 x86、Z80 和 6502，都有一个专用寄存器用作调用堆栈指针，带有隐式更新专用寄存器的专用调用、返回、推送和弹出指令，从而增加代码密度。一些 CISC 处理器，如 PDP-11 和 68000，也有特殊的堆栈实现寻址模式，通常也有一个半专用的堆栈指针（如 68000 中的 A7）。相比之下，大多数精简指令集处理器的设计没有专用的堆栈指令，大多数寄存器（并不是全部）都可以根据需要用作堆栈指针。

　　 寄存器或专用存储器中的堆栈

　　 x87 浮点架构是一组寄存器的示例，这些寄存器被组织为堆栈，其中也可以直接访问单个寄存器（相对于当前顶部）。一般来说，与基于堆栈的计算机一样，将堆栈顶部作为隐式参数允许使用总线带宽和代码高速缓存的小机器代码占用空间，但这也阻止了某些类型的处理器优化，这些处理器允许所有（两个或三个）操作数随机访问寄存器文件。尽管这种方法仍然是可行的，但是堆栈结构也使得带有重命名的寄存器（用于推测性执行）的超标量实现更加复杂，如现代 x87 的实现所示。

　　 Sun SPARC、AMD Am29000 和英特尔 i960 都是使用寄存器堆栈中的寄存器窗口作为另一种策略来避免使用慢速主存储器来处理函数参数和返回值的架构示例。

　　 还有许多小型微处理器直接在硬件中实现堆栈，一些微控制器具有固定深度的堆栈，无法直接访问，如 PIC 微控制器、计算机牛仔 MuP21、哈里斯 RTX 线和诺维克 NC4016。许多基于堆栈的微处理器被用来在微码级实现 Forth 编程语言。堆栈也被用作许多大型机和微型计算机的基础。这种机器被称为堆叠机，最著名的是伯罗斯（Burroughs）B5000。

5.3 编译时内存管理

　　 许多编程语言都是面向堆栈的，这意味着它们将大多数基本操作（添加两个数字，打印一个字符）定义为从堆栈中获取参数，并将任何返回值放回堆栈中。例如，PostScript 有一个返回堆栈和一个操作数堆栈，还有一个图形状态堆栈和一个字典堆栈。许多虚拟机也是面向堆栈的，包括 p 代码机和 Java 虚拟机。

　　 几乎所有的调用约定-子程序的方法都是子程序接收参数并返回结果给一个特殊堆栈（“调用堆栈”）来保存关于过程/函数调用和嵌套的信息，以便在调用结束时切换到被调用函数的上下文并恢复到调用函数。这些函数遵循调用方和被调用方之间的运行时协议来保存参数并在堆栈上返回值。堆栈是支持嵌套或递归函数调用的重要方式。编译器隐式使用这种类型的堆栈来支持 CALL 和 RETURN 语句（或它们的等效语句），而不是程序员直接操作。

　　 一些编程语言使用堆栈来存储过程本地的数据。当进入过程时，本地数据项的空间从堆栈中分配，当过程退出时从堆栈中释放。C 语言通常以这种方式实现。对数据和过程调用使用相同的堆栈具有重要的安全含义（见下文），程序员必须意识到这一点，以避免在程序中引入严重的安全漏洞。

5.4 高效算法

　　 一些算法使用堆栈（不同于大多数编程语言通常的函数调用堆栈）作为组织信息的主要数据结构。其中包括：

• 格雷厄姆（Graham）扫描，一种二维点系统的凸包算法。输入子集的凸包被保存在堆栈中，当一个新点被添加到凸包中时，该堆栈用于查找和移除边界中的凹点。[10]
• SMAWK 算法用于查找单调矩阵的行最小值，其中一部分使用与 Graham 扫描类似的方式进行堆栈。[11]
• 所有最近的较小值，对于数组中的每一个数，寻找比它小的最近的前一个数的问题。解决此问题的一种算法就是使用堆栈来维护最近的较小值的候选集合。对于数组中的每个位置，都会弹出堆栈，直到在其顶部找到一个较小的值，然后将新位置的值推入堆栈。[12]
• 最近邻链算法是一种基于保持一个集群堆栈的凝聚层次聚类方法，每个集群都是其在堆栈上的最近邻。当该方法找到一对相互最近的聚类时，它们会被弹出并合并。[13]

5. 安全

　　 一些计算环境使用堆栈的方式可能会使它们容易受到安全漏洞和攻击。在这种环境中工作的程序员必须特别小心，以避免这些陷阱产生不利的影响。

　　 例如，一些编程语言使用公共堆栈来存储被过程调用的本地数据并且允许该过程将链接信息返回给调用方。这意味着程序将数据移入和移出包含过程调用的关键返回地址的同一堆栈。如果数据移动到堆栈上的错误位置，或者过大的数据项移动到不足以容纳它的堆栈位置，则过程调用的返回信息可能会被损坏，从而导致程序失败。

　　 恶意方可能试图通过向不检查输入长度的程序提供过大的数据输入，从而利用这种类型的实现进行堆栈粉碎攻击。这样的程序可以将数据完整地复制到堆栈上的一个位置，这样做可以改变调用它的过程的返回地址。攻击者可以尝试找到可以提供给这种程序的特定类型的数据，从而重置当前过程的返回地址，以指向堆栈本身（以及攻击者提供的数据）中的一个区域，该区域中又包含了执行未授权的操作指令。

　　 这种类型的攻击是缓冲区溢出攻击的一种变体，并且是软件中安全漏洞的极其频繁的来源，主要是因为一些最流行的编译器对数据和过程调用都使用共享堆栈，并且不验证数据项的长度。程序员通常也不编写代码来验证数据项的大小，当过大或过小的数据项被复制到堆栈时，就可能会发生安全漏洞。

6. 参考文献

　　 [1] ^By contrast, a simple QUEUE operates FIFO (first in, first out)..

　　 [2] ^Cormen, Thomas H.（英语：Thomas H. Cormen）; Leiserson, Charles E. ; Rivest, Ronald L.; Stein, Clifford (2009) [1990]. Introduction to Algorithms (3rd ed.). MIT Press and McGraw-Hill. ISBN 0-262-03384-4.CS1 maint: Multiple names: authors list (link).

　　 [3] ^Carpenter, B. E.; Doran, R. W. (January 1977). "The other Turing machine". The Computer Journal. 20 (3): 269–279. doi:10.1093/comjnl/20.3.269..

　　 [4] ^Dr. Friedrich Ludwig Bauer and Dr. Klaus Samelson (30 March 1957). "Verfahren zur automatischen Verarbeitung von kodierten Daten und Rechenmaschine zur Ausübung des Verfahrens" (in german). Germany, Munich: Deutsches Patentamt. Retrieved 2010-10-01.CS1 maint: Unrecognized language (link).

　　 [5] ^IEEE-Computer-Pioneer-Preis -- Bauer, Friedrich L., Technical University of Munich, Faculty of Computer Science, (1 January 1989)..

　　 [6] ^C. L. Hamblin, "An Addressless Coding Scheme based on Mathematical Notation", N.S.W University of Technology, May 1957 (typescript).

　　 [7] ^Ball, John A. (1978). Algorithms for RPN calculators (1 ed.). Cambridge, Massachusetts, USA: Wiley-Interscience, John Wiley & Sons, Inc. ISBN 978-0-471-03070-6..

　　 [8] ^Godse, A. P.; Godse, D. A. (2010-01-01). Computer Architecture. Technical Publications. pp. 1–56. ISBN 9788184315349. Retrieved 2015-01-30..

　　 [9] ^Horowitz, Ellis: "Fundamentals of Data Structures in Pascal", page 67. Computer Science Press, 1984.

　　 [10] ^Graham, R.L. (1972). An Efficient Algorithm for Determining the Convex Hull of a Finite Planar Set. Information Processing Letters 1, 132-133.

　　 [11] ^Aggarwal, Alok; Klawe, Maria M.; Moran, Shlomo; Shor, Peter; Wilber, Robert (1987), "Geometric applications of a matrix-searching algorithm", Algorithmica, 2 (2): 195–208, doi:10.1007/BF01840359, MR 0895444..

　　 [12] ^Berkman, Omer; Schieber, Baruch; Vishkin, Uzi (1993), "Optimal doubly logarithmic parallel algorithms based on finding all nearest smaller values", Journal of Algorithms, 14 (3): 344–370, CiteSeerX 10.1.1.55.5669, doi:10.1006/jagm.1993.1018..

　　 [13] ^Murtagh, Fionn (1983), "A survey of recent advances in hierarchical clustering algorithms" (PDF), The Computer Journal, 26 (4): 354–359, doi:10.1093/comjnl/26.4.354..