整数（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章

图
图 1：排列在数轴上的整数

　　 整数是指 零（0）、正自然数（1, 2, 3,…），或 正自然数的相反数（−1, −2, −3,…）。\(^\text{[1]}\) 正自然数的相反数（或加法逆元）称为负整数。\(^\text{[2]}\) 所有整数构成的集合通常记作 粗体 \(\mathbf{Z}\) 或 黑板粗体：$\mathbb{Z}$.\(^\text{[3][4]}\)

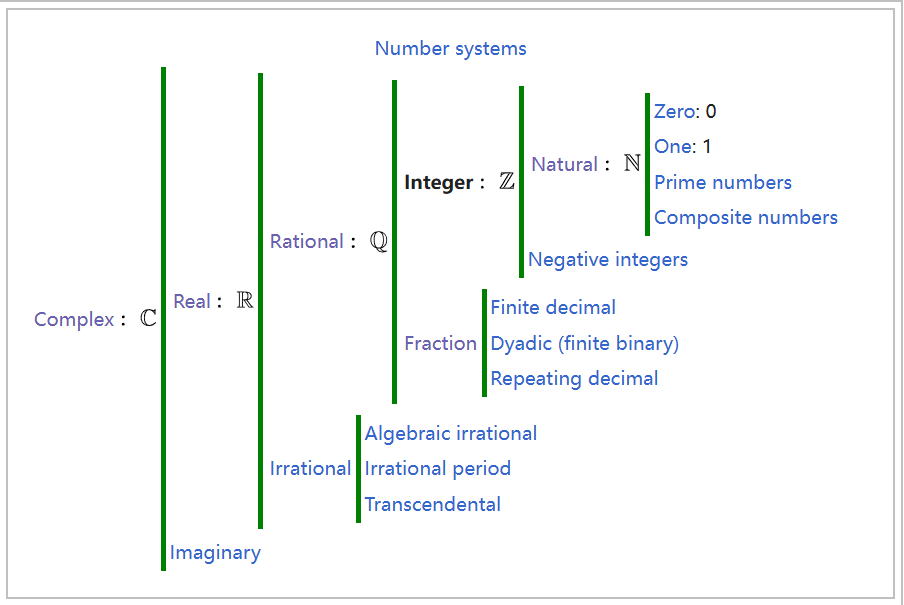
　　 自然数集合 $\mathbb{N}$ 是整数集合 $\mathbb{Z}$ 的子集，而 $\mathbb{Z}$ 又是有理数集合 $\mathbb{Q}$ 的子集，而 $\mathbb{Q}$ 本身是实数集合 $\mathbb{R}$ 的子集。\(^\text{[a]}\) 与自然数集合类似，整数集合 $\mathbb{Z}$ 是可数无限集。整数可以被视为一种实数，其表示中不含分数部分。例如：$21, 4, 0, -2048$ 都是整数；而 $9.75, 5+\tfrac{1}{2}, \tfrac{5}{4}, \sqrt{2}$ 都不是整数。\(^\text{[7]}\)

　　 整数构成了包含自然数的最小的群与最小的环。在代数数论中，整数有时被称为有理整数，以区别于更一般的代数整数。实际上，（有理）整数就是那些既是代数整数、又是有理数的数。

1. 历史

　　 integer 一词源自拉丁语 integer，意为 “完整的” 或（字面意义上）“未触碰的”，由 in（“不”）+ tangere（“触碰”）组成。英语单词 entire 也来自同一词源，经由法语 entier（既表示 “完整的”，也表示 “整数”）。\(^\text{[8]}\) 在历史上，该词曾被用于表示 1 的倍数 \(^\text{[9][10]}\)，或者表示带分数的整数部分。\(^\text{[11][12]}\) 当时仅考虑正整数，因此该词与自然数同义。随着负数的实用性被逐渐认识到，整数的定义才扩展到包括负数。\(^\text{[13]}\) 例如，莱昂哈德·欧拉在其 1765 年的《代数学原理》中，就将整数定义为既包含正数也包含负数。\(^\text{[14]}\)

　　 “整数集合” 这一说法在 19 世纪末之前并未使用。随着格奥尔格·康托尔引入无限集合与集合论，该说法才出现。用字母 $Z$ 表示整数集合，来源于德语单词 Zahlen（“数”）\(^\text{[3][4]}\)，这一记号常被归功于大卫·希尔伯特。\(^\text{[15]}\) 该符号在教材中最早出现于 1947 年由布尔巴基学派（Nicolas Bourbaki 集体笔名）编写的《代数学》中。\(^\text{[3][16]}\) 但该记号并未立即被普遍接受。例如，有的教材使用字母 J，\(^\text{[17]}\) 而 1960 年的一篇论文用 $Z$ 表示非负整数。\(^\text{[18]}\) 然而，到 1961 年，现代代数学教材中普遍使用 $Z$ 表示包含正负整数的集合。\(^\text{[19]}\)

　　 符号 $\mathbb{Z}$ 常带上标或下标以表示不同的整数集合，不同作者用法可能不同：$\mathbb{Z}^{+}, \mathbb{Z}_{+}, \mathbb{Z}^{>}$：正整数 $\mathbb{Z}^{0+}, \mathbb{Z}^{\geq}$：非负整数 $\mathbb{Z}^{\neq}$：非零整数 $\mathbb{Z}^{*}$：有些作者表示非零整数，有些表示非负整数，还有些表示 $\{-1, 1\}$（即 $\mathbb{Z}$ 的单位元群） $\mathbb{Z}_p$：可能表示模 $p$ 的整数集合（即整数的同余类集合），也可能表示 $p$-进制整数集合。\(^\text{[20][21]}\)

　　 直到 1950 年代初期，whole numbers（全体数）一词还被认为与整数同义。\(^\text{[22][23][24]}\) 在 1950 年代末期，作为 “新数学运动” 的一部分，美国小学教师开始教授 whole numbers 指自然数（不含负数），而 integer 则包括负数。\(^\text{[26][27]}\) 直到今天，whole numbers 一词仍然存在歧义。\(^\text{[28]}\)

2. 代数性质

图
图 2：整数可以被看作是在一条无限长数轴上离散的、等间距的点。在上图中，非负整数以蓝色表示，负整数以红色表示。

　　 像自然数一样，$\mathbb{Z}$ 在加法和乘法运算下是封闭的，也就是说，任意两个整数的和与积仍然是整数。然而，由于包含了负自然数（以及重要的 0），$\mathbb{Z}$ 与自然数不同，它在减法下也是封闭的。\(^\text{[29]}\)

　　 整数构成了一个环，并且在以下意义上是最基本的环：对任意一个环，都存在一个从整数映射到该环的唯一环同态。这一普遍性质，即在环范畴中作为一个初始对象，刻画了环 $\mathbb{Z}$。

　　 这个唯一的同态是单射，当且仅当该环的特征数为零。因此，任何特征为零的环都包含一个与 $\mathbb{Z}$ 同构的子环，这个子环就是它的最小子环。$\mathbb{Z}$ 在除法下并不封闭，因为两个整数的商（例如 \(1 \boldsymbol{\nabla}\boldsymbol{\cdot} 2\)）不一定是整数。虽然自然数在 乘方（指数运算）下是封闭的，但整数却不是（因为当指数为负时，结果可能是分数）。

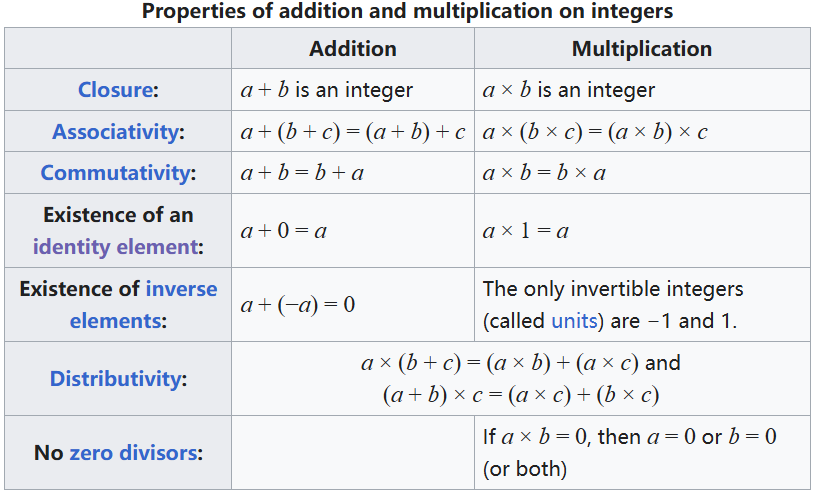
　　 下表列出了整数加法和乘法的一些基本性质（适用于任意整数 \(a, b, c\)）：

图
图 3

　　 前面所列出的关于加法的前五条性质表明：$\mathbb{Z}$ 在加法下是一个阿贝尔群。它还是一个 循环群，因为任意非零整数都可以写成有限次的 $1+1+\cdots+1$ 或 $(-1)+(-1)+\cdots+(-1)$ 的形式。事实上，$\mathbb{Z}$ 在加法下是唯一的无限循环群，即任何无限循环群都与 $\mathbb{Z}$ 同构。

　　 前面所列出的关于乘法的前四条性质表明：$\mathbb{Z}$ 在乘法下是一个交换幺半群。然而，并非每个整数都有乘法逆元（例如 2 就没有），这意味着 $\mathbb{Z}$ 在乘法下并不是一个群。

　　 把上述性质表中的所有规则（除了最后一条）合并在一起，可以得出：$\mathbb{Z}$ 连同加法与乘法一起，构成了一个带有单位元的交换环。它是所有此类代数结构的原型。在 $\mathbb{Z}$ 中对所有变量值都成立的等式，也必然在任意带单位的交换环中成立。某些非零整数在某些环中可能映射为零。

　　 整数中不存在零因子（即性质表中的最后一条），这意味着交换环 $\mathbb{Z}$ 是一个整环。整数缺乏乘法逆元，这等价于 $\mathbb{Z}$ 在除法下不封闭，因此 $\mathbb{Z}$ 不是一个域。包含整数作为子环的最小域是有理数域。从整数构造有理数的过程，可以推广为从任意整环构造其分式域。反过来，从一个代数数域（即有理数的代数扩张）出发，可以得到其整数环，其中包含 $\mathbb{Z}$ 作为其子环。

　　 虽然普通的除法在 $\mathbb{Z}$ 上没有定义，但带余除法 是在整数上定义的。这就是欧几里得除法，并具有以下重要性质：给定两个整数 $a$ 和 $b$（其中 $b \neq 0$），存在唯一的整数 $q$ 与 $r$，使得：$a = q \times b + r, \quad 0 \leq r < |b|$，其中 $|b|$ 表示 $b$ 的绝对值。整数 $q$ 称为商，整数 $r$ 称为余数。计算最大公约数的欧几里得算法就是通过一系列欧几里得除法实现的。

　　 综上所述，$\mathbb{Z}$ 是一个欧几里得整环。这进一步意味着 $\mathbb{Z}$ 是一个主理想整环，并且任意正整数都可以以本质唯一的方式分解为素数的乘积。\(^\text{[30]}\) 这就是著名的算术基本定理。

3. 序理论性质

　　 $\mathbb{Z}$ 是一个全序集，且没有上界或下界。整数的排序方式为：$\cdots < -3 < -2 < -1 < 0 < 1 < 2 < 3 < \cdots$ 一个整数若大于零，则称为正数；若小于零，则称为负数。零既不是正数，也不是负数。

　　 整数的次序与代数运算是相容的，具体表现为：

  1. 如果 $a < b$ 且 $c < d$，则有 $a + c < b + d$
  2. 如果 $a < b$ 且 $0 < c$，则有 $ac < bc$

　　 因此，整数集合 $\mathbb{Z}$ 连同上述次序构成一个有序环。

　　 整数是唯一一个非平凡的全序阿贝尔群，其正元素是良序的。\(^\text{[31]}\) 这等价于以下叙述：任意诺特赋值环要么是一个域，要么是一个离散赋值环。

4. 构造

传统构造

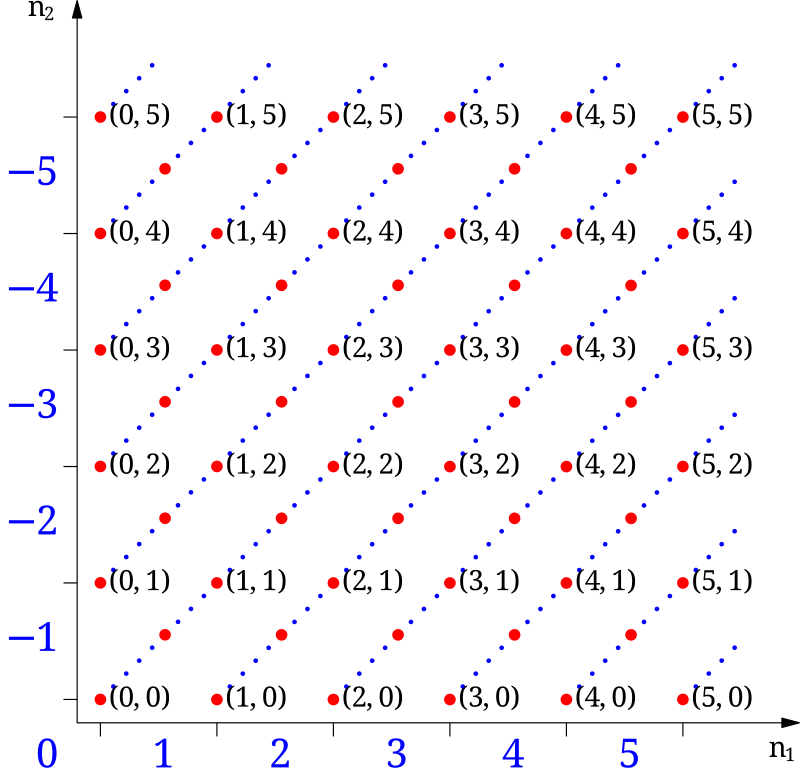
　　 在小学教学中，整数常常被直观地定义为：（正）自然数、零以及自然数的相反数的并集。这一思想可以形式化为如下步骤。\(^\text{[32]}\) 首先，根据皮亚诺公理 构造自然数集合，记作：$P$ 然后，构造一个集合 $P^{-}$ 它与 $P$ 不相交，并且通过一个函数 $\psi$ 与 $P$ 建立一一对应。例如，可以取 $P^{-} = \{(1,n) \mid n \in P\}$，并定义映射 $\psi : n \mapsto (1,n)$.最后，引入一个不属于 $P$ 或 $P^{-}$ 的元素作为零，例如 $0 = (0,0)$.于是，整数被定义为：$P \;\cup\; P^{-} \;\cup\; \{0\}$.

　　 在此基础上，可以对整数分情况定义传统的算术运算（分别针对正数、负数与零）。 例如，取负运算定义如下： $$ -x = \begin{cases} \psi(x), & \text{若 } x \in P, \\[6pt] \psi^{-1}(x), & \text{若 } x \in P^{-}, \\[6pt] 0, & \text{若 } x = 0. \end{cases}~ $$ 这种传统风格的定义方式会导致出现许多不同情况（每个算术运算都需要针对整数的不同类型分别定义），从而使得证明整数满足各种算术定律变得相当繁琐。\(^\text{[33]}\)

有序对的等价类

图
图 4：红点表示自然数的有序对。相连的红点构成等价类，这些等价类在数轴末端对应为蓝色的整数。

　　 在现代集合论数学中，常常使用一种更加抽象的构造方法 \(^\text{[34][35]}\) 这种方法允许在不区分情况的前提下定义算术运算。\(^\text{[36]}\) 因此，整数可以形式化地构造为自然数有序对 $(a,b)$ 的等价类。\(^\text{[37]}\)

　　 直观上，$(a,b)$ 表示从 $a$ 中减去 $b$ 的结果。\(^\text{[37]}\) 为了确认 $1-2$ 和 $4-5$ 表示相同的数，我们在这些有序对上定义一个等价关系 $\sim$，规则如下： $$(a,b) \sim (c,d)~$$ 当且仅当 $$a+d = b+c~$$. 利用自然数上的运算，可以定义整数的加法与乘法。若用 $[(a,b)]$ 表示包含 $(a,b)$ 的等价类，则有：加法： $$ [(a,b)] + [(c,d)] := [(a+c,\, b+d)].~ $$ 乘法： $$ [(a,b)] \cdot [(c,d)] := [(ac+bd,\, ad+bc)].~ $$ 取负（加法逆元）： $$ -[(a,b)] := [(b,a)].~ $$ 减法（定义为加法逆元的加法）： $$ [(a,b)] - [(c,d)] := [(a+d,\, b+c)].~ $$ 整数的标准次序可以定义为： $$ [(a,b)] < [(c,d)] \quad \text{当且仅当} \quad a+d < b+c.~ $$ 很容易验证，这些定义与所选等价类代表元的具体选择无关。

　　 每一个等价类都有一个唯一的成员，其形式为 $(n,0)$ 或 $(0,n)$（有时两者同时出现）。 自然数 $n$ 被识别为等价类 $[(n,0)]$（也就是说，自然数通过映射 $n \mapsto [(n,0)]$ 嵌入到整数中），而等价类 $[(0,n)]$ 被记作 $-n$（这涵盖了所有剩余的等价类，并且再次给出了 $[(0,0)]$，因为 $-0 = 0$）。

　　 因此，$[(a,b)]$ 可以记作： $$ \begin{cases} a-b, & \text{若 } a \geq b \\[6pt] -(b-a), & \text{若 } a < b \end{cases}~ $$ 如果自然数已被识别为相应的整数（通过上面提到的嵌入），这种记号不会产生歧义。

　　 这种记号恢复了人们熟悉的整数表示：$\{ \ldots, -2, -1, 0, 1, 2, \ldots \}$.

　　 一些例子如下： $$ \begin{aligned} 0 &= [(0,0)] = [(1,1)] = \cdots = [(k,k)] \\[6pt] 1 &= [(1,0)] = [(2,1)] = \cdots = [(k+1,k)] \\[6pt] -1 &= [(0,1)] = [(1,2)] = \cdots = [(k,k+1)] \\[6pt] 2 &= [(2,0)] = [(3,1)] = \cdots = [(k+2,k)] \\[6pt] -2 &= [(0,2)] = [(1,3)] = \cdots = [(k,k+2)] \end{aligned}~ $$

其他构造方法

　　 在理论计算机科学中，自动定理证明器和项重写引擎常常使用其他方式来构造整数。整数被表示为代数项，这些代数项由一些基本运算（例如 zero、succ（后继）、pred（前驱））和自然数组成，而自然数则假定已经通过皮亚诺构造得到。

　　 目前至少存在十种以上有符号整数的构造方法。\(^\text{[38]}\) 这些构造方法在多个方面存在差异：用于构造的基本运算的数量；运算符元数（通常在 0 到 2 之间）；这些运算所接受的参数类型；是否允许自然数作为某些运算的参数；这些运算是否为自由构造子——也就是说，某个整数是否只能用唯一的代数项表示，还是可以有多个不同的表示。

　　 前一节介绍的整数构造方法对应于一种特殊情况：只有一个基本运算 $(x,y)$ 它以两个自然数 $x$ 和 $y$ 作为参数，并返回一个整数（即 $x-y$）。这种运算不是自由的，因为整数 $0$ 可以表示为 $\text{pair}(0,0)$，也可以表示为 $\text{pair}(1,1)$，$\text{pair}(2,2)$，等等。

　　 这种构造方法被证明助手 Isabelle 所采用；然而，许多其他工具使用不同的构造方法，尤其是基于自由构造子的方法，它们更简单，并且在计算机中实现起来效率更高。

5. 计算机科学

　　 在计算机语言中，整数通常是一个原始数据类型。然而，整数数据类型只能表示整数集合的一个有限子集，因为实际计算机的容量有限。在常见的二进制补码表示中，符号位的定义区分的是 “负数” 和 “非负数”，而不是 “负数、正数和零”。（不过，计算机当然可以判断一个整数值是否真正为正数。）定长的整数近似数据类型（或其子集），在多种编程语言（如 Algol68、C、Java、Delphi 等）中记作 int 或 Integer。

　　 可变长度的整数表示方式（如 bignums）能够存储任意大小的整数，只要它能放入计算机内存。 其他整数数据类型通常以固定大小实现，常见的是位数为 $2$ 的幂（如 4 位、8 位、16 位等），或容易记忆的十进制位数（如 9 位或 10 位）。

6. 基数

　　 整数集合是可数无限集，意味着可以将每个整数与一个唯一的自然数配对。例如，下面是一种配对方式： $$ (0,1),\; (1,2),\; (-1,3),\; (2,4),\; (-2,5),\; (3,6), \;\ldots,\; (1-k,\, 2k-1),\; (k,\, 2k), \;\ldots~ $$ 更严格地说，整数集合 $\mathbb{Z}$ 的基数等于 $\aleph_0 \quad (\text{阿列夫零, aleph-null})$,$\mathbb{Z}$ 与 $\mathbb{N}$ 之间的这种配对关系称为双射。

7. 另见

图
图 5

8. 脚注

　　 a.更准确地说，每一个数系都被嵌入到下一个数系中，并同构地映射到其中的一个子集。\(^\text{[5]}\) 通常假定的集合论包含关系，可以通过以下方式得到：先构造实数，然后舍弃之前的构造，并将其他数集定义为实数的子集。\(^\text{[6]}\)

9. 参考文献

  1. Science and Technology Encyclopedia. University of Chicago Press. 2000 年 9 月，第 280 页. ISBN 978-0-226-74267-0.
  2. Hillman, Abraham P.; Alexanderson, Gerald L. (1963). Algebra and Trigonometry. Boston: Allyn and Bacon.
  3. Miller, Jeff (2010 年 8 月 29 日). “Earliest Uses of Symbols of Number Theory”. 2010 年 1 月 31 日存档. 2010 年 9 月 20 日检索.
  4. Peter Jephson Cameron (1998). Introduction to Algebra. Oxford University Press. 第 4 页. ISBN 978-0-19-850195-4. 2016 年 12 月 8 日存档. 2016 年 2 月 15 日检索.
  5. Partee, Barbara H.; Meulen, Alice ter; Wall, Robert E. (1990 年 4 月 30 日). Mathematical Methods in Linguistics. Springer Science & Business Media. 第 78–82 页. ISBN 978-90-277-2245-4.（自然数本身并不是整数的集合论表示的子集；相反，整数集合包含一个由非负整数构成的子集，它与自然数集同构。）
  6. Wohlgemuth, Andrew (2014 年 6 月 10 日). Introduction to Proof in Abstract Mathematics. Courier Corporation. 第 237 页. ISBN 978-0-486-14168-8.
  7. Kaplan Test Prep (2019 年 6 月 4 日). GMAT Complete 2020: The Ultimate in Comprehensive Self-Study for GMAT. Simon and Schuster. ISBN 978-1-5062-4844-8.
  8. Evans, Nick (1995). “A-Quantifiers and Scope”. 见 Bach, Emmon W. (编). Quantification in Natural Languages. Dordrecht, The Netherlands; Boston, MA: Kluwer Academic Publishers. 第 262 页. ISBN 978-0-7923-3352-4.
  9. Smedley, Edward; Rose, Hugh James; Rose, Henry John (1845). Encyclopædia Metropolitana. B. Fellowes. 第 537 页.（“整数是单位的倍数”）
  10. Encyclopaedia Britannica 1771 年版，第 367 页. 好的，我来翻译这段参考文献，并保持原文格式与注释：
  11. Pisano, Leonardo; Boncompagni, Baldassarre（转写）(1202). Incipit liber Abbaci compositus to Lionardo filio Bonaccii Pisano in year Mccij [《计算之书》 (*The Book of Calculation*)]（手稿，拉丁文）. 译者：Sigler, Laurence E. Museo Galileo. 第 30 页.
    Nam rupti uel fracti semper ponendi sunt post integra, quamuis prius integra quam rupti pronuntiari debeant.【译文】分数应始终写在整数之后，虽然在读的时候应先读整数，再读分数。
  12. Encyclopaedia Britannica 1771 年版，第 83 页.
  13. Martinez, Alberto (2014). Negative Math*. Princeton University Press. 第 80–109 页.
  14. Euler, Leonhard (1771). Vollständige Anleitung Zur Algebra[《代数学引论》]（德文）. 第 1 卷，第 10 页.
    Alle diese Zahlen, so wohl positive als negative, führen den bekannten Nahmen der gantzen Zahlen, welche also entweder größer oder kleiner sind als nichts. Man nennt dieselbe gantze Zahlen, um sie von den gebrochenen, und noch vielerley andern Zahlen, wovon unten gehandelt werden wird, zu unterscheiden.【译文】所有这些数，不论正数还是负数，都称为 “整数”，它们要么大于零，要么小于零。我们称它们为整数，以区别于分数以及稍后将讨论的其他多种数。
  15. The University of Leeds Review. 第 31–32 卷. University of Leeds. 1989 年. 第 46 页.（顺带提及：符号 Z 来自德语 “Zahl”，由希尔伯特创造）。
  16. Bourbaki, Nicolas (1951). Algèbre, 第 1 章（法文，第 2 版）. Paris: Hermann. 第 27 页.Le symétrisé de N se note Z; ses éléments sont appelés entiers rationnels.【译文】自然数的对称化记作 Z；其元素称为有理整数。
  17. Birkhoff, Garrett (1948). Lattice Theory（修订版）. American Mathematical Society. 第 63 页.（其中提及整数集合 J）。
  18. Society, Canadian Mathematical (1960). Canadian Journal of Mathematics. Canadian Mathematical Society. 第 374 页.（考虑非负整数集合 $Z$）。
  19. Bezuszka, Stanley (1961). Contemporary Progress in Mathematics: Teacher Supplement [to] Part 1 and Part 2. Boston College. 第 69 页.（现代代数学教材通常用大写字母 Z 表示整数集合）。
  20. Keith Pledger and Dave Wilkins, Edexcel AS and A Level Modular Mathematics: Core Mathematics 1. Pearson, 2008.
  21. L. K. Turner, F. J. Budden, D. Knighton, Advanced Mathematics, Book 2, Longman, 1975.
  22. Mathews, George Ballard (1892). Theory of Numbers. Deighton, Bell and Company. 第 2 页.
  23. Betz, William (1934). Junior Mathematics for Today. Ginn.（整数或全体数，当按其自然顺序排列如 1, 2, 3 时，称为连续整数）。
  24. Peck, Lyman C. (1950). Elements of Algebra*. McGraw-Hill. 第 3 页.（由此产生的数称为正整数或正全体数）。
  25. Hayden, Robert (1981). A history of the "new math" movement in the United States(博士论文). Iowa State University. 第 145 页. doi:10.31274/rtd-180813-5631.（向中学教师和管理人员传播 “新数学” 消息的更有影响力的力量是美国全国数学教师协会（NCTM））。
  26. The Growth of Mathematical Ideas, Grades K-12: 24th Yearbook. National Council of Teachers of Mathematics. 1959 年. 第 14 页. ISBN 9780608166186.
  27. Deans, Edwina (1963). Elementary School Mathematics: New Directions. U.S. Department of Health, Education, and Welfare, Office of Education. 第 42 页.
  28. “entry: whole number”. The American Heritage Dictionary. HarperCollins.
  29. “Integer | mathematics”. Encyclopedia Britannica. 2020 年 8 月 11 日检索.
  30. Lang, Serge (1993). Algebra (第 3 版). Addison-Wesley. 第 86–87 页. ISBN 978-0-201-55540-0.
  31. Warner, Seth (2012). Modern Algebra. Dover Books on Mathematics. Courier Corporation. 定理 20.14, 第 185 页. ISBN 978-0-486-13709-4. 2015 年 9 月 6 日存档. 2015 年 4 月 29 日检索.
  32. Mendelson, Elliott (1985). Number Systems and the Foundations of Analysis. Malabar, Fla.: R.E. Krieger Pub. Co. 第 153 页. ISBN 978-0-89874-818-5.
  33. Mendelson, Elliott (2008). Number Systems and the Foundations of Analysis. Dover Books on Mathematics. Courier Dover Publications. 第 86 页. ISBN 978-0-486-45792-5. 2016 年 12 月 8 日存档. 2016 年 2 月 15 日检索.
  34. Ivorra Castillo: Álgebra.
  35. Kramer, Jürg; von Pippich, Anna-Maria (2017). From Natural Numbers to Quaternions (第 1 版). 瑞士: Springer Cham. 第 78–81 页. doi:10.1007/978-3-319-69429-0. ISBN 978-3-319-69427-6.
  36. Frobisher, Len (1999). Learning to Teach Number: A Handbook for Students and Teachers in the Primary School. The Stanley Thornes Teaching Primary Maths Series. Nelson Thornes. 第 126 页. ISBN 978-0-7487-3515-0. 2016 年 12 月 8 日存档. 2016 年 2 月 15 日检索.
  37. Campbell, Howard E. (1970). The Structure of Arithmetic. Appleton-Century-Crofts. 第 83 页. ISBN 978-0-390-16895-5.
  38. Garavel, Hubert (2017). “On the Most Suitable Axiomatization of Signed Integers”. Post-proceedings of the 23rd International Workshop on Algebraic Development Techniques (WADT'2016). Lecture Notes in Computer Science. 第 10644 卷. Springer. 第 120–134 页. doi:10.1007/978-3-319-72044-9_9. ISBN 978-3-319-72043-2. 2018 年 1 月 26 日存档. 2018 年 1 月 25 日检索.

10. 资料来源

11. 外部链接


致读者： 小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此，我们请求广大读者热心打赏 ，使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损， 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款， 他们的付出帮助了 99% 的读者免费获取知识， 我们在此表示感谢。

                     

友情链接： 超理论坛　|　©小时科技 保留一切权利