负数（综述）

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章

　　 在数学中，负数是正实数的相反数。\(^\text{[1]}\) 等价地说，负数是小于零的实数。负数常用于表示损失或缺少的量。例如，所欠的债务可以看作一种负资产。如果某个量（如电子的电荷）可以具有两种相反的性质，那么人们可以（有时是任意地）将其中一种记为正，另一种记为负。负数还用于描述那些可以小于零的刻度值，例如摄氏温度和华氏温度的刻度。负数的算术运算规律保证了 “相反数” 的直观概念能够反映在运算中。例如：$-(-3) = 3$ 因为 “相反数的相反数” 就是原数本身。

　　 负数通常写作前面带一个负号。例如：$-3$ 表示一个大小为 3 的负量，读作 “负三” 或 “减三”。相反地，大于零的数称为正数；零通常（但并非总是）被认为既不是正数，也不是负数。\(^\text{[2]}\) 正数的性质有时会用加号来强调，例如：$+3$。一般而言，数的 “正负性” 被称为它的符号。

　　 除了零之外，每一个实数要么是正数，要么是负数。非负整数通常称为自然数（即 $0, 1, 2, 3, \ldots$），而正整数、负整数以及零合在一起称为整数。（有些自然数的定义并不包括零。）

　　 在簿记中，所欠的金额常用红色数字或括号中的数字表示，作为负数的一种替代记号。负数早在中国汉代（公元前 202 年 – 公元 220 年）成书的《九章算术》中就已使用，不过其中可能包含更古老的材料。\(^\text{[3]}\) 大约三世纪的数学家刘徽建立了负数加减的运算规则。\(^\text{[4]}\) 到七世纪，印度数学家如婆罗摩笈多已经在描述负数的运用。伊斯兰数学家进一步发展了负数的减法与乘法规则，并解决了带有负系数的问题。\(^\text{[5]}\) 在负数概念出现之前，像丢番图这样的数学家认为负解是 “错误的”，并称要求负解的方程为荒谬的。\(^\text{[6]}\) 西方数学家如莱布尼茨曾坚持认为负数是无效的，但在计算中仍然使用它们。\(^\text{[7][8]}\)

1. 引言

数轴

　　 负数、正数与零之间的关系通常用数轴的形式来表示：

　　 数轴上越靠右的数值越大，而越靠左的数值越小。因此，零位于中间，右边是正数，左边是负数。

　　 需要注意的是，绝对值更大的负数被认为更小。例如，尽管正数 8 大于正数 5，写作： $$ 8 > 5~ $$ 但负数 8 被认为小于负数 5： $$ -8 < -5~ $$

带符号的数

　　 在负数的语境下，大于零的数称为正数。因此，除了零以外的每个实数要么是正的，要么是负的，而零本身被认为没有符号。正数有时会在前面加上一个加号，例如：$+3$ 表示正三。

　　 由于零既不是正数，也不是负数，因此有时会使用非负来指代大于或等于零的数，而用非正来指代小于或等于零的数。零是一个中性数。

作为减法的结果

　　 负数可以被看作是小数减大数的结果。例如，负三就是从零减去三得到的： $$ 0 - 3 = -3~ $$ 一般来说，当一个较小的数减去一个较大的数时，结果是负数，并且其绝对值等于两数之差。 例如： $$ 5 - 8 = -3~ $$ 因为：$8 - 5 = 3$.

2. 负数的日常应用

体育

• 足球与冰球：用净胜球表示进球与失球的差值；
• 橄榄球：用净得分；
• 板球：用净得分率；
• 高尔夫：用相对于标准杆（par）的成绩来表示，低于标准杆为负分。
• 冰球的正负值统计：当某个球员在场时，球队的总进球（+）减去总失球（−）的差值就是该球员的+/− 评分。球员可能拥有一个负的 +/− 评分。
• 棒球的净得分差：如果球队的失分多于得分，则净得分差为负数。
• 体育俱乐部积分扣除：若违反规则，俱乐部可能被扣分，从而在赛季初始时出现负的积分，直到赢得足够的分数抵消为止。\(^\text{[9][10]}\)
• 一级方程式（F1）赛车：单圈或分段时间常以与前一圈（或分段）的差值表示（可能是纪录圈，或前车刚完成的圈速）。如果更慢，则为正差值；如果更快，则为负差值。\(^\text{[11]}\)
• 田径项目（如短跑、跨栏、三级跳远和跳远）：风速助力会被测量并记录，顺风为正值，逆风为负值。\(^\text{[12][13]}\)

科学

• 温度：低于 $0 \,^\circ\text{C}$ 或 $0 \,^\circ\text{F}$ 的温度。\(^\text{[14][15]}\)
• 地理坐标：赤道以南的纬度、以及本初子午线以西的经度记作负数。
• 地形高度：地球表面的地形通常以海平面为基准来表示高度，可以是负值（例如：死海、死亡谷的地表高度，或泰晤士潮汐隧道的高度）。
• 电路：当电池反向连接时，所加电压与其额定电压相反。例如，一个 6 伏电池若反向连接，则施加电压为 $-6$ 伏。
• 离子：可以带正电或负电。

金融

• 财务报表：可以包含负余额，用负号或用括号标示。例如：银行账户透支、企业亏损（负收益）。\(^\text{[17]}\)
• GDP 增长率：一国国内生产总值的年增长率可能为负，这是经济衰退的一个指标。\(^\text{[17]}\)
• 通货紧缩：在少数情况下，通货膨胀率可能为负（即通货紧缩），表示物价总体下降。\(^\text{[18]}\)
• 股票与指数：如富时 100 指数、道琼斯指数，其日变动可能为负。
• 融资中的负数：负数通常与债务、赤字同义，也常被称为 “赤字状态”。
• 负利率：在某些情况下，存款人需要向银行支付费用。\(^\text{[19][20][21]}\)

其他

• 楼层编号：在建筑物中，地面以下的楼层常用负数编号。
• 音频播放器：在便携式媒体播放器（如 iPod）播放音频文件时，屏幕显示的剩余时间可能以负数形式出现，并且随着剩余时间趋近于零而增加，其速率与已播放时间自零开始增加的速率相同。
• 电视竞赛节目：
• 在《QI》节目中，参赛者常常以负分结束。
• 在《University Challenge》节目中，如果队伍抢答错误，则会被扣分，可能出现负分。
• 在《Jeopardy!》节目中，分数以金钱形式计，若错误回答导致损失大于现有分数，则会出现负数金额。
• 在《The Price Is Right》节目的 “Buy or Sell” 游戏中，如果损失金额超过当前账户中的金额，就会出现负分。
• 政治学：在大选之间，一个政党的支持率变化被称为摇摆，可以为负。
• 政治人物的支持率：支持率可能下降，从而显示为负的变化值。\(^\text{[22]}\)
• 电子游戏：根据模拟类型不同，负数可能表示失去生命、受到伤害、分数惩罚或资源消耗。
• 弹性工时制度：若员工累计工时少于合同要求，则其工时表可能显示为负工时余额。此外，员工在一年中可能休假超额，未用工时会形成负余额并结转到下一年。
• 电子键盘乐器：移调音符时，显示屏上用正数表示升高，用负数表示降低。例如：“−1” 表示下降一个半音。

3. 含负数的算术运算

　　 符号 “−” 既可以表示二元运算符（减法运算，例：$y - z$），也可以表示一元运算符（取负运算，例：$-x$，或两次出现如 $-(-x)$）。一元取负运算作用于正数时是一个特殊情况，此时结果为负数（如 $-5$）。

　　 虽然符号 “−” 的多重含义在形式上可能产生歧义，但在算术表达式中通常不会引起实际歧义，因为运算顺序规则决定了对每个 “−” 只有唯一的解释。然而，当运算符号彼此相邻出现时，可能会让人困惑或难以理解。一种解决办法是用括号将一元负号与其操作数括起来。

　　 例如，表达式：$7 + -5$ 写作：$7 + (-5)$ 可能更清晰（尽管两者在形式上完全等价）。而减法表达式：$7 - 5$ 则是不同的运算，尽管其结果相同。在小学教育中，有时会在数的前面加上上标的正负号，以明确区分正数与负数，例如： $$ -2 + -5 = -7~ $$

加法

　　 两个负数的加法与两个正数的加法非常相似。例如： $$ (-3) + (-5) = -8~ $$ 这里的思想是：两笔债务可以合并为一笔更大的债务。

　　 当正数与负数混合相加时，可以把负数看作是要被减去的正数。例如： $$ 8 + (-3) = 8 - 3 = 5~ $$ 和 $$ (-2) + 7 = 7 - 2 = 5~ $$ 在第一个例子中，8 的 “资产” 与 3 的 “债务” 相加，结果是 5 的净资产。

　　 如果负数的绝对值更大，结果就为负数： $$ (-8) + 3 = 3 - 8 = -5~ $$ 和 $$ 2 + (-7) = 2 - 7 = -5~ $$ 在这里，资产小于债务，因此净结果是债务。

减法

　　 如前所述，两个非负数相减可能会得到一个负数： $$ 5 - 8 = -3~ $$ 一般来说，减去一个正数等价于加上一个相同大小的负数。因此： $$ 5 - 8 = 5 + (-8) = -3~ $$ 以及： $$ (-3) - 5 = (-3) + (-5) = -8~ $$ 另一方面，减去一个负数等价于加上一个相同大小的正数。（其思想是：失去一笔债务等同于获得一笔资产。）因此： $$ 3 - (-5) = 3 + 5 = 8~ $$ 以及： $$ (-5) - (-8) = (-5) + 8 = 3~ $$

乘法

　　 在数的乘法中，积的大小总是等于两个数的绝对值的乘积。积的符号则由以下规则决定：

• 一个正数与一个负数的积是负数；
• 两个负数的积是正数。

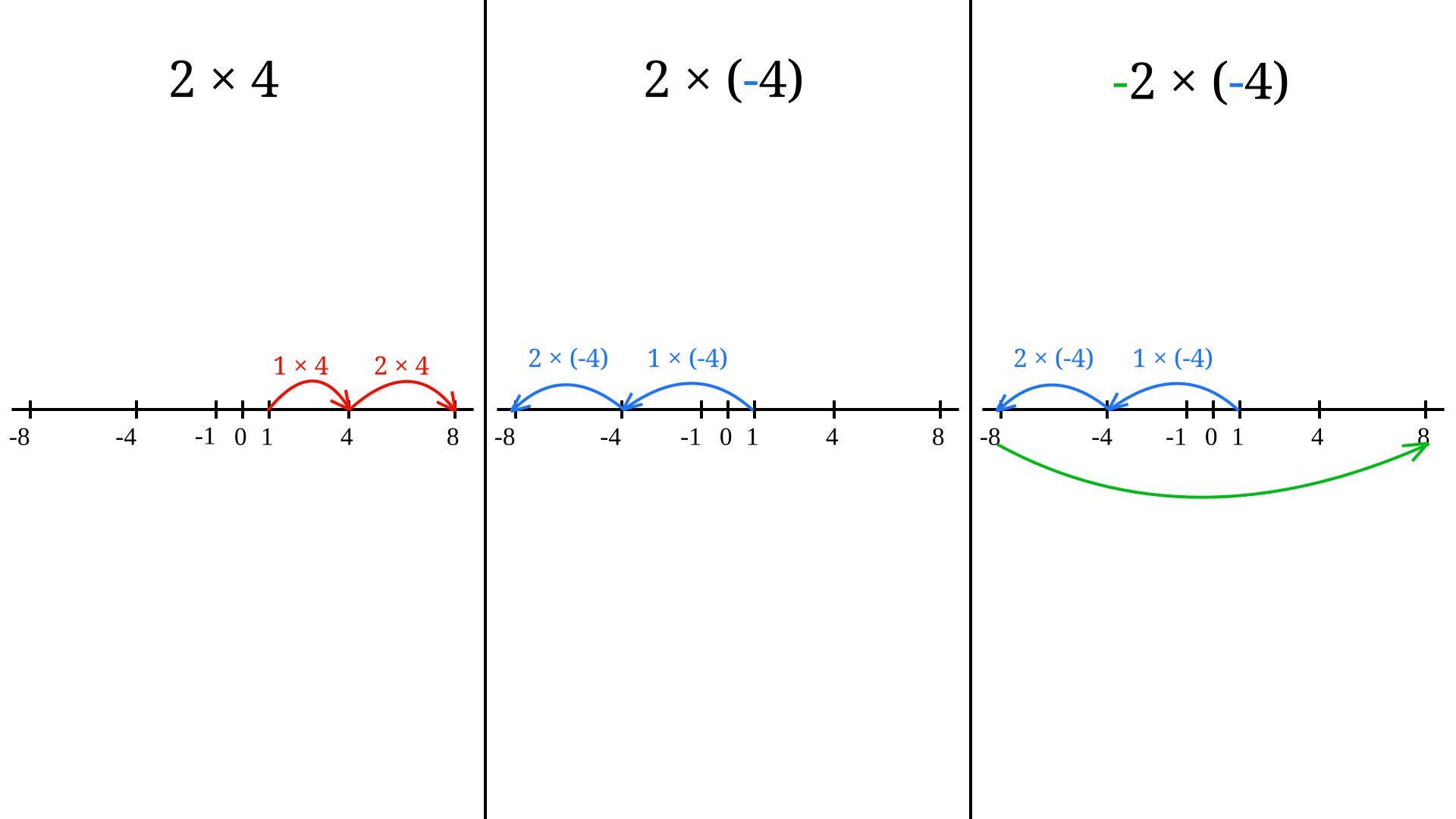
　　 因此： $$ (-2) \times 3 = -6~ $$ 以及： $$ (-2) \times (-3) = 6~ $$ 第一个例子的原因很简单：把三个 $-2$ 相加等于 $-6$： $$ (-2) \times 3 = (-2) + (-2) + (-2) = -6~ $$ 第二个例子的推理更复杂一些。其思想仍然是 “失去一笔债务等于获得一笔资产”。在这里，失去两笔每笔 3 的债务，等价于获得 6 的资产： $$ (-2 \,\text{debts}) \times (-3 \,\text{each}) = +6 \,\text{credit}~ $$ 规定 “两负相乘得正” 不仅有直观解释，也是为了保证乘法遵循分配律。 例如： $$ (-2) \times (-3) + 2 \times (-3) = (-2 + 2) \times (-3) = 0 \times (-3) = 0~ $$ 由于：$2 \times (-3) = -6$ 因此，为了等式成立，必须有：$(-2) \times (-3) = 6$.

　　 这些规则导出另一个（等价的）规则——积 $a \times b$ 的符号取决于 $a$ 的符号，如下：

• 如果 $a$ 是正数，那么 $a \times b$ 的符号与 $b$ 的符号相同；
• 如果 $a$ 是负数，那么 $a \times b$ 的符号与 $b$ 的符号相反。

　　 关于为什么两个负数的积是正数的解释，可以在复数分析中得到说明。

除法

　　 除法的符号规则与乘法相同。例如： $$ 8 \boldsymbol{\nabla}\boldsymbol{\cdot} (-2) = -4,~ $$ $$ (-8) \boldsymbol{\nabla}\boldsymbol{\cdot} 2 = -4,~ $$ 以及： $$ (-8) \boldsymbol{\nabla}\boldsymbol{\cdot} (-2) = 4~ $$ 如果被除数和除数符号相同，则结果为正；如果它们符号不同，则结果为负。

4. 取负

　　 一个正数的负数形式称为它的取负。例如，$-3$ 是正数 3 的取负。一个数与其取负数的和等于零： $$ 3 + (-3) = 0~ $$ 也就是说，正数的取负就是该数的加法逆元。

　　 利用代数，可以将这一原理写为一个恒等式： $$ x + (-x) = 0~ $$ 这个恒等式对任何正数 $x$ 都成立。 如果将 “取负” 的定义扩展到零和负数，那么它对所有实数都成立。具体来说：

• 0 的取负是 0；
• 一个负数的取负是对应的正数。

　　 例如：$-3$ 的取负是 $+3$。一般而言： $$ -(-x) = x~ $$ 一个数的绝对值是与它大小相同的非负数。例如，$-3$ 的绝对值和 $3$ 的绝对值都等于 3，而 $0$ 的绝对值是 0。

5. 负整数的形式化构造

　　 类似于有理数的构造方式，我们可以将自然数 $\mathbb{N}$ 扩展为整数 $\mathbb{Z}$ 方法是：把整数定义为自然数的有序对 $(a, b)$。加法与乘法可以扩展到这些有序对，规则如下： $$ (a, b) + (c, d) = (a + c, b + d)~ $$ $$ (a, b) \times (c, d) = (a \times c + b \times d, \; a \times d + b \times c)~ $$ 我们在这些有序对上定义一个等价关系 $\sim$，规则如下： $$ (a, b) \sim (c, d) \quad \text{当且仅当 } a + d = b + c~ $$ 这个等价关系与上述的加法和乘法相容，因此我们可以定义：$\mathbb{Z} = \mathbb{N}^2 / \sim$ 也就是说，如果两个有序对在上述意义下等价，我们就将它们识别为同一个整数。注意：配备了这种加法与乘法运算的 $\mathbb{Z}$ 构成一个环（ring），而且事实上它是环的原型例子。

　　 我们还可以在 $\mathbb{Z}$ 上定义一个全序： $$ (a, b) \leq (c, d) \quad \text{当且仅当 } a + d \leq b + c~ $$ 由此可以得到：加法零元：形如 $(a, a)$；加法逆元：$(a, b)$ 的加法逆元是 $(b, a)$；乘法单位元：形如 $(a+1, a)$；减法定义为： $$ (a, b) - (c, d) = (a + d, b + c)~ $$ 这种构造是格罗滕迪克构造的一个特例。

唯一性

　　 一个数的加法逆元是唯一的，证明如下。如前所述，一个数的加法逆元定义为：当它与该数相加时，结果为零。

　　 设 $x$ 是一个数，$y$ 是它的加法逆元。假设 $y'$ 是 $x$ 的另一个加法逆元。根据定义： $$ x + y' = 0, \quad \text{并且} \quad x + y = 0~ $$ 因此：$x + y' = x + y$ 根据加法的消去律，可以得到：$y' = y$ 于是 $y$ 等于任何其它可能的加法逆元。也就是说，$y$ 是 $x$ 的唯一加法逆元。

6. 历史

　　 长期以来，人们对负数的理解受阻，原因在于无法想象具有负数量的实物，例如 “负三只苹果”；因此，方程的负解常被认为是 “错误的”。

　　 在希腊化时期的埃及，公元 3 世纪的希腊数学家丢番图在其著作 Arithmetica 中提到过一个等价于 $4x + 20 = 4$（其解为负数）的方程，并称该方程为荒谬的。\(^\text{[24]}\) 因此，希腊几何学家只能在几何上解决那些给出正根的二次方程形式，而对其他情况则无法处理。\(^\text{[25]}\)

　　 负数在历史上首次出现于《九章算术》（Jiǔ zhāng suàn-shù, 九章算術）。这部著作在现存形式上可追溯到汉代，但其中很可能包含更早的材料。\(^\text{[3]}\) 数学家刘徽（约公元 3 世纪）建立了负数加减的规则。历史学家 Jean-Claude Martzloff 推测，中国自然哲学中 “阴阳对立” 的重要性，使得中国人更容易接受负数的概念。\(^\text{[4]}\) 中国数学家能够解涉及负数的联立方程。《九章算术》中使用红色算筹表示正系数，黑色算筹表示负系数。\(^\text{[4][26]}\) 这种方法恰好与现代银行、会计和商业领域中正负数的印刷习惯相反：现代记法里，红色数字表示负值，黑色数字表示正值。刘徽写道：

　　 “今有正负二算以辨盈虚，谓之正负。赤算者正，黑算者负。”\(^\text{[4]}\)

　　 古印度的《婆什迦罗手稿》已经包含了负数运算，并且使用 “+” 作为负号。\(^\text{[27]}\) 该手稿的年代尚不确定：L.V. Gurjar 认为其不晚于 4 世纪，\(^\text{[28]}\)Hoernle 认为介于 3 至 4 世纪之间，Ayyangar 和 Pingree 认为是 8 至 9 世纪，\(^\text{[29]}\) 而 George Gheverghese Joseph 则推测大约写于公元 400 年，不晚于 7 世纪初。\(^\text{[30]}\)

　　 到公元 7 世纪，印度已使用负数来表示债务。印度数学家婆罗摩笈多在其著作《婆罗摩-苏普塔-悉檀多》（Brahma-Sphuta-Siddhanta, 公元约 630 年）中讨论了负数的运用，并给出了类似于今天所用的二次方程通用公式。\(^\text{[24]}\)

　　 在 9 世纪，伊斯兰数学家通过研读印度数学著作而接触到负数，但在这一时期对负数的承认和使用仍显谨慎。\(^\text{[5]}\) 例如，花剌子密在其《代数学书》（“algebra” 一词即源于此书名）中，并未使用负数或负系数。\(^\text{[5]}\) 然而，在此之后不到五十年，阿布·卡米勒就已经阐述了符号法则，并用于展开：$(a \pm b)(c \pm d)$\(^\text{[31]}\) 同时，卡拉吉在其《法赫里书》中写道：“负量必须被视为项”。\(^\text{[5]}\) 到了 10 世纪，阿布·瓦法·布兹贾尼在其著作《书记与商人算术学中必要之书》中，已将债务视为负数。\(^\text{[31]}\)

　　 到 12 世纪，卡拉吉的继承者们已经提出了符号的一般法则，并将其用于解决多项式除法。\(^\text{[5]}\) 正如萨马瓦尔所写：

　　 “负数（al-nāqiṣ，意为亏损）乘以正数（al-zāʾid，意为收益），结果为负；负数乘以负数，结果为正。如果用一个较大的负数减去一个较小的负数，余数是它们的负差。如果用一个较小的负数减去一个较大的负数，差则为正。如果用正数减去负数，余数是它们的正和。如果从一个空次幂中减去正数，余数是同样的负数；如果从一个空次幂中减去负数，余数是同样的正数。”\(^\text{[5]}\)

　　 在 12 世纪印度，数学家婆什迦罗二世给出了二次方程的负根，但因在问题语境下 “不合适” 而予以舍弃。他指出，负值 “在这种情况下不应采纳，因为它是不恰当的；人们不赞同负根”。

　　 斐波那契在《算盘书》（Liber Abaci，1202 年）中，允许在金融问题中出现负解，并将其解释为负债；在其后著作《花》（Flos，1225 年）中，又将其解释为亏损。

　　 在 15 世纪，法国人 Nicolas Chuquet 使用了负数作为指数 \(^\text{[32]}\)，但称它们为 “荒谬数”。\(^\text{[33]}\)

　　 Michael Stifel 在其 1544 年的著作《整数算术》中讨论了负数，并同样称其 numeri absurdi（荒谬数）。

　　 到 1545 年，吉罗拉莫·卡尔丹诺（在其著作《大术》（Ars Magna）中，首次在欧洲对负数作出了令人满意的处理。\(^\text{[24]}\) 不过，他在处理三次方程时仍然不允许出现负数，因此不得不将以下两类方程分开讨论：$x^{3} + ax = b$ 与 $x^{3} = ax + b$（其中 $a, b > 0$）。总的来说，卡尔丹诺不得不研究 13 种类型的三次方程，并将所有负项移到等号另一边，使其变为正数。（卡尔丹诺也讨论过复数，但他显然对其接受程度更低。）

7. 参见

• 带符号的零
• 加法逆元
• 零的历史
• 整数
• 正负部分
• 有理数
• 实数
• 符号函数
• 符号（数学）
• 带符号数表示法

8. 参考文献

引文

1. “整数是整数及其相反数的集合。”——Richard W. Fisher, No-Nonsense Algebra, 2nd Edition, Math Essentials, ISBN 978-0999443330
2. 关于零既非正也非负的约定并非普遍存在。例如，在法国的约定中，零既被视为正数，也被视为负数。法语单词 positif 与 négatif 分别等同于英语的 “positive or zero” 与 “negative or zero”。
3. Struik，第 32–33 页：“在这些矩阵中我们发现了负数，它们首次在历史中出现。”
4. Hodgkin, Luke (2005). A History of Mathematics: From Mesopotamia to Modernity. 牛津大学出版社. 第 88 页. ISBN 978-0-19-152383-0. ——刘徽在这里表述得很明确：在《九章算术》详细阐述的 “正负法则” 处。
5. Rashed, R. (1994 年 6 月 30 日). The Development of Arabic Mathematics: Between Arithmetic and Algebra. 施普林格出版社. 第 36–37 页. ISBN 9780792325659.
6. 丢番图, Arithmetica.
7. Kline, Morris (1972). Mathematical Thought from Ancient to Modern Times. 纽约：牛津大学出版社. 第 252 页。
8. Smith, Martha K. (2001 年 2 月 19 日). “History of Negative Numbers”. 德克萨斯大学. 原文存档于 2025 年 2 月 27 日。
9. “Saracens 薪资上限违规：英超冠军不会对处罚提出异议”。BBC Sport. 检索于 2019 年 11 月 18 日。——Mark McCall 的球队因此从英超积分榜第三降至垫底，积分为 −22。
10. “Bolton Wanderers 1−0 Milton Keynes Dons”. BBC Sport. 检索于 2019 年 11 月 30 日。——在补时第 3 分钟，这名前锋将 Luke Murphy 的传中在 8 码处射入，帮助 Hill 的球队取得英甲三连胜。他们在赛季初因破产清算而被扣除 −12 分。
11. “术语表”。Formula1.com. 检索于 2019 年 11 月 30 日。——Delta time（时间差）：用于描述两圈成绩或两辆车之间的时间差。例如，车手的最佳练习圈与最佳排位圈之间通常存在负的 delta，因为排位圈时油量更少并且使用新轮胎。
12. “BBC Sport - 奥运会 - 伦敦 2012 - 男子跳远：田径 - 成绩”。2012 年 8 月 5 日。存档于 2012 年 8 月 5 日。检索于 2018 年 12 月 5 日。
13. “田径中的风助原理（How Wind Assistance Works in Track & Field）”。elitefeet.com. 2008 年 7 月 3 日。检索于 2019 年 11 月 18 日。——风助通常以米/秒表示，可以是正数或负数。正值表示顺风帮助运动员，负值表示运动员顶风而跑。例如：风速 −2.2 m/s 和 +1.9 m/s 被视为合规，而 +2.1 m/s 的风速则风助过大，判定为违规。常用术语还包括 “顺风”（+，推动运动员向前）和 “逆风”（−，抵消运动员速度）。
14. Forbes, Robert B. (1975 年 1 月 6 日). 《白令海盆地及邻近区域地质研究：收录自白令海区域地质与地球物理研讨会（1970 年 6 月 26–28 日，阿拉斯加大学 C.T. Elvey 大楼启用仪式期间）及第二届北极地质国际研讨会（1971 年 2 月 1–4 日，旧金山）》。美国地质学会。第 194 页。ISBN 9780813721514。
15. Wilks, Daniel S. (2018 年 1 月 6 日). 《大气科学中的统计方法》.Academic Press. 第 17 页. ISBN 9780123850225.
16. Carysforth, Carol; Neild, Mike (2002). Double Award. Heinemann. 第 375 页. ISBN 978-0-435-44746-5.
17. “英国经济在 2012 年底萎缩”。BBC 新闻. 2013 年 1 月 25 日. 检索于 2018 年 12 月 5 日。
18. “自 1960 年以来的首个负通胀数据”。《独立报》. 2009 年 4 月 21 日. 2022 年 6 月 18 日存档. 检索于 2018 年 12 月 5 日。
19. “欧洲央行实施负利率”。BBC 新闻. 2014 年 6 月 5 日. 检索于 2018 年 12 月 5 日。
20. Lynn, Matthew. “认为负利率不可能发生在这里？再想想吧”。MarketWatch. 检索于 2018 年 12 月 5 日。
21. “瑞士利率将转为负值”。BBC 新闻. 2014 年 12 月 18 日. 检索于 2018 年 12 月 5 日。
22. Wintour, Patrick (2014 年 6 月 17 日). “米利班德和克莱格的支持率降至 ICM 民调记录的最低水平”。《卫报》. 检索于 2018 年 12 月 5 日 – 来源：[www.theguardian.com。](http://www.theguardian.com。)
23. Grant P. Wiggins; Jay McTighe (2005). 《以理解为目标的课程设计》. ACSD Publications. 第 210 页. ISBN 1-4166-0035-3.
24. Needham, Joseph; Wang, Ling (1995) [1959]. 《中国科学技术史：第三卷；数学与天文地学》（Science and Civilisation in China: Volume 3; Mathematics and the Sciences of the Heavens and the Earth, 重印版）. 剑桥：剑桥大学出版社. 第 90 页. ISBN 0-521-05801-5.
25. Heath, Thomas L. (1897). 《阿基米德全集》. 剑桥大学出版社. 第 cxxiii 页.
26. Needham, Joseph; Wang, Ling (1995) [1959]. 《中国科学技术史：第三卷；数学与天文地学》（Science and Civilisation in China: Volume 3; Mathematics and the Sciences of the Heavens and the Earth, 重印版）. 剑桥：剑桥大学出版社. 第 90–91 页. ISBN 0-521-05801-5.
27. Teresi, Dick (2002). 《失落的发现：现代科学的古代根源——从巴比伦人到玛雅人》. 纽约：西蒙与舒斯特出版社. ISBN 0-684-83718-8. 第 65 页。
28. Pearce, Ian (2002 年 5 月). “《婆什迦罗手稿》”. MacTutor 数学史档案. 检索于 2007 年 7 月 24 日。
29. Hayashi, Takao (2008). “Bakhshālī Manuscript”, 收录于 Helaine Selin (编), 《非西方文化中的科学、技术与医学史百科全书》, 第一卷, 施普林格出版社. 第 B2 页. ISBN 9781402045592.
30. Teresi, Dick (2002). 《失落的发现：现代科学的古代根源——从巴比伦人到玛雅人》. 纽约：西蒙与舒斯特出版社. ISBN 0-684-83718-8. 第 65–66 页。
31. Bn Ismail, Mat Rofa (2008). “Algebra in Islamic Mathematics”, 收录于 Helaine Selin (编), 《非西方文化中的科学、技术与医学史百科全书》（第 2 版）, 第一卷, 施普林格出版社. 第 115 页. ISBN 9781402045592.
32. Flegg, Graham; Hay, C.; Moss, B. (1985). 《尼古拉·舒凯：文艺复兴时期的数学家——含舒凯 1484 年数学手稿的大量译文研究》. D. Reidel Publishing Co. 第 354 页. ISBN 9789027718723.
33. Johnson, Art (1999). 《著名难题及其数学家》（Famous Problems and Their Mathematicians）. Greenwood Publishing Group. 第 56 页. ISBN 9781563084461.

参考书目

• Bourbaki, Nicolas (1998). 《数学史纲要》. 柏林、海德堡、纽约：施普林格出版社. ISBN 3-540-64767-8.
• Struik, Dirk J. (1987). 《数学简史》. 纽约：Dover 出版社.

9. 外部链接

• Maseres 的传记信息
• BBC Radio 4 系列节目 In Our Time——2006 年 3 月 9 日播出主题《负数》。
• 无尽的例题与练习：带符号整数的运算
• 数学论坛：Ask Dr. Math 常见问题——负数乘负数