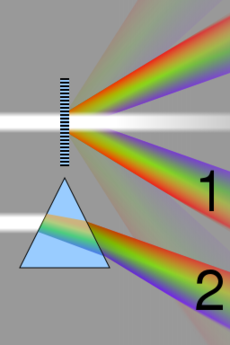
衍射光栅

贡献者： 待更新

　　 （本文根据 CC-BY-SA 协议转载自原搜狗科学百科对英文维基百科的翻译）

　　 在光学中，衍射光栅是一种具有周期性结构的光学元件，它将光分裂并衍射成沿不同方向传播的几束光束。它形成的着色是一种具有结构性的着色。[1][2] 这些光束的方向取决于光栅的间距和光的波长，因此光栅充当色散元件。由于这些原因，光栅通常用于制作单色仪和光谱仪。

　　 在实际应用中，光栅通常在其表面有脊或划线，而不是暗线。这种光栅可以是透射型的，也可以是反射型的。除了振幅调制型光栅以外，也可以制备出相位调制型的光栅。这种光栅通常采用全息法制备[3]

　　 衍射光栅的原理是詹姆斯·格雷戈里在牛顿棱镜实验大约一年后发现的，最初是用鸟类羽毛等物品作为光栅。[4] 第一个人造衍射光栅是费城发明家大卫·黎顿郝斯在 1785 年左右制造的，他把头发串在两个细螺丝之间。[5][6] 这类似于 1821 年著名的德国物理学家约瑟夫·冯·夫琅和费的线衍射光栅。[7][8] 19 世纪 60 年代，格里弗斯瓦尔德的弗里德里希·阿道夫·诺贝特（1806-1881）创造了线距 d 最小的光栅，[9] 随后两位美国人路易斯·莫里斯·拉瑟弗德（1816-1892）和威廉·罗杰斯（1804-1882）占据了领先地位，[10][11] 到 19 世纪末，亨利·奥古斯谭斯·罗兰（1848-1901）的凹面光栅成为了现有的最佳光栅[12][13]。

　　 当被宽光谱（例如连续谱）光源照射时，衍射可以产生 “彩虹” 色。光存储磁盘（如光盘或数字视盘）上紧密间隔的窄轨道产生的闪光效应就是一个例子，而薄层油（或汽油等）产生的类似彩虹效应则不是由光栅引起的，而是由具有紧密间隔的透射层中由于反射导致的干涉效应引起的（参见下面的例子）。光栅有平行线，而光盘有一个螺旋的精细间隔的数据轨道。当透过半透明的细间距伞状织物覆盖物观察亮点光源时，也会出现衍射色。基于反射光栅片的装饰性图案塑料薄膜非常便宜，并且很常见。

1. 工作原理

　　 光栅间距与入射光束和衍射光束的角度之间的关系称为光栅方程。

　　 根据惠更斯-菲涅尔原理，传播波波前上的每个点都可以被认为是一个点源，通过将这些单独点源的贡献相加，可以找到任何后续点的波前。

　　 光栅可以是 “反射” 或 “透射” 型的，分别类似于镜子或透镜。光栅具有 “零阶模式”（其中 m = 0），在这种模式下没有衍射。光线的行为根据反射和折射定律分别与镜子或透镜相同。

　　 理想光栅由一组间距为 d 的狭缝组成，光栅间距必须比关注的波长更宽才能引起衍射。假设一束波长为λ的单色平面波正入射（垂直于光栅）到光栅上，光栅中的每个狭缝充当准点光源，光从该准点光源向所有方向传播（尽管这通常限于半球面）。光与光栅相互作用后，衍射光由光栅中每个狭缝发出的干涉波分量之和组成。在衍射光可以通过的任何给定空间点，光栅中每个狭缝的路径长度都是不同的。因为路径长度通常是不同的，所以每个狭缝在该点的波的相位也是不同的。因此，它们相互加减，通过干涉相长或干涉相消产生透射峰和透射谷。当来自相邻狭缝的光之间的路径差等于波长的一半（λ2）时，波是异相的，因此彼此抵消以产生最小强度的点。类似地，当路径差为λ时，相位相加，光强出现最大值。最大值出现在满足关系式 d sinθmλ = | m |的角度θm 处，其中θm 是衍射光线和光栅法向矢量之间的角度，d 是从一个狭缝中心到相邻狭缝中心的距离，m 是表示关注的传播模式的阶数。

　　 因此，当光正入射到光栅上时，衍射光强在角度θm 处具有最大值，由下式给出:

　　 $$ d \sin \theta_m = m \lambda~$$.

　　 显而易见，如果平面波以任意角度 $\theta_i$ 入射，光栅方程变为：

　　 $$d (\sin \theta_i - \sin \theta_m) = m \lambda~$$.

　　 当求解第 $m$ 级的衍射角时，方程为：

　　 $$\theta_m = \arcsin \left( \sin \theta_i - \frac{m \lambda}{d} \right)~$$.

　　 请注意，这些方程假设光栅的两侧与同种介质（例如空气）接触。对应于直接透射（或反射光栅情况下的镜面反射）的光称为零阶衍射光，表示成 m = 0。其他光强最大值出现在由非零整数 m 表示的角度。注意，m 可以是正的或负的，对应于零级光束两侧的衍射级。

　　 上述光栅方程的推导是基于理想光栅。然而，衍射光束的角度、光栅间距和光波长之间的关系适用于间距相同的任何规则结构，因为从光栅的相邻基本单元散射的光之间的相位关系保持不变。衍射光的具体分布取决于光栅基本单元的具体结构以及光栅中基本单元的数量，但是它总是在光栅方程给出的方向上给出光强最大值。

　　 光栅可以通过周期性地调制入射光的各种特性来制成，包括：

• 透过率（透射振幅衍射光栅）；
• 反射率（反射振幅衍射光栅）；
• 折射率或光程长度（相位衍射光栅）；
• 光轴方向（光轴衍射光栅）。

　　 光栅方程适用于所有以上这些情况。

1.1 量子电动力学

　　 量子电动力学（QED）以光子作为粒子（在某种程度上）提供了衍射光栅性质的另一种推导。量子电动力学可以用量子力学的路径积分公式直观地描述。因此，它可以将光子建模为潜在地沿着从源到最终点的所有路径，每条路径都具有一定的概率幅度。这些概率幅度可以用复数或等价向量来表示——或者，正如理查德·费曼在他关于量子电动力学的书中简单地称之为 “箭头”。

　　 对于某个事件发生的概率，我们将事件所有可能发生方式的概率振幅相加，然后取其模的平方。在这种情况下，来自单色光源的光子在给定时间到达某个最终点的概率幅度可以被建模为快速旋转的箭头，直到光子到达其最终点时才被评估。例如，对于光子从镜子反射并在给定时间后在给定点被观察的概率，可以设置光子离开光源时旋转的概率幅度，跟随它到达镜子，然后到达它的最终点，即使对于不涉及以相等角度从镜子反射的路径也是如此。然后，可以评估光子最终点的概率振幅；接下来，可以对所有这些箭头进行积分（见矢量和），并对积分结果的模求平方，以获得光子以相干的方式从反射镜反射出去的概率。这些路径所花费的时间决定了概率振幅箭头的角度，因为它们可以说是以恒定的速率 “旋转”（这与光子的频率有关）。

　　 镜子经典反射点附近路径的时间几乎相同，因此概率振幅几乎指向相同的方向——因此，它们的总和相当大。观察朝向镜子边缘的路径可以发现，附近路径的时间彼此相差很大，因此我们得出的矢量总和会很快抵消掉。因此，与更远的路径相比，光更有可能遵循接近经典的反射路径。然而，衍射光栅可以由这种反射镜制成，通过去除反射镜边缘附近通常会抵消附近振幅的区域——但是现在，由于光子不会从被去除的部分反射，所有指向的概率振幅，例如 45 度，可以有一个相当大的总和。因此，这使得合适频率的光累加成更大的概率幅度，因此具有更大的概率到达适当的最终点。

　　 这个特殊的描述包括许多简化：点光源，一个可以反射光的 “表面”（因此和电子的相互作用被忽略），等等。最大的简化可能在于概率振幅箭头的 “旋转” 实际上被更准确地解释为源的 “旋转”，因为光子在传输过程中的概率振幅不 “旋转”。我们通过让光子离开光源的时间变得不确定来获得概率振幅的相同变化——路径的时间现在告诉我们光子什么时候离开光源，它的 “箭头” 的角度是多少。然而，这种模型和近似物是从概念上说明衍射光栅的合理模型。不同频率的光也可以从相同的衍射光栅反射，但是具有不同的最终点。[14]

2. 光栅作为色散元件

　　 光栅方程中的波长依赖性表明，光栅将入射的多色光束分解成具有不同波长的光分量，即发生色散。输入光束中具有不同波长的光被衍射到不同的方向，在白光照明下产生彩虹色。这在视觉上类似于棱镜的作用，尽管其机制非常不同。

　　 根据入射光束的光谱的成分和光栅密度，对应于连续级的衍射光束可以重叠。光谱阶数越高，下一阶的重叠越大。

　　 光栅方程表明衍射级的角度只取决于凹槽的周期，而不取决于它们的形状。通过控制凹槽的横截面轮廓，对于给定的波长，可以以特定的顺序集中大部分衍射能量。通常使用三角形轮廓。这种技术被称为闪耀。衍射效率最高的入射角和波长通常称为闪耀角和闪耀波长。光栅的效率也可能取决于入射光的偏振。光栅通常由它们的凹槽密度来表示，每单位长度的凹槽数量，通常用每毫米的凹槽数（g/mm）来表示，也等于凹槽周期的倒数。凹槽周期必须和关注的波长在同一个数量级上；光栅覆盖的光谱范围取决于凹槽间距，并且对于具有相同光栅常数的直纹光栅和全息光栅是相同的。光栅可以衍射的最大波长等于光栅周期的两倍，这时入射光和衍射光与光栅法线成 90 度角。为了在更宽的频率上获得频率色散，必须使用棱镜。在光栅使用最普遍的光学系统中，这对应于 100 纳米和 10 微米之间的波长。在这种情况下，凹槽密度可以从每毫米几十个凹槽变化到每毫米几千个凹槽，如中阶梯光栅。

　　 当凹槽间距小于光波长的一半时，唯一存在的阶数是 m = 0 阶。具有如此小周期性的光栅被称为亚波长光栅，并表现出特殊的光学特性。由各向同性材料制成的亚波长光栅产生双折射，这种材料的表现就像是双折射的。

3. 制造

　　 最初，高分辨率光栅是使用高质量的划线机来刻划的，这些划线机的构建是一项大工程。亨利·约瑟夫·格雷森设计了一台制造衍射光栅的机器，成功地获得了每英寸 120，000 条线中的一条（大约每毫米 4，724 条线）。后来，光刻技术用全息干涉图案制作光栅。全息光栅具有正弦凹槽，可能不如直纹光栅有效，但在单色仪中通常是首选的，因为它们产生的杂散光较少。复制技术可以从任一类型的主光栅制作高质量的复制品，从而降低制造成本。

　　 制造衍射光栅的另一种方法是使用夹在两个衬底之间的光敏凝胶。后来人们发现通过全息干涉可以曝光凝胶。这些光栅，称为体积相位全息衍射光栅（或 VPH 衍射光栅），没有物理凹槽，而是凝胶内折射率的周期性调制。这在很大程度上消除了其他类型光栅中常见的表面散射效应。这些光栅也趋向于具有更高的效率，并且允许将复杂的图案包含到单个光栅中。在这种光栅的老版本中，环境敏感性是一种权衡，因为凝胶必须被控制在低温和低湿度下。通常，感光物质被密封在两个基底之间，使它们能够抵抗潮湿、热和机械应力。VPH 衍射光栅不会被意外触摸破坏，并且比典型的浮雕光栅更耐刮擦。

　　 现在，半导体技术也被用来将全息图案光栅蚀刻成坚固的材料，例如熔融石英。通过这种方式，可以将低杂散光全息术与深蚀刻透射光栅高效率地结合，并且可以进一步结合到大体积、低成本的半导体制造技术中。

　　 一种用于光栅插入到集成光子光波电路的新技术是数字平面全息术（DPH）。DPH 光栅模型在计算机中产生，并通过标准的微平版印刷术或纳米压印方法在光波导平面的一个或几个界面上制造，与大批量生产兼容。光在受折射率梯度限制的 DPH 光栅内传播，这提供了更长的相互作用路径和更大的操纵光的灵活性。

4. 例子

　　 衍射光栅通常用于单色仪、光谱仪、激光器、波分复用设备、光脉冲压缩设备和许多其他光学仪器。

　　 普通的压缩光盘和数字视盘介质是衍射光栅的常见例子，可以通过将太阳光反射到白色墙壁上来展示其效果。这是它们制造的副作用，因为光盘的一个表面在塑料中有许多小凹坑，排列成螺旋形；这个表面有一层薄薄的金属层，使凹坑更加清晰可见。光盘的结构在光学上是相似的，尽管它可能有不止一个具有凹痕的表面，并且所有具有凹痕的表面都在光盘内部。[15][16]

　　 由于对介质折射率的敏感性，衍射光栅可以用作流体性质的传感器。[17]

　　 当从垂直于凹槽的小角度观察时，在标准压制乙烯基唱片中，可以看到与光盘/数字视盘中相似但不太清晰的效果。这是由于视角（小于黑色乙烯基的临界角）和光被凹槽改变而反射的路径，产生了一个彩虹浮雕图案。

　　 衍射光栅还用于电子阅读器的具有均匀光强的前光，如背光电纸书（Nook Simple Touch with GlowLight）。[18]

4.1 电子元件光栅

　　 一些日常电子元件包含精细和规则的图案，因此很容易用作衍射光栅。例如，废弃手机和相机中的电荷耦合器件传感器可以从设备中移除。利用激光笔，衍射特性可以揭示出电荷耦合器件传感器的空间结构。[19] 这也可以用于智能手机的液晶显示器或发光二极管显示器。因为这种显示器通常仅由透明外壳保护，所以可以在不损坏手机的情况下进行实验。如果不打算进行精确测量，聚光灯可以显示出衍射图案。

4.2 自然光栅

　　 横纹肌是最常见的自然衍射光栅，[20] 有助于生理学家确定这种肌肉的内部结构。除此之外，晶体的化学结构可以被认为是除可见光以外的电磁辐射类型的衍射光栅，这是诸如 X 光晶体学等技术的基础。

　　 最常与衍射光栅混淆的是孔雀羽毛、珍珠母和蝴蝶翅膀的彩虹色。鸟类、[21] 鱼类[22] 和昆虫[21][23] 的彩虹色通常是由薄膜干涉而不是光栅衍射引起的。随着视角的变化，衍射产生宽的光谱，而薄膜干涉通常产生更窄的光谱范围。花的表面也可以产生衍射，但是植物的细胞结构通常太不规则，不能产生衍射光栅所需的精细狭缝的形状。[24] 因此，花的虹彩信号只能在非常局部的地方感知到，因此人类和访花昆虫看不到。[25][26] 然而，在一些无脊椎动物身上确实存在天然光栅，如孔雀蜘蛛[27]种虾的触角，甚至在伯吉斯页岩化石中也发现了天然光栅。[28][29]

　　 衍射光栅效应有时在气象学中可以看到。衍射冠状云是围绕光源（例如太阳）的彩色环。它们通常比光晕离光源更近，是由非常细小的粒子引起的，比如雾蒙蒙的天空中的水滴、冰晶或烟雾粒子。当粒子大小几乎相同时，它们以非常特定的角度衍射入射光。确切的角度值取决于粒子的大小。在雾中，衍射冠状云通常在光源周围观察到，如蜡烛火焰或路灯。云彩虹彩是由衍射引起的，尤其当云中的粒子大小一致时，一般沿着日冕环出现。[30]

5. 参考文献

　　 [1] ^Srinivasarao, M. (1999). "Nano-Optics in the Biological World: Beetles, Butterflies, Birds, and Moths". Chemical Reviews. 99 (7): 1935–1962. doi:10.1021/cr970080y. PMID 11849015..

　　 [2] ^Kinoshita, S.; Yoshioka, S.; Miyazaki, J. (2008). "Physics of structural colors". Reports on Progress in Physics. 71 (7): 076401. Bibcode:2008RPPh...71g6401K. doi:10.1088/0034-4885/71/7/076401..

　　 [3] ^AK Yetisen; H Butt; F da Cruz Vasconcellos; Y Montelongo; CAB Davidson; J Blyth; JB Carmody; S Vignolini; U Steiner; JJ Baumberg; TD Wilkinson; CR Lowe (2013). "Light-Directed Writing of Chemically Tunable Narrow-Band Holographic Sensors". Advanced Optical Materials. 2 (3): 250–254. doi:10.1002/adom.201300375..

　　 [4] ^Letter from James Gregory to John Collins, dated 13 May 1673. Reprinted in: Rigaud, Stephen Jordan, ed. (1841). Correspondence of Scientific Men of the Seventeenth Century…. 2. Oxford University Press. pp. 251–5. especially p. 254.

　　 [5] ^Hopkinson, F.; Rittenhouse, David (1786). "An optical problem, proposed by Mr. Hopkinson, and solved by Mr. Rittenhouse". Transactions of the American Philosophical Society. 2: 201–6. doi:10.2307/1005186. JSTOR 1005186..

　　 [6] ^Thomas D. Cope (1932) "The Rittenhouse diffraction grating". Reprinted in: Rittenhouse, David (1980). Hindle, Brooke, ed. The Scientific Writings of David Rittenhouse. Arno Press. pp. 377–382. ISBN 9780405125683. (A reproduction of Rittenhouse's letter re his diffraction grating appears on pp. 369–374.).

　　 [7] ^Frauhofer, Jos (1821). "Neue Modifikation des Lichtes durch gegenseitige Einwirkung und Beugung der Strahlen, und Gesetze derselben" [New modification of light by the mutual influence and the diffraction of [light] rays, and the laws thereof]. Denkschriften der Königlichen Akademie der Wissenschaften zu München (Memoirs of the Royal Academy of Science in Munich). 8: 3–76..

　　 [8] ^Fraunhofer, Jos (1823). "Kurzer Bericht von den Resultaten neuerer Versuche über die Gesetze des Lichtes, und die Theorie derselben" [Short account of the results of new experiments on the laws of light, and the theory thereof]. Annalen der Physik. 74 (8): 337–378. Bibcode:1823AnP....74..337F. doi:10.1002/andp.18230740802..

　　 [9] ^Turner, G. L'E. (1967). "The contributions to Science of Friedrich Adolph Nobert". Bulletin of the Institute of Physics and the Physical Society. 18 (10): 338–348. doi:10.1088/0031-9112/18/10/006..

　　 [10] ^Warner, Deborah J. (1971). "Lewis M. Rutherfurd: Pioneer Astronomical Photographer and Spectroscopist". Technology and Culture. 12 (2): 190–216. doi:10.2307/3102525. JSTOR 3102525..

　　 [11] ^Warner, Deborah J. (1988). The Michelson Era in American Science 1870-1930. New York: American Institute of Physics. pp. 2–12..

　　 [12] ^Hentschel, Klaus (1993). "The Discovery of the Redshift of Solar Fraunhofer Lines by Rowland and Jewell in Baltimore around 1890" (PDF). Historical Studies in the Physical and Biological Sciences. 23 (2): 219–277. doi:10.2307/27757699. JSTOR 27757699..

　　 [13] ^Sweeetnam, George (2000). The Command of Light: Rowland's School of Physics and the Spectrum. Philadelphia: American Philosophical Society. ISBN 978-08716-923-82..

　　 [14] ^Feynman, Richard (1985). QED: The Strange Theory of Light and Matter. Princeton University Press. ISBN 978-0691083889.. [15] ^Ambient Diagnostics by Yang Cai -- CRC Press 2014 Page 267.

　　 [16] ^https://web.archive.org/web/20221028214305/http://www.nnin.org/sites/default/files/files/Karen_Rama_USING_CDs_AND_DVDs_AS_DIFFRACTION_GRATINGS_0.pdf.

　　 [17] ^Xu, Zhida; Han, Kevin; Khan, Ibrahim; Wang, Xinhao; Liu, Logan (2014). "Liquid refractive index sensing independent of opacity using an optofluidic diffraction sensor". Optics Letters. 39 (20): 6082–6085. arXiv:1410.0903. Bibcode:2014OptL...39.6082X. doi:10.1364/OL.39.006082. PMID 25361161..

　　 [18] ^"Step 17". Nook Simple Touch with GlowLight Teardown. iFixit. 2012..

　　 [19] ^Barreiro, Jesús J.; Pons, Amparo; Barreiro, Juan C.; Castro-Palacio, Juan C.; Monsoriu, Juan A. (March 2014). "Diffraction by electronic components of everyday use" (PDF). American Journal of Physics. 82 (3): 257–261. Bibcode:2014AmJPh..82..257B. doi:10.1119/1.4830043. hdl:10251/54288..

　　 [20] ^Baskin, R.J.; Roos, K.P.; Yeh, Y. (October 1979). "Light diffraction study of single skeletal muscle fibers". Biophys. J. 28 (1): 45–64. Bibcode:1979BpJ....28...45B. doi:10.1016/S0006-3495(79)85158-9. PMC 1328609. PMID 318066..

　　 [21] ^Stavenga, D. G. (2014). "Thin Film and Multilayer Optics Cause Structural Colors of Many Insects and Birds" (PDF). Materials Today: Proceedings. 1: 109–121. doi:10.1016/j.matpr.2014.09.007..

　　 [22] ^Roberts, N. W.; Marshall, N. J.; Cronin, T. W. (2012). "High levels of reflectivity and pointillist structural color in fish, cephalopods, and beetles" (PDF). Proceedings of the National Academy of Sciences. 109 (50): E3387. Bibcode:2012PNAS..109E3387R. doi:10.1073/pnas.1216282109. PMC 3528518. PMID 23132935..

　　 [23] ^Stavenga, D. G.; Leertouwer, H. L.; Wilts, B. D. (2014). "Coloration principles of nymphaline butterflies - thin films, melanin, ommochromes and wing scale stacking". Journal of Experimental Biology. 217 (12): 2171–2180. doi:10.1242/jeb.098673. PMID 24675561..

　　 [24] ^Van Der Kooi, C. J.; Wilts, B. D.; Leertouwer, H. L.; Staal, M.; Elzenga, J. T. M.; Stavenga, D. G. (2014). "Iridescent flowers? Contribution of surface structures to optical signaling" (PDF). New Phytologist. 203 (2): 667–73. doi:10.1111/nph.12808. PMID 24713039..

　　 [25] ^Lee, David W. (2007). Nature's Palette: The Science of Plant Color. University of Chicago Press. pp. 255–6. ISBN 978-0-226-47105-1..

　　 [26] ^Van Der Kooi, C. J.; Dyer, A. G.; Stavenga, D. G. (2015). "Is floral iridescence a biologically relevant cue in plant-pollinator signaling?" (PDF). New Phytologist. 205 (1): 18–20. doi:10.1111/nph.13066. PMID 25243861..

　　 [27] ^Hsiung, Bor-Kai; Siddique, Radwanul Hasan; Stavenga, Doekele G.; Otto, Jürgen C.; Allen, Michael C.; Liu, Ying; Lu, Yong-Feng; Deheyn, Dimitri D.; Shawkey, Matthew D. (2017-12-22). "Rainbow peacock spiders inspire miniature super-iridescent optics". Nature Communications (in 英语). 8 (1): 2278. Bibcode:2017NatCo...8.2278H. doi:10.1038/s41467-017-02451-x. ISSN 2041-1723. PMC 5741626. PMID 29273708..

　　 [28] ^Lee 2007，第 41 页.

　　 [29] ^"Colouring in the fossil past". News. Natural History Museum. 15 March 2006..

　　 [30] ^Können, G. P. (1985). Polarized Light in Nature. Cambridge University Press. pp. 72–73. ISBN 978-0-521-25862-3..