运动学

                     

贡献者： addis

　　 （本文根据 CC-BY-SA 协议转载自原搜狗科学百科对英文维基百科的翻译）

　　 运动学是经典力学的一个分支，描述了点、体(对象)和体系统(对象组)的运动，而不考虑引起运动的力。[1][2][3]运动学作为一个研究领域，通常被称为 “运动的几何”，偶尔也被视为数学的一个分支。[4][5][6]运动学问题首先描述系统的几何形状，并声明系统内任何已知点的位置、速度和/或加速度值的初始条件。然后，使用几何参数，可以确定系统任何未知部分的位置、速度和加速度。对力如何作用于物体的研究属于动力学范畴，而不是运动学。有关更多详细信息，请参见分析动力学。

　　 运动学在天体物理学中用于描述天体的运动和这些天体的集合。在机械工程、机器人学和生物力学中[7]运动学用于描述由连接部件(多连杆系统)组成的系统的运动，例如发动机、机械臂或人体骨骼。

　　 几何变换，也称为刚性变换，用于描述机械系统中部件的运动，简化了运动方程的推导。它们也是动态分析的核心。

　　 运动学分析是测量用于描述运动的运动学量的过程。例如，在工程中，运动学分析可用于找到给定机构的运动范围，并反向工作，使用运动学综合来设计所需运动范围的机构。[8] 此外，运动学将代数几何学应用于研究机械系统或机构的机械效益。

1. 词源

　　 术语运动学是英文的 A.M. Ampère cinématique[9]，来源于希腊语词根的 κίνημα 电影院(“运动，运动”)，而词根来源于κινεῖν kinein(“移动”)。[10][11]

　　 运动学和 cinématique 与法语单词 cinéma 有关，但两者都不是直接从它派生出来的。然而，它们确实有一个共同的词根，因为 cinéma 来自 CINématography 的简称 “电影放映机和照相机”，再次来自运动的希腊语单词，但也来自写作的希腊语单词。[12]

2. 非旋转参照系中粒子轨迹的运动学

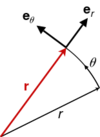
　　 平面极坐标中的运动矢量。请注意，不限于二维空间，而是任何更高维度的平面。

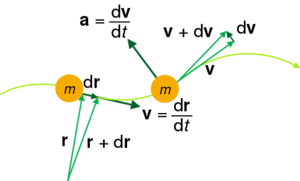
　　 粒子运动学是对粒子轨迹的研究。粒子的位置被定义为从坐标框架的原点到粒子的坐标向量。例如，假设一个距离您家向南 50 米的塔，坐标系位于您家，这样东方是 x 方向，北方是 y 方向，那么塔底部的坐标向量是 $r=(0,50,0)$。如果塔是 50 m 高，则到达塔顶的坐标向量为 $r=(0,50,0)$。

　　 在大多数情况下，三维坐标系用于定义粒子的位置。然而，如果粒子被约束在表面上移动，二维坐标系就足够了。如果没有参考系来描述这些观测，物理学中的所有观测都是不完整的。

　　 粒子的位置向量是从参考系的原点到粒子的向量。它既表示点到原点的距离，也表示点到原点的方向。在三维空间中，点的位置 P 可以表示为

　　 这里 $x_P, y_P,$ 和 $z_P$ 是笛卡尔坐标，$\hat{i}, \hat{j}$ 和 $\hat{k}$ 是沿着 $x, y, z$ 坐标轴的单位向量。位置向量的大小 $\left| \mathbf{P} \right|$ 给出点和原点之间的距离 $\mathbf{P}$

位置向量的方向余弦提供了方向的定量测量。需要注意的是，粒子的位置向量不是唯一的。给定粒子的位置向量相对于不同的参考系是不相同的。

　　 粒子的轨迹是时间的矢量函数，$\mathbf{P}(t)$，它定义了运动粒子所描述的曲线，由

这里，坐标 $x_P, y_P,$ 和 $z_P$ 都是时间的函数。

2.1 速度和速度

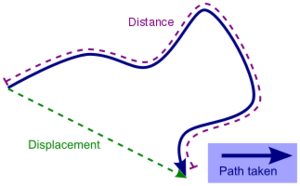
　　 粒子的速度是描述运动方向和粒子运动大小的矢量。从数学上讲，一个点的位置向量相对于时间的变化率是该点的速度。考虑粒子的两个位置之差除以时间间隔形成的比率。该比率称为该时间间隔内的平均速度，定义为速度=位移/时间 $$\overline{V} = \frac{\Delta \mathbf{P}}{\Delta t}~,$$ 其中 $\Delta \mathbf{P}$ 是位置向量在时间间隔 $\Delta t$ 上的变化。

　　 当时间间隔 $\Delta t$ 越来越小时，平均速度成为位置矢量的时间导数， $$\mathbf {V} = \lim_{\Delta t \to 0} \frac{\Delta \mathbf{P}}{\Delta t} = \frac{d \mathbf{P}}{dt} = \dot{\mathbf{P}} = \dot{x}\hat{\imath} + \dot{y}\hat{\jmath} + \dot{z}\hat{k}~$$。 因此，速度是点位置变化的时间速率，点表示这些函数 $\dot{x}$、$\dot{y}$ 和 $\dot{z}$ 相对于时间的导数。此外，在粒子沿其路径占据的每个位置，速度都与粒子的轨迹相切。请注意，在非旋转坐标系中，坐标方向的导数不被认为是常数，因为它们的方向和幅度是常数。

　　 物体的速度是其速度的大小。它是一个标量： $$\left| \mathbf{V} \right| = \left| \dot{\mathbf{P}} \right| = \frac{ds}{dt}~,$$ 其中 s 是沿着粒子轨迹测量的弧长。粒子随时间移动的弧长 ds 是非递减量。因此，$\frac{ds}{dt}$ 是非负的，这意味着速度也是非负的。

2.2 加速度

　　 速度矢量可以在大小和方向上变化，或者同时在两个方向上变化。因此，加速度既考虑了速度矢量大小的变化率，也考虑了该矢量方向的变化率。类似于用位移定义速度，也可以用速度定义加速度矢量。它由速度矢量的变化率定义。 $$\overline{A} = \frac{\Delta \mathbf{V}}{\Delta t}~,$$ 其中 $\Delta \mathbf{v}$ 是速度矢量 $\Delta t$ 是时间间隔。

　　 当时间间隔接近零时，粒子的加速度是平均加速度的极限， $$\mathbf {A} = \lim_{\Delta t \to 0} \frac{\Delta \mathbf{V}}{\Delta t} = \frac{d \mathbf{V}}{dt} = \dot{\mathbf{V}} = \dot{v}_x\hat{\imath} + \dot{v}_y\hat{\jmath} + \dot{v}_z\hat{k}~$$方程 1) 或者 $$\mathbf{A}=\ddot{P}=\ddot{x}_p\hat{\imath}+\ddot{y}_p\hat{\imath}+\ddot{z}_p\hat{k}~$$ 因此，加速度是该粒子速度矢量的一阶导数和位置矢量的二阶导数。请注意，在非旋转坐标系中，坐标方向的导数不被认为是常数，因为它们的方向和幅度是常数。

　　 物体的加速度的幅值是其矢量|A|的大小。它是一个标量: $$\left| \mathbf{A} \right| = \left| \dot{\mathbf{V}} \right| = \frac{dV}{dt}~,$$

2.3 相对位置向量

　　 相对位置向量是定义一个点相对于另一个点的位置的向量。这是两点的位置差异。一点的位置 $A$ 相对于另一点 $B$ 只是他们位置的不同 $$\mathbf{P}_{A/B}$=$\mathbf{P}_{A}$-$\mathbf{P}_{B}~,$$ 这是它们的位置向量的分量之间的差异。

　　 如果点 A 具有位置坐标 $\mathbf{P}_{A}=(X_{A},Y_{A},Z_{A})$

　　 如果点 B 具有位置坐标 $\mathbf{P}_{B}=(X_{B},Y_{B},Z_{B})$

　　 那么点的位置 A 相对于点 B 它们的坐标之间的差是: $$\mathbf{P}_{A/B}$=$\mathbf{P}_{A}-\mathbf{P}_{B}$=$(X_{A}-X_{B},Y_{A}-Y_{B},Z_{A}-Z_{B})~$$

2.4 相对速度

　　 一个点相对于另一个点的速度仅仅是它们的速度之差 $$\mathbf{V}_{A/B}$=$\mathbf{V}_{A}-\mathbf{V}_{B}~$$ 这是它们速度分量之间的差异。

　　 如果点 A 有速度分量 $\mathbf{V}_{A}=(V_{A_x},V_{A_y},V_{A_z})$

　　 指向 B 有速度分量 $\mathbf{V}_{B}=(V_{B_x},V_{B_y},V_{B_z})$

　　 那么点 A 的速度相对于点 B 它们的速度差是: $$\mathbf{V}_{A/B} = \mathbf{V}_A - \mathbf{V}_B = \left( V_{Ax} - V_{Bx}, V_{Ay} - V_{By}, V_{Az} - V_{Bz} \right)~$$ 或者，可以通过计算相对位置矢量的时间导数来获得相同的结果 $\mathbf{r}_{B/A}$。

　　 在速度接近光速的情况下 c(通常在 95% 以内)另一种相对速度的方案称为快度，它取决于 V 与 c 的比率，用于狭义相对论。

2.5 相对加速度

　　 一点的加速度 C 相对于另一点 B 的加速度，仅仅是它们的加速度之差。 $$\mathbf{A}_{C/B}$=$\mathbf{A}_{C}-\mathbf{A}_{B}~$$ 这是它们的加速度分量之间的差值。

　　 如果点 C 有加速度分量 $\mathbf{A}_{C}=(A_{C_x},A_{C_y},A_{C_z})$

　　 指向 B 有加速度分量 $\mathbf{A}_{B}=(A_{B_x},A_{B_y},A_{B_z})$

　　 那么点 C 相对于点 B 的加速度差是: $$\mathbf{A}_{C/B} = \mathbf{A}_{C}-\mathbf{A}_{B} = (A_{C_x}-A_{B_x},A_{C_y}-A_{B_y},A_{C_z}-A_{B_z})~,$$ 或者，可以通过计算相对位置矢量的二阶时间导数来获得相同的结果 $\mathbf{P}_{B/A}$。

3. 恒定加速度下的粒子轨迹

　　 对于恒定加速度的情况，微分方程式 1)可以积分为加速度矢量 ${A}$ 在大小和方向上是不变的。这被称为匀加速运动。在这种情况下，速度 $V(t)$ 和轨迹 $P(t)$ 可以通过积分加速度方程 $A$ 得到[13]。

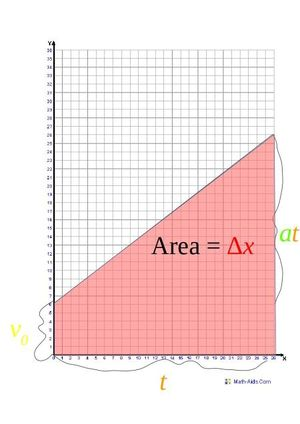
　　 假设位置的初始条件已知，$t=0$ 时，$p=\mathbf{P}_0$, $v=\mathbf{V}_0$，第一次积分可以得到粒子速度与时间的函数关系。 $$\mathbf{V}(t)=\mathbf{V}_{0} + \int_{0}^{1}\mathbf{Ad}\tau = \mathbf{V}_{0}+\mathbf{A}_{t}~.$$ 第二次积分产生它的路径(轨迹)， $$\mathbf{P}(t)=\mathbf{P}_{0}+\int_{0}^{1}\mathbf{V}(\tau )d\tau=\mathbf{P}_{0}+\int_{0}^{1}(\mathbf{V}_{0}+\mathbf{A}\tau)d\tau=\mathbf{P}_{0}+\mathbf{V}_{0}t+\frac{1}{2}\mathbf{A}t^2~.$$ 可以推导出位移、速度、加速度和时间之间的关系。因为加速度是恒定的， $$\mathbf{A} = \frac{\Delta \mathbf{V}}{\Delta t}=\frac{\mathbf{V}-\mathbf{V_0}}{t}~,$$ 代入上述方程得到: $$\mathbf{P}(t)=\mathbf{P}_{0}+\Big(\frac{\mathbf{V}+\mathbf{V_0}}{2}\Big )t~$$ 速度、位置和加速度之间的关系没有明确的时间相关性，可以通过求解时间的平均加速度，并进行替换和简化 $$t=\frac{\mathbf{V}-\mathbf{V_0}}{A}~$$

其中 $\circ$ 表示点积，这是合适的，因为积是标量而不是向量。 点积可以用角度的余弦值 $\alpha$ 在向量和矢量的大小之间替代，在这种情况下：

　　 在加速度总是在运动方向的情况下，矢量之间的角度（$\alpha$）是 0，所以 $\cos 0 = 1$，故

这可以使用向量大小的符号来简化 $\\|A\\| = a, \\|V\\| = v, \\|P - P_0\\| = \Delta x$，这里 $\Delta x$ 可以是任何曲线路径，因为沿着该路径应应用恒定的切向加速度，所以 这将粒子运动的参数方程简化为速度与位置的笛卡尔关系。当时间未知时，这种关系很有用。我们也知道 $$\Delta x = \int(v)dt~$$ 或者 $\Delta$x, 是 v-t , 图形下的面积。 我们可以通过增加顶部区域和底部区域来获取 $\Delta$x。底部区域是一个矩形，矩形的面积是 $A \cdot B$。其中 $A$ 是宽，$B$ 是高。既然这样 $A=t$ 和 $B=v_0$（请注意 $A$ 这里不同于加速度 $a$ 中）。这意味着底部区域是 $tv_0$。现在让我们找到顶部区域（三角形）。三角形的面积是 $\frac{1}{2}BH$ 其中 $B$ 是底，$H$ 是高。在这种情况下，$B=t$ & $H=at$ 或者 $A = \frac{1}{2}BH = \frac{1}{2}att = \frac{1}{2}at^2 = \frac{at^2}{2}$。在等式中增加 $tv_0$ 和 $\frac{at^2}{2}$,$\Delta x = tv_0 + \frac{at^2}{2}$。当最终速度 $v$ 未知时，这个公式很有用。

4. 圆柱-极坐标中的粒子轨迹

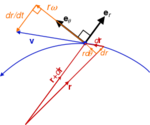
　　 用 $x-y$ 平面上的极坐标来表示粒子 $p(t) = (x(t), y(t), z(t))$ 的轨迹通常是很方便的。在这种情况下，它的速度和加速度采用一种方便的形式。

　　 回想一下，粒子 $p$ 的轨迹是由其在固定参考坐标系中的测量的坐标向量 $\mathbf{p}(t)$ 跟踪其轨迹，这是空间中的曲线，曲线如下给出: $$\mathbf{P}(t) = X(t)\hat{i} + Y(t)\hat{j} + Z(t)\hat{k}~,$$ 其中 $\hat{i}$，$\hat{j}$ 和 $\hat{k}$ 是沿着 $X, Y \text{和} Z$ 轴的单位向量。 考虑仅在圆柱 R（t）＝C 的表面上移动的粒子 P，可以将固定框架 F 的 Z 轴与圆柱体轴线对齐。然后，X 轴平面内的这个轴的角度 $\theta$ 可以用来定义其轨迹， $$\mathbf{P}(t) = \mathbf{R}\cos \theta(t) \hat{i} + \mathbf{R} \sin \theta(t) \hat{j} + Z(t) \hat{k}~.$$ 通过引入径向和切向单位矢量，可以简化 P(t)的柱坐标: $$\mathbf{e}_r = \cos \theta(t) \hat{i} + \sin \theta(t) \hat{j}~,$$ $$\mathbf{e}_{\theta} = -\sin \theta(t) \hat{i} + \cos \theta(t) \hat{j}~,$$ 和它们的初等微积分时间导数:

使用这些符号，$\mathbf{P}(t)$ 变成以下形式： 其中在粒子仅在半径为 $r$ 的圆柱体表面上移动的情况下为常数。

　　 一般情况下，轨迹 $\mathrm{P}(t)$ 不被约束在圆柱上，因此半径 $r$ 随时间变化，圆柱极坐标中的粒子轨迹变为：

其中 R, $\theta$ 和 Z 可能是时间的连续可微函数，为了简便起见，函数符号被去掉了。速度矢量 $\mathbf{V}_P $ 是轨迹 $ \mathbf{P}$(t) 的时间导数，即： $$\mathbf{V}_P = \frac{d}{dt} (\mathbf{R}e_r + Z\hat{k}) = \dot{\mathbf{R}}e_r + \mathbf{R}\dot{e_r} + \dot{Z}\hat{k} = \dot{\mathbf{R}}e_r + R\dot{\theta}e_{\theta} + \dot{Z}\hat{k}~$$ 同样，加速度 $\mathbf{A}_P $ 是速度 $\mathbf{V}_P $ 的时间导数，由下式给出： $$\mathbf{A}_P = \frac{d}{dt} (\dot{\mathbf{R}}e_r + R\dot{\theta}e_{\theta} + \dot{Z}\hat{k}) = (\ddot{\mathbf{R}} - R\dot{\theta}^2)e_r + (R\ddot{\theta} + 2\dot{\mathbf{R}}\dot{\theta})e_{\theta} + \ddot{Z}\hat{k}~$$ 术语 $-R\dot{\theta}^2e_r$ 作用于路径上该点的曲率中心，通常称为向心加速度。术语 $2\dot{R}\dot{\theta}e_{\theta}$ 被称为科里里奥利加速度。

4.1 恒定半径

　　 如果粒子的轨迹被约束在圆柱体上，那幺半径 r 是常数，速度和加速度向量也会简化。vp 的速度是轨迹 p（t）的时间导数。

加速度矢量变为:

4.2 平面圆形轨迹

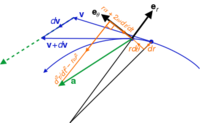
　　 当在 Z 轴上没有运动时，在圆柱上出现粒子轨迹的特殊情况： $$\mathbf{P}(t) = R \mathbf{e}_r + Z_0 \mathbf{\hat{k}}~,$$ 其中 $R$ 和 $Z_0$ 是常数。在这种情况下，速度 $\mathbf{V}_P$ 由下式给出:

　　 $$\mathbf{V}_P = \frac{d}{dt}(R \mathbf{e}_r + Z_0 \mathbf{\hat{k}}) = R \dot{\theta} \mathbf{e}_{\theta} = R \omega \mathbf{e}_{\theta}~,$$

　　 其中

　　 $\omega = \dot{\theta},$

　　 是单位矢量 $\mathbf{e}_{\theta}$ 在绕圆柱体 $Z$ 轴的角速度。

　　 加速度 $\mathbf{A}_P$ 粒子的 P 现在由下式给出: $$\mathbf{A}_P = \frac{d}{dt}(R \dot{\theta} \mathbf{e}_{\theta}) = -R \dot{\theta}^2 \mathbf{e}_r + R \ddot{\theta} \mathbf{e}_{\theta}~.$$ 设 $$a_r = -R \dot{\theta}^2, \quad a_{\theta} = R \ddot{\theta}~,$$ 分别称为射线和切线分量加速度。

　　 角速度和角加速度的符号通常定义为 $$\omega = \dot{\theta}, \quad \alpha = \ddot{\theta}~,$$ 所以圆轨迹的径向和切向加速度分量也写作 $$a_r = -R \omega^2, \quad a_{\theta} = R \alpha~.$$

5. 物体在平面内运动的点轨迹

　　 通过在每个零件上附加一个参考坐标系并确定各个参考坐标系是如何相对移动的，来分析机械系统部件的运动。如果零件的结构刚度足够大，则可以忽略其变形，并使用刚性变换来定义这种相对运动。这就把对复杂机械系统各部分运动的描述，简化为描述各部分的几何结构和各部分相对于其它部分的几何关联的问题。

　　 几何学是研究在空间以各种方式变换时保持不变的图形的性质——更严格地说，是研究在一组变换下的不变量[18]。这些变换可以导致三角形在平面上的位移，同时留下顶点的角度和顶点之间的距离不变。运动学通常被描述为应用几何学，其中机械系统的运动是用欧几里德几何学的刚性变换来描述的。

　　 平面中点的坐标是 $r^2$(二维空间)中的二维向量。刚性变换是那些保持任意两点之间距离的变换。n-维空间中的刚性变换集称为特殊的欧几里德群 $r^n$，并表示为 SE(n)。

5.1 位移和运动

　　 机械系统的一个部件相对于另一个部件的位置是通过引入参考坐标系来定义的，比如说 m，它相对于另一个固定的框架 f 移动。m 相对于 f 的刚体变换或位移定义了两个分量的相对位置。位移由旋转和平移的组合组成。。

　　 m 相对于 f 的所有位移的集合称为 m 的配置空间。在该配置空间中，从一个位置到另一个位置的光滑曲线是一个连续的位移集合，称为 m 相对于 f 的运动。

5.2 矩阵表示

　　 平面 R2 中旋转和平移的组合可以用一种称为齐次变换的 $3 \times 3 $ 矩阵表示。$ 3 \times 3 $ 齐次变换由 $ 2 \times 2 $ 旋转矩阵 $ A(\phi) $) 和 $2 \times 1 $ 平移向量构成 $\mathbf{d} = (d_x, d_y)$，如： $$\mathbf{T}(\phi, \mathbf{d}) = \begin{bmatrix}A(\phi) & \mathbf{d} \\0 & 1 \end{bmatrix} = \begin{bmatrix}\cos \phi & -\sin \phi & d_x \\\sin \phi & \cos \phi & d_y \\0 & 0 & 1\end{bmatrix}~.$$ 这些齐次变换对平面 $ z=1 $ 中的点执行刚性变换，即对坐标 $\mathbf{p} = (x, y, 1) $ 的点行刚性变换。

　　 特别是，令 $\mathbf{p}$ 定义与固定框架重合的参考框架 $\mathbf{m}$) 中的点的坐标。那么，当 $\mathbf{m}$ 的原点被相对于 $\mathbf{p}$ 的原点的平移向量 $\mathbf{d} $ 置换，并被相对于 $ y $ 轴的角度 $\phi$ 旋转时，$\mathbf{m}$ 中的新的坐标由以下公式给出： $$\mathbf{P} = \mathbf{T}(\phi, \mathbf{d}) \mathbf{p} = \begin{bmatrix}\cos \phi & -\sin \phi & d_x \\\sin \phi & \cos \phi & d_y \\0 & 0 & 1\end{bmatrix}\begin{Bmatrix}x \\ y \\1\end{Bmatrix}~.$$ 齐次变换代表仿射变换。这个公式是必要的，因为平移不是线性变换 $ r^2 $。然而，使用射影几何 $r^2 $，使得 $ r^2 $ 是 $ r^3 $ 的子集，平移变成仿射线性变换。

6. 纯平移

　　 如果刚体移动，使其参考坐标系 $m$ 不相对于固定坐标系旋转（$\phi = 0$），则该运动称为纯平移。在这种情况下，物体中每个点的轨迹是 $m$ 原点轨迹 $\mathbf{d}(t)$ 的偏移，即：

　　 $\mathbf{P}(t) = [\mathbf{T}(0, \mathbf{d}(t))]\mathbf{p} = \mathbf{d}(t) + \mathbf{p}$.

　　 因此，对于纯平移的物体，每一点的速度和加速度由下式给出：

　　 $\mathbf{V}_{\mathbf{P}} = \dot{\mathbf{P}}(t) = \dot{\mathbf{d}}(t) = \mathbf{V}_O, \quad \mathbf{A}_{\mathbf{P}} = \ddot{\mathbf{P}}(t) = \ddot{\mathbf{d}}(t) = \mathbf{A}_O,$

　　 其中，点表示相对于时间的导数，$\mathbf{v}_O$ 和 $\mathbf{a}_O$ 分别表示移动轨迹 $m$ 原点的速度和加速度。回忆一下，$m$ 中的坐标向量 $\mathbf{p}$ 是常数，因此其导数为零。

7. 物体围绕固定轴的旋转

　　 旋转或角度运动学是对对象旋转的描述。[20]对旋转的描述需要一些描述方向的方法。常用的描述包括欧拉角和由代数积引起的转动的运动学。

　　 在下文中，注意力仅限于围绕固定方向的轴的简单旋转。为方便起见，选择 Z 轴。

　　 位置

　　 这允许将旋转描述为平面参考框架 M 相对于固定于该共享 Z 轴上的 F 的角位置。M 中的坐标 $P=(x,y)$ 与 $f$ 中的坐标 $P=(x,y)$ 通过矩阵方程相关： $$\mathbf{P}(t) =[A(t)]\mathbf{p}~,$$

　　 其中 $$[A(t)] = \begin{bmatrix}\cos \theta(t) & -\sin \theta(t) \\\sin \theta(t) & \cos \theta(t)\end{bmatrix}~,$$ 是旋转矩阵，它定义 M 相对于时间的角度位置作为时间的函数。

　　 速度

　　 如果点 p 在 M 中不移动，其在 F 中的速度由下式给出 $$\mathbf{V_P} = \dot{\mathbf{P}} = [\dot{A}(t)]\mathbf{p}~.$$ 消除坐标 $p$ 并将其写为对轨迹 $p(t)$ 的运算是很方便的， $$\mathbf{V_P} = [\dot{A}(t)][A(t)]^{-1}\mathbf{P} = [\Omega]\mathbf{P}~,$$ 其中矩阵

　　 $$\Omega] = \begin{bmatrix}0 & -\omega \\\omega & 0\end{bmatrix}~,$$即 M 相对于 F 的角速度矩阵。参数 $\omega$ 是角 $\theta$ 的时间导数， $$\omega = \frac{d\theta}{dt}~.$$

　　 加速度

　　 F 中 $\mathbf{P}(t)$ 的加速度通过速度的时间导数获得，

变成了 其中 为 $M$ 在 $F$ 上的角加速度矩阵, 并且 旋转的描述涉及这三个量:

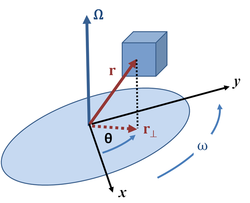
• 角位置：从旋转轴上选定的原点到目标点的定向距离是定位点的向量 r（t）。向量 R（t）在垂直于旋转轴的平面上具有一定的投影 r（t）。然后，该点的角度位置是从参考轴（通常是正 X 轴）到已知旋转意义的向量 R（t）的角度τ（通常由右手规则给出）。
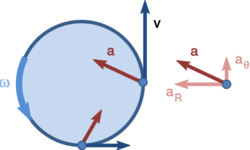
• 角速度 :角速度 $\omega$ 是角位置的速率θ相对于时间 t 的变化: $$\omega = \frac{d\theta}{dt}~.$$ 角速度在图 1 中用矢量 $\Omega$ 表示，该矢量 $\Omega$ 指向旋转轴，其大小 $\omega$ 和意义由旋转方向决定，如右手法则所示。
• 角加速度：角加速度 $\alpha$ 的大小是角速度 $\omega$ 相对于时间 t 变化的速率： $$\alpha = \frac{d\omega}{dt}~.$$ 平移运动学方程可以很容易地推广到平面转动运动学中，用简单的变量交换求解恒定角加速度： $$\omega_f = \omega_i + \alpha t~$$ $$\theta_f - \theta_i = \omega_i t + \frac{1}{2} \alpha t^2~$$ $$\theta_f - \theta_i = \frac{1}{2} (\omega_f + \omega_i) t~$$ $$\omega_f^2 = \omega_i^2 + 2 \alpha (\theta_f - \theta_i)~$$ 这里 $\theta_i$ 和 $\theta_f$ 分别是初始和最终角度位置，$\omega_i$) 和 $\omega_f$ 分别是初始速度和最终角速度，$\alpha$ 是恒定的角加速度。虽然空间中的位置和空间中的速度都是真实的矢量（根据它们在旋转下的特性），但角速度也是真实的矢量，角度本身不是真实的矢量。

8. 物体三维运动的点轨迹

　　 运动学中的重要公式定义了运动物体在三维空间中跟踪轨迹时的速度和加速度。这对于一个物体的质心特别重要，它用牛顿第二定律或拉格朗日方程导出运动方程。

8.1 位置

　　 为了定义这些公式，机械系统的部件 B 的运动是由一组旋转[A（t）]和平移 D（t）定义的，其组合成齐次变换[t（t）]＝[a（t），d（t）]。如果 p 是在移动参考坐标系 m 中测量的点 p 在 b 中的坐标，则在 f 中跟踪的该点的轨迹由下式给出：

这种符号不能区分 $\mathbf{P} = (X, Y, Z, 1)$ 和 $\mathbf{P} = (X, Y, Z)$，这在上下文中希望是很清楚的。

　　 这个 $\mathbf{p}$ 的轨迹方程可以倒过来计算 $m$ 中的坐标向量 $\mathbf{p}$，如下所示：

这个表达式使用了旋转矩阵的转置也是其逆变换的事实，即：

8.2 速度

　　 点 P 沿其轨迹 P（t）的速度作为该位置矢量的时间导数获得， $$\mathbf{V}_P = \left[ \dot{\mathbf{T}}(t) \right] \mathbf{p} = \begin{Bmatrix} \mathbf{V}_P \\ 0 \end{Bmatrix} = \begin{bmatrix} \mathbf{A}(t) & \dot{\mathbf{d}}(t) \\ 0 & 1 \end{bmatrix} \begin{Bmatrix} \mathbf{p} \\1 \end{Bmatrix} = \begin{bmatrix} \dot{\mathbf{A}}(t) & \dot{\mathbf{d}}(t) \\ 0 & 0 \end{bmatrix} \begin{Bmatrix} \mathbf{p} \\ 1 \end{Bmatrix}~.$$ 点表示相对于时间的导数；因为 $\mathbf{p}$ 是常数，它的导数为零。

　　 这个公式可以通过对在固定框架中测得的 p(t) 的轨迹进行运算来获得 p 的速度。将 p 的逆变换代入速度方程得到：

矩阵 $[\mathbf{S}]$ 由下式给出: 其中 $$[\Omega] = \dot{\mathbf{A}} \mathbf{A}^{\top}~,$$ 是角速度矩阵。

　　 乘以算子 $[\mathbf{S}]$，速度 $\mathbf{V}_P$ 的公式为:

　　 $\mathbf{V}_P = [\Omega](\mathbf{P} - \mathbf{d}) + \dot{\mathbf{d}} = {\omega} \times \mathbf{R}_{P/O} +\mathbf{V}_O,$

　　 其中，矢量 ${\omega}$ 是从矩阵 $[\Omega]$ 的分量中获得的角速度矢量；矢量

　　 $\mathbf{R}_{P/O} = \mathbf{P} - \mathbf{d},$

　　 是 P 相对于移动框架 m 的原点 O 的位置；以及

　　 $\mathbf{V}_O = \dot{\mathbf{d}},$

　　 是原点的速度 $O$。

8.3 加速度

　　 在运动体 B 中的点 p 的加速度是作为其速度矢量的时间导数获得的： $$A_P = \frac{d}{dt} V_P = \frac{d}{dt} \left( [S]P \right) = \dot{[S]} P + [S] \dot{P} = \dot{[S]} P + [S] [S] P~.$$ 这个方程可以首先通过计算来扩展 $$\dot{[S]} = \begin{bmatrix} \dot{\Omega} & -\dot\Omega {d} -\Omega \dot{d}+ \ddot{d} \\ 0 & 0 \end{bmatrix} = \begin{bmatrix} \dot{\Omega} & -\dot\Omega {d} - \Omega V_O + A_O \\ 0 & 0 \end{bmatrix}~$$ 和 $$[S]^2 = \begin{bmatrix} \Omega & -\Omega d + V_O \\ 0 & 0 \end{bmatrix}^2 = \begin{bmatrix} \Omega^2 & -\Omega^2 d + \Omega V_O \\ 0 & 0 \end{bmatrix}~.$$ 加速度 $A_P$ 现在可以变成: $$\mathbf{A}_P = \dot{\Omega} (\mathbf{P - d}) + A_O + \Omega^2 (\mathbf{P - d})~,$$ 或者 $$\mathbf{A}_P = \alpha \times \mathbf{R}_{P/O} + \omega \times \omega \times \mathbf{R}_{P/O} + \mathbf{A}_O~,$$ 其中 $\alpha$ 是从角速度矩阵的导数获得的角加速度矢量; $$\mathbf{R}_{P/O}=\mathbf{P}-\mathbf{d}~$$ 是相对位置向量(P 相对于移动框架 M 的原点 O)； $$\mathbf{A}_{O}=\ddot{d}~$$ 是移动框架原点的加速度 M。

9. 运动约束

　　 运动约束是对机械系统部件运动的约束。运动约束可以被认为有两种基本形式：（i）由定义系统结构的铰链、滑块和凸轮关节产生的约束，称为完整约束；（ii）对系统速度施加的约束，如平面上溜冰鞋的刀口约束，或滚动而不滑动的圆盘或球体与平面接触，这被称为非完整约束。下面是一些常见的例子。

9.1 运动耦合

　　 运动耦合精确地约束所有 6 个自由度。

9.2 滚动而不打滑

　　 在表面上滚动而不打滑的物体，其质心的速度等于其角速度与从接触点到质心的矢量的叉积:

对于不倾斜或不转动的对象，这简化为 $v = r\omega$。

9.3 不可拉伸的绳索

　　 这种情况下，物体由一根理想化的绳索连接，该绳索保持张紧状态，并且不能改变长度。约束是绳索所有段的长度之和是总长度，因此该和的时间导数为零。[21][22][23]这种类型的动力学问题是摆。另一个例子是，一个鼓在重力的牵引下，通过不可拉伸的绳索将落在轮辋上的重物旋转。[24]这种类型的平衡问题（即非运动学问题）是悬链线。[25]

9.4 运动副

　　 勒洛称形成机器运动对的组件之间的理想连接为运动副。他区分了据说在两个连杆之间具有线接触的较高对和在连杆之间具有面积接触的较低对。菲利普斯表明，有许多方法来构造不适合这种简单分类的对。[26]

　　 较低副

　　 较低对是理想的关节或完整约束，它保持移动实体(三维)中的点、线或平面与固定实体中相应的点画线或平面之间的接触。有以下几种情况:

• 转动副或铰接接头需要移动体中的线或轴保持与固定体中的线共线，并且移动体中垂直于该线的平面保持与固定体中类似垂直平面的接触。这给连杆的相对运动施加了五个约束，因此连杆具有一个自由度，即围绕铰链轴的纯旋转。
• 棱柱形接头或滑块要求移动体中的线或轴保持与固定体中的线共线，并且移动体中平行于该线的平面保持与固定体中类似平行平面的接触。这对连杆的相对运动施加了五个限制，因此连杆具有一个自由度。这个自由度是滑块沿线的距离。
• 圆柱形接头要求移动体中的线或轴保持与固定体中的线共线。它是转动关节和滑动关节的组合。这个关节有两个自由度。移动物体的位置由围绕轴的旋转和沿着轴的滑动来定义。
• 球形接头要求移动体中的一个点与固定体中的一个点保持接触。这个关节有三个自由度。
• 平面接头要求移动体中的平面与固定体中的平面保持接触。这个关节有三个自由度。

　　 较高副

　　 一般来说，较高的副是一个约束，要求移动体中的曲线或表面保持与固定体中的曲线或表面的接触。例如，凸轮与其从动件之间的接触是一个更高的副，称为凸轮关节。同样，构成两个齿轮啮合齿的渐开线曲线之间的接触也是凸轮关节。

9.5 运动链

　　 由运动副（“关节”）连接的刚体（“连杆”）称为运动链。机构和机器人是运动链的例子。通过使用移动公式计算关节的数目和关节的数目和类型来确定运动链的自由度。这个公式也可以用来枚举具有给定自由度的运动链的拓扑结构，这被称为机械设计中的类型综合。

　　 实例

　　 由 N 个连杆和 J 铰接或滑动关节组装的平面一自由度连杆机构为：

• N=2，j=1 :作为杠杆的两杆联动装置；
• N=4，j=4 :四连杆机构；
• N=6，j=7 :六连杆机构。这必须有两个链接（“三元链接”）来支持三个关节。有两种不同的拓扑结构，这取决于两个三元连杆是如何连接的。在瓦特拓扑中，这两个三元链路有一个公共连接；在斯蒂芬森拓扑中，这两个三元链路没有公共连接，并且通过二元链路连接。[27]
• N=8，j=10 :具有 16 种不同拓扑结构的八连杆机构；
• N=10，j=13 :具有 230 种不同拓扑结构的十杆连杆机构；
• N=12，j=16 :具有 6，856 种拓扑结构的十二连杆机构。

　　 对于较大的链及其连杆拓扑，请参见 R. P. Sunkari 和 L. C. Schmidt，“采用麦凯型算法进行平面运动链的结构综合”，机制和机器理论#41，1021–1030 页(2006)。

10. 参考文献

　　 [1] ^Edmund Taylor Whittaker (1904). A Treatise on the Analytical Dynamics of Particles and Rigid Bodies. Cambridge University Press. Chapter 1. ISBN 0-521-35883-3..

　　 [2] ^Joseph Stiles Beggs (1983). Kinematics. Taylor & Francis. p. 1. ISBN 0-89116-355-7..

　　 [3] ^Thomas Wallace Wright (1896). Elements of Mechanics Including Kinematics, Kinetics and Statics. E and FN Spon. Chapter 1..

　　 [4] ^Russell C. Hibbeler (2009). "Kinematics and kinetics of a particle". Engineering Mechanics: Dynamics (12th ed.). Prentice Hall. p. 298. ISBN 0-13-607791-9..

　　 [5] ^Ahmed A. Shabana (2003). "Reference kinematics". Dynamics of Multibody Systems (2nd ed.). Cambridge University Press. ISBN 978-0-521-54411-5..

　　 [6] ^P. P. Teodorescu (2007). "Kinematics". Mechanical Systems, Classical Models: Particle Mechanics. Springer. p. 287. ISBN 1-4020-5441-6.。.

　　 [7] ^A. Biewener (2003). Animal Locomotion. Oxford University Press. ISBN 019850022X..

　　 [8] ^J.M. McCarthy 和 G. S. Soh，2010 年，连杆的几何设计，纽约斯普林格。.

　　 [9] ^Ampère, André-Marie. Essai sur la Philosophie des Sciences. Chez Bachelier..

　　 [10] ^Merz, John (1903). A History of European Thought in the Nineteenth Century. Blackwood, London. p. 5..

　　 [11] ^O. Bottema & B. Roth (1990). Theoretical Kinematics. Dover Publications. preface, p. 5. ISBN 0-486-66346-9..

　　 [12] ^Harper, Douglas. "cinema". Online Etymology Dictionary..

　　 [13] ^https://web.archive.org/web/20221025164404/https://www.youtube.com/watch?v=jLJLXka2wEM 速成物理.

　　 [14] ^https://web.archive.org/web/20221025164404/https://www.youtube.com/watch?v=jLJLXka2wEM 速成物理积分.

　　 [15] ^https://web.archive.org/web/20221025164404/https://duckduckgo.com/?q =面积+的+a+矩形& ampatb=v92-4_g&。ia DuckDuckGo.

　　 [16] ^https://web.archive.org/web/20221025164404/http://www . mathsisfun . com/代数/trig-area-triangle-with-not-right-angle . html 没有直角的三角形面积.

　　 [17] ^https://web.archive.org/web/20221025164404/https://www 4 . uwsp . edu/phys tar/kmen ning/phys 203/eqs/运动学. gif.

　　 [18] ^几何学:对给定元素在特定变换下保持不变的性质的研究。"Definition of geometry". Merriam-Webster on-line dictionary..

　　 [19] ^Paul, Richard (1981). Robot manipulators: mathematics, programming, and control : the computer control of robot manipulators. MIT Press, Cambridge, MA. ISBN 978-0-262-16082-7..

　　 [20] ^R. Douglas Gregory (2006). Chapter 16. Cambridge, England: Cambridge University. ISBN 0-521-82678-0..

　　 [21] ^William Thomson Kelvin & Peter Guthrie Tait (1894). Elements of Natural Philosophy. Cambridge University Press. p. 4. ISBN 1-57392-984-0..

　　 [22] ^William Thomson Kelvin & Peter Guthrie Tait (1894). Elements of Natural Philosophy. p. 296..

　　 [23] ^M. Fogiel (1980). "Problem 17-11". The Mechanics Problem Solver. Research & Education Association. p. 613. ISBN 0-87891-519-2..

　　 [24] ^Irving Porter Church (1908). Mechanics of Engineering. Wiley. p. 111. ISBN 1-110-36527-6..

　　 [25] ^Morris Kline (1990). Mathematical Thought from Ancient to Modern Times. Oxford University Press. p. 472. ISBN 0-19-506136-5..

　　 [26] ^Phillips, Jack (2007). Freedom in Machinery, Volumes 1–2 (reprint ed.). Cambridge University Press. ISBN 978-0-521-67331-0..

　　 [27] ^Tsai, Lung-Wen (2001). Mechanism design:enumeration of kinematic structures according to function (llustrated ed.). CRC Press. p. 121. ISBN 978-0-8493-0901-4..