集合论(综述)
贡献者: 待更新
本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。
集合论是数学逻辑的一个分支,研究集合,集合可以非正式地描述为对象的集合。尽管任何类型的对象都可以组成一个集合,但集合论——作为数学的一个分支——主要关注那些与整个数学相关的集合。
现代集合论的研究始于 19 世纪 70 年代,由德国数学家理查德·德德金德和乔治·康托尔发起。特别是,乔治·康托尔通常被认为是集合论的创始人。在这个早期阶段研究的非形式化系统被称为朴素集合论。在朴素集合论中发现悖论(如罗素悖论、康托尔悖论和布拉利-福尔蒂悖论)之后,20 世纪初提出了各种公理化系统,其中泽梅洛–弗兰克尔集合论(无论是否包含选择公理)仍然是最著名和最研究的。
集合论通常被用作整个数学的基础系统,特别是以泽梅洛–弗兰克尔集合论与选择公理的形式。除了其基础性作用外,集合论还提供了一个框架,用于发展数学中的无穷大理论,并在计算机科学(如关系代数理论)、哲学、形式语义学和进化动力学等领域有着广泛的应用。它的基础性吸引力、与悖论的关系、以及对无穷大的概念及其多重应用的影响,使得集合论成为逻辑学家和数学哲学家关注的主要领域之一。当代集合论的研究涵盖了广泛的主题,从实数线的结构到大基数的一致性研究。
1. 历史
早期历史
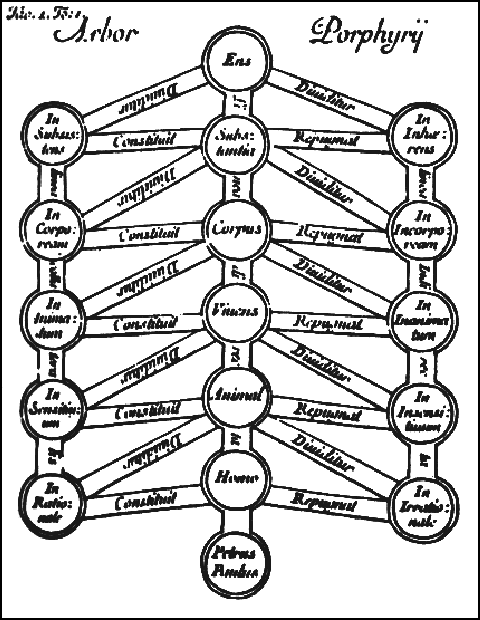
基本的对象分组概念自至少在数字的出现以来就已存在,而将集合视为自身对象的概念至少自公元 3 世纪的《波尔斐里树》以来就存在。集合的简单性和普遍性使得很难确定现在在数学中使用的集合的起源,然而,伯纳德·博尔扎诺的《无穷悖论》(*Paradoxien des Unendlichen*,1851 年)通常被认为是集合首次严格引入数学的工作。在他的著作中,他(除了其他内容外)扩展了伽利略的悖论,并引入了无限集合的一对一对应,例如通过关系 $5y = 12x$,在区间 $[0, 5]$ 和 $[0, 12]$ 之间建立了对应。然而,他拒绝称这些集合是等势的,他的工作通常被认为在他那个时代的数学中没有产生影响。\(^\text{[1][2]}\)
在数学集合论出现之前,无穷的基本概念被认为完全属于哲学领域(参见:无穷(哲学)和无穷 § 历史)。自公元前 5 世纪起,从西方的希腊哲学家芝诺开始(以及东方的早期印度数学家),数学家们就一直在与无穷的概念作斗争。随着 17 世纪末微积分的发展,哲学家们开始普遍区分实际无穷与潜在无穷,其中数学仅涉及后者。\(^\text{[3]}\) 卡尔·弗里德里希·高斯 famously 说道:“无穷不过是一个修辞,帮助我们讨论极限。完成的无穷这一概念不属于数学。”\(^\text{[4]}\)
数学集合论的发展受到了几位数学家的启发。伯恩哈德·黎曼在《几何基础上的假设》(1854 年)的讲座中提出了关于拓扑学的新思想,并关于将数学(特别是几何学)建立在集合或流形的基础上,以类的方式(他称之为 Mannigfaltigkeit),这现在被称为点集拓扑学。该讲座于 1868 年由理查德·德德金德出版,同时也出版了黎曼关于三角级数的论文(该论文提出了黎曼积分),后者成为实分析领域中研究 “严肃的” 不连续函数的起点。年轻的乔治·康托尔进入了这一领域,这引导他研究点集。大约在 1871 年,受黎曼的影响,德德金德开始在他的出版物中使用集合,这些出版物非常清晰和精确地处理了等价关系、集合的划分和同态。由此,20 世纪数学中许多常见的集合论程序可以追溯到他的工作。然而,他直到 1888 年才出版了关于集合论的正式解释。
朴素集合论
集合论,现代数学家所理解的集合论,通常被认为是由乔治·康托尔于 1874 年发表的论文《关于所有实代数数集合的一个性质》奠定的基础。\(^\text{[5][6][7]}\) 在这篇论文中,他发展了基数的概念,通过一一对应来比较两个集合的大小。他的 “革命性发现” 是,所有实数的集合是不可数的,也就是说,不能将所有实数列在一张列表中。这个定理是通过康托尔的第一次不可数性证明来证明的,这与更为人熟知的使用对角线法的证明有所不同。
康托尔引入了集合论中的基本构造,如集合 $A$ 的幂集,它是 $A$ 的所有可能子集的集合。他后来证明,幂集 $A$ 的大小严格大于 $A$ 的大小,即使 $A$ 是一个无限集合;这一结果很快被称为康托尔定理。康托尔发展了一种超限数的理论,称为基数和序数,扩展了自然数的算术。他为基数使用的符号是希伯来字母 $\aleph$(ℵ,aleph)带有自然数下标;对于序数,他使用希腊字母 $\omega$(ω,omega)。
集合论开始成为新 “现代” 数学方法的一个重要组成部分。最初,康托尔的超限数理论被认为是违反直觉的——甚至是令人震惊的。这导致它遭遇了数学当代人物如利奥波德·克罗内克和亨利·庞加莱的反对,后来也遭遇了赫尔曼·韦尔和 L·E·J·布劳威尔的抵制,而路德维希·维特根斯坦提出了哲学上的异议(参见:康托尔理论的争议)。\(^\text{[a]}\) 德德金德的代数风格直到 1890 年代才开始找到追随者。
尽管存在争议,康托尔的集合论在 20 世纪初得到了显著的发展,得益于几位著名数学家和哲学家的贡献。理查德·德德金德在同一时期开始在他的出版物中使用集合,并以著名的德德金德切割法构造实数。他还与朱塞佩·皮亚诺合作,发展了皮亚诺公理,这些公理使用集合论的思想形式化了自然数算术,并引入了用于集合成员关系的 epsilon 符号。可能最为重要的是,戈特洛布·弗雷格开始发展他的《算术基础》。
在他的著作中,弗雷格试图通过逻辑公理来构建所有数学,使用康托尔的基数概念。例如,“马棚里有四匹马” 这句话意味着四个对象属于 “马” 这一概念。弗雷格尝试通过基数(“...的数量”,或 $Nx: Fx$)来解释我们对数字的理解,依赖于休谟原则。
然而,弗雷格的工作很短命,因为伯特兰·罗素发现他的公理导致了一个矛盾。具体而言,弗雷格的基本法则 V(现在被称为无限制理解公理模式)。根据基本法则 V,对于任何足够明确的属性,都存在一个集合,包含所有且仅有具备该属性的对象。矛盾,称为罗素悖论,证明过程如下:
令 $R$ 为所有不包含自身的集合的集合(这个集合有时被称为 “罗素集合”)。如果 $R$ 不是它自己的成员,那么它的定义意味着它是它自己的成员;然而,如果它是它自己的成员,那么它就不是它自己的成员,因为它是所有不包含自身的集合的集合。由此产生的矛盾就是罗素悖论。用符号表示:
令 $R = \{x \mid x \notin x\}$,那么 $R \in R \iff R \notin R$
这出现在多个悖论或违反直觉的结果发生的时期。例如,平行公理无法被证明,存在无法计算或明确描述的数学对象,存在无法通过皮亚诺算术证明的算术定理。其结果是数学的基础危机。
2. 基本概念和符号
集合论始于对象 $o$ 与集合 $A$ 之间的基本二元关系。如果 $o$ 是 $A$ 的成员(或元素),则使用符号 $o \in A$。集合通过列出以逗号分隔的元素,或通过其元素的特征属性,在大括号{ }内描述。\(^\text{[8]}\) 由于集合是对象,成员关系也可以涉及集合本身,即集合本身可以是其他集合的成员。
两个集合之间的一个派生二元关系是子集关系,也叫集合包含。如果集合 $A$ 的所有成员也是集合 $B$ 的成员,则 $A$ 是 $B$ 的子集,记作 $A \subseteq B$。例如,$\{1, 2\}$ 是 $\{1, 2, 3\}$ 的子集,$\{2\}$ 也是,但 $\{1, 4\}$ 不是。根据这一定义,集合是它自己的子集。对于不适用或应当排除这种可能性的情况,定义了真子集,通常记作 $A \subset B$、$A \subsetneq B$,或 $A \subsetneqq B$(但请注意,符号 $A \subset B$ 有时与 $A \subseteq B$ 同义使用;即允许 $A$ 和 $B$ 相等的可能性)。我们称 $A$ 是 $B$ 的真子集,当且仅当 $A$ 是 $B$ 的子集,但 $A$ 不等于 $B$。此外,1、2 和 3 是集合 $\{1, 2, 3\}$ 的成员(元素),但不是它的子集;反过来,像 $\{1\}$ 这样的子集不是集合 $\{1, 2, 3\}$ 的成员。更复杂的关系也可以存在;例如,集合 $\{1\}$ 既是集合 $\{1, {1}\}$ 的成员,也是其真子集。
正如算术包含对数字的二元运算,集合论也包含对集合的二元运算。\(^\text{[9]}\) 以下是它们的一部分:
- 集合 A 和 B 的并集,记作 $A \cup B$,是所有属于 A、B 或两者的对象的集合。\(^\text{[10]}\) 例如,集合 $\{1, 2, 3\}$ 和 $\{2, 3, 4\}$ 的并集是集合 $\{1, 2, 3, 4\}$。
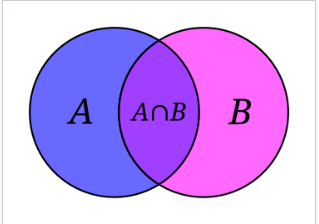
- 集合 A 和 B 的交集,记作 $A \cap B$,是所有同时属于 A 和 B 的对象的集合。\(^\text{[11]}\) 例如,集合 $\{1, 2, 3\}$ 和 $\{2, 3, 4\}$ 的交集是集合 $\{2, 3\}$。
- 集合 U 和 A 的差集,记作 $U \setminus A$,是所有属于 U 但不属于 A 的对象的集合。\(^\text{[12]}\) 例如,集合 $\{1, 2, 3\} \setminus \{2, 3, 4\}$ 是集合 $\{1\}$,而反过来,集合 $\{2, 3, 4\} \setminus \{1, 2, 3\}$ 是集合 $\{4\}$。当 $A$ 是 $U$ 的子集时,差集 $U \setminus A$ 也称为 A 在 U 中的补集。在这种情况下,如果 $U$ 的选择在上下文中是明确的,有时使用符号 $A^c$ 代替 $U \setminus A$,特别是如果 $U$ 是全集,如在维恩图的研究中。\(^\text{[13]}\)
- 集合 A 和 B 的对称差,记作 $A \triangle B$ 或 $A \ominus B$,是所有只属于 A 或 B 其中一个集合的对象的集合(即属于其中一个集合但不属于两个集合的元素)。例如,集合 $\{1, 2, 3\}$ 和 $\{2, 3, 4\}$ 的对称差是集合 $\{1, 4\}$。它是并集与交集的差集,$(A \cup B) \setminus (A \cap B)$ 或 $(A \setminus B) \cup (B \setminus A)$。
- 集合 A 和 B 的笛卡尔积,记作 $A \times B$,是所有可能的有序对 $(a, b)$ 的集合,其中 $a$ 是 A 的成员,$b$ 是 B 的成员。例如,集合 $\{1, 2\}$ 和 $\{\text{red}, \text{white}\}$ 的笛卡尔积是 $\{(1, \text{red}), (1, \text{white}), (2, \text{red}), (2, \text{white})\}$。\(^\text{[14]}\)
一些基本的集合,具有重要的中心地位,包括自然数集合、实数集合和空集合——唯一一个不包含任何元素的集合。空集合有时也被称为零集合,[15] 虽然这个名称是模糊的,可能导致多种解释。空集合可以用空的大括号表示 $\{\}$,也可以用符号 $\varnothing$ 或 $\emptyset$ 表示。
集合 $A$ 的幂集,记作 ${\mathcal {P}}(A)$,是一个集合,其中的成员是 $A$ 的所有可能子集。例如,集合 $\{1, 2\}$ 的幂集是 $\{\{\}, \{1\}, \{2\}, \{1, 2\}\}$。值得注意的是,${\mathcal {P}}(A)$ 包含了 $A$ 本身和空集合。
3. 本体论
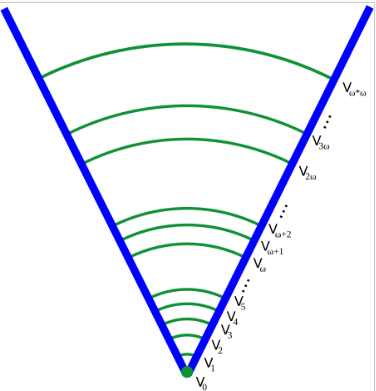
如果一个集合的所有成员都是集合,并且它的成员的成员也是集合,依此类推,那么这个集合就是纯集合。例如,仅包含空集合的集合是一个非空的纯集合。在现代集合论中,通常将注意力限制在冯·诺依曼纯集合宇宙中,许多公理化集合论系统旨在仅公理化纯集合。这个限制有许多技术上的优点,并且几乎没有失去一般性,因为本质上所有数学概念都可以通过纯集合来建模。冯·诺依曼宇宙中的集合被组织成一个累积层次结构,基于它们的成员、成员的成员等的嵌套深度。这个层次结构中的每个集合通过超限递归被分配一个序数 $\alpha$,称为它的秩。纯集合 $X$ 的秩被定义为严格大于其任何元素的秩的最小序数。例如,空集合被分配秩 0,而仅包含空集合的集合被分配秩 1。对于每个序数 $\alpha$,集合 $V_{\alpha}$ 被定义为包含所有秩小于 $\alpha$ 的纯集合的集合。整个冯·诺依曼宇宙用 $V$ 表示。
4. 形式化集合论
基础集合论可以通过非正式和直观的方式进行研究,因此可以使用维恩图在小学进行教学。直观方法默认为一个集合可以由满足某一特定定义条件的所有对象的类组成。这一假设导致了悖论,其中最简单且最著名的是罗素悖论和布拉利-福尔蒂悖论。公理化集合论最初是为了将集合论中的这些悖论去除而设计的。\(^\text{[注 1]}\)
最广泛研究的公理化集合论系统意味着所有集合构成一个累积层次结构。\(^\text{[b]}\) 这些系统有两种类型,分别是:
- 仅包含集合的系统。这包括最常见的公理化集合论——泽梅洛–弗兰克尔集合论(ZFC),以及 ZFC 的片段,包括:
- 泽梅洛集合论,它将替代公理模式替换为分离公理模式;
- 一般集合论,泽梅洛集合论的一个小片段,足以支持皮亚诺公理和有限集合;
- 克里普克-普拉特集合论,它省略了无限公理、幂集公理和选择公理,并弱化了分离公理和替代公理模式。
- 集合与真类的系统。这些系统包括冯·诺依曼-伯奈-哥德尔集合论,它与 ZFC 在关于集合的定理方面具有相同的强度;以及莫尔斯-凯利集合论和塔尔斯基-格罗腾迪克集合论,它们都比 ZFC 更强
。 上述系统可以被修改以允许原始元素,这些对象可以是集合的成员,但它们本身不是集合,也没有任何成员。
由威拉德·范·奥曼·奎因(Willard Van Orman Quine)提出的新基础(New Foundations,NF)系统(包括允许原始元素的 NFU 和不包含原始元素的 NF)并不基于累积层次结构。NF 和 NFU 包括一个 “所有集合的集合”,相对于这个集合,每个集合都有一个补集。在这些系统中,原始元素是重要的,因为 NF(而非 NFU)会产生不满足选择公理的集合。尽管 NF 的本体论不反映传统的累积层次结构,并且违反了良基础性,托马斯·福斯特认为它确实反映了集合的迭代观念。\(^\text{[16]}\)
构造性集合论系统,如 CST、CZF 和 IZF,将它们的集合公理嵌入直觉逻辑中,而不是经典逻辑。还有一些系统接受经典逻辑,但具有非标准的成员关系。这些系统包括粗集理论和模糊集理论,其中体现成员关系的原子公式的值不仅仅是 “真” 或 “假”。ZFC 的布尔值模型是一个相关的主题。
Edward Nelson 在 1977 年提出了一种 ZFC 的扩展,称为内部集合论。\(^\text{[17]}\)
应用
许多数学概念可以仅通过集合论的概念精确定义。例如,图、流形、环、向量空间和关系代数等多种数学结构都可以定义为满足各种(公理化)性质的集合。等价关系和顺序关系在数学中无处不在,数学关系的理论可以用集合论来描述。\(^\text{[18][19]}\)
集合论也是许多数学领域的有前景的基础系统。自《数学原理》第一卷出版以来,人们声称大多数(甚至所有)数学定理都可以使用恰当设计的集合论公理集来推导,并通过许多定义加以补充,使用一阶或二阶逻辑。例如,自然数和实数的性质可以在集合论中推导,因为每个数系都可以通过将其元素表示为特定形式的集合来定义。\(^\text{[20]}\)
集合论作为数学分析、拓扑学、抽象代数和离散数学的基础也是不具争议的;数学家们(原则上)接受这些领域的定理可以从相关定义和集合论的公理中推导出来。然而,至今为止,从集合论中正式验证的复杂数学定理的完整推导仍然很少,因为这样的形式化推导通常比数学家常用的自然语言证明要长得多。一个验证项目——Metamath,包含了从 ZFC 集合论、一阶逻辑和命题逻辑出发,通过人工编写并计算机验证的超过 12,000 个定理的推导。[21]
5. 研究领域
集合论是数学的一个主要研究领域,具有许多相互关联的子领域:
组合集合论
组合集合论涉及有限组合学向无限集合的扩展。这包括基数算术的研究和拉姆齐定理的扩展研究,例如埃尔德什–拉多定理的研究。
描述集合论
描述集合论是研究实数线的子集,更一般地,是研究波兰空间的子集。它从研究 Borel 层次中的点类开始,并扩展到更复杂层次的研究,例如投影层次和瓦奇层次。许多 Borel 集合的性质可以在 ZFC 中建立,但证明这些性质对更复杂的集合成立需要额外的公理,这些公理与确定性和大基数相关。
有效描述集合论是集合论和递归理论之间的领域。它包括研究轻面点类,并与超算术理论密切相关。在许多情况下,经典描述集合论的结果都有有效的版本;在某些情况下,通过首先证明有效版本,然后扩展(“相对化”)它,使其更广泛适用,从而获得新的结果。 最近的研究领域涉及 Borel 等价关系和更复杂的可定义等价关系。这对许多数学领域中不变量的研究具有重要应用。
模糊集合论
在康托尔定义并泽梅洛和弗兰克尔公理化的集合论中,一个对象要么是集合的成员,要么不是。在模糊集合论中,这一条件被 Lotfi A. Zadeh 放宽,使得一个对象在集合中有一个成员度,即一个介于 0 和 1 之间的数字。例如,一个人属于 “高个子” 集合的成员度比简单的是或否的回答更为灵活,可以是一个实数,例如 0.75。
内模型理论
泽梅洛–弗兰克尔集合论(ZF)的内模型是一个传递类,它包含所有序数并满足 ZF 的所有公理。典型的例子是哥德尔发展出的构造宇宙 L。研究内模型之所以重要,是因为它可以用来证明一致性结果。例如,可以证明无论 ZF 的一个模型 $V$ 是否满足连续统假设或选择公理,原始模型内部构造的内模型 $L$ 将同时满足广义连续统假设和选择公理。因此,假设 ZF 是一致的(至少有一个模型)意味着 ZF 与这两个公理一起是一致的。
内模型的研究在确定性和大基数的研究中很常见,特别是在考虑如确定性公理这样的公理时,这些公理与选择公理相矛盾。即使一个固定的集合论模型满足选择公理,内模型也可能不满足选择公理。例如,足够大的基数的存在意味着存在一个内模型,满足确定性公理(因此不满足选择公理)。\(^\text{[22]}\)
大基数
大基数是具有额外属性的基数。研究了许多这样的属性,包括不可达基数、可测基数等。这些属性通常意味着该基数必须非常大,具有指定属性的基数的存在在泽梅洛–弗兰克尔集合论中是无法证明的。
确定性
确定性指的是,在适当的假设下,某些完美信息的二人游戏从一开始就已决定,即一个玩家必须拥有获胜策略。这些策略的存在在描述集合论中具有重要意义,因为假设一个更广泛类别的游戏是确定的,通常意味着一个更广泛类别的集合将具有拓扑性质。确定性公理(AD)是一个重要的研究对象;尽管与选择公理不兼容,AD 意味着所有实数线的子集行为良好(特别是可测并具有完美集性质)。AD 可以用来证明瓦奇度数具有优雅的结构。
强制法
保罗·科恩在寻找一个 ZF 模型,使得连续统假设失败,或者一个 ZF 模型,使得选择公理失败时,发明了强制法。强制法向某个给定的集合论模型中加入额外的集合,从而创建一个具有由构造和原始模型确定(即 “强制”)性质的更大模型。例如,科恩的构造方法向自然数的子集添加额外的子集,而不改变原始模型的任何基数。强制法也是通过有限方法证明相对一致性的两种方法之一,另一种方法是布尔值模型。
基数不变量
基数不变量是通过基数来度量的实数线的一个性质。例如,一个经过充分研究的不变量是那些其并集为整个实数线的稀疏集合的集合的最小基数。这些是基数不变量,因为任何两个同构的集合论模型在每个不变量上必须给出相同的基数。许多基数不变量已经被研究,它们之间的关系通常是复杂的,并且与集合论的公理相关。
集合论拓扑学
集合论拓扑学研究那些在本质上是集合论性质的问题,或需要高级集合论方法来解决的一般拓扑问题。这些定理中的许多是 ZFC 独立的,需要更强的公理来证明。一个著名的问题是正常摩尔空间问题,这是一个一般拓扑中的问题,曾是激烈研究的主题。最终,正常摩尔空间问题的答案被证明是 ZFC 独立的。
6. 争议
从集合论的起源开始,一些数学家就反对它作为数学的基础。最常见的反对意见是由克罗内克在集合论的最初几年提出的,他从构造主义的观点出发,认为数学与计算密切相关。如果这个观点被接受,那么在朴素集合论和公理化集合论中对无限集合的处理,就会将不可计算的方法和对象引入到数学中,甚至在原则上也是不可计算的。构造主义作为数学替代基础的可行性在埃雷特·毕晓普的影响力巨大的《构造分析基础》一书中得到了极大的增强。\(^\text{[23]}\)
另一种由亨利·庞加莱提出的反对意见是,使用分离公理模式和替代公理模式以及幂集公理来定义集合,向数学对象的定义中引入了自指性(即一种循环性)。尽管依赖自指性基础的数学的范围比常见的泽梅洛–弗兰克尔理论小,但它的范围远大于构造数学,甚至以至于所罗门·费弗曼曾说过:“所有科学上适用的分析都可以通过[使用自指方法]来发展。”\(^\text{[24]}\)
路德维希·维特根斯坦从哲学角度批判了集合论,认为它具有数学柏拉图主义的含义。\(^\text{[25]}\) 他写道:“集合论是错误的”,因为它建立在 “虚构符号的胡说八道” 之上,具有 “有害的语言习惯”,并且谈论 “所有数字” 是荒谬的。\(^\text{[26]}\) 维特根斯坦将数学与算法推理相提并论;\(^\text{[27]}\) 对他来说,数学需要一个稳固基础的观点显得荒谬。\(^\text{[28]}\) 此外,由于人类努力本质上是有限的,维特根斯坦的哲学要求对激进的构造主义和有限主义做出本体论承诺。元数学陈述——对维特根斯坦来说,包括任何涉及无限领域的量化陈述,因此几乎所有现代集合论——都不是数学。\(^\text{[29]}\) 在《数学基础的评论》中,维特根斯坦试图反驳哥德尔的不完备定理,但仅阅读了摘要后就作出结论,这导致了他的一次巨大错误。如评论家克雷泽尔、伯奈、达梅特和古德斯坦所指出的,他的许多批评并不适用于这篇论文。直到最近,像克里斯平·赖特这样的哲学家才开始重新评价维特根斯坦的论点。\(^\text{[30]}\)
范畴论学者提出了拓扑理论作为传统公理化集合论的替代方案。拓扑理论可以解释该理论的各种替代方案,例如构造主义、有限集合论和可计算集合论。\(^\text{[31][32]}\) 拓扑空间还为强制法和选择公理与 ZF 的独立性讨论提供了自然的背景,并为无点拓扑和斯通空间提供了框架。\(^\text{[33]}\)
一个活跃的研究领域是单值基础及与之相关的同伦类型理论。在同伦类型理论中,集合可以被视为同伦 0 类型,集合的普遍属性来源于更高归纳类型的归纳和递归性质。像选择公理和排中律这样的原则可以以一种与集合论中经典表述相对应的方式进行表述,或者以类型理论中独特的方式表述。这些原则中的一些可能被证明是其他原则的结果。这些公理原则的多样化表述为详细分析推导各种数学结果所需的表述提供了可能。\(^\text{[34][35]}\)
7. 数学教育
随着集合论作为现代数学基础的流行,支持在数学教育早期引入朴素集合论基础的观点也逐渐增加。
在美国,1960 年代的新数学实验旨在将基础集合论等抽象概念教授给小学生,但遭遇了大量批评。\(^\text{[36]}\) 欧洲学校的数学课程也沿袭了这一趋势,目前在所有年级中都包含了这一学科。维恩图广泛应用于向小学生解释基本的集合论关系(尽管约翰·维恩最初将其设计为评估术语逻辑推理有效性的一部分)。
集合论被用来向学生介绍逻辑运算符(NOT、AND、OR),以及集合的语义或规则描述(从技术上讲是内涵定义)\(^\text{[37]}\)(例如,“以字母 A 开头的月份”),这在学习计算机编程时可能会有所帮助,因为布尔逻辑在各种编程语言中都有应用。同样,集合和其他类似集合的对象,如多重集合和列表,是计算机科学和编程中常见的数据类型。\(^\text{[38]}\)
此外,某些集合通常用于数学教学中,如自然数集合 $\mathbb{N}$、整数集合 $\mathbb{Z}$、实数集合 $\mathbb{R}$ 等。这些集合通常用于将数学函数定义为从一个集合(定义域)到另一个集合(值域)的关系。\(^\text{[39]}\)
8. 参见
- 集合论术语表
- 类(集合论)
- 集合论主题列表
- 关系模型 – 借鉴集合论
- 维恩图
- 集合范畴的初等理论
- 结构集合论
9. 注释
1.在他 1925 年的论文《集合论的公理化》中,约翰·冯·诺依曼观察到,“集合论的第一种‘朴素’版本,由康托尔提出,导致了矛盾。这些就是著名的悖论,如不包含自身的所有集合的集合(罗素悖论)、所有超限序数的集合(布拉利-福尔蒂悖论)以及所有有限可定义实数的集合(理查德悖论)。” 他接着指出,有两个 “倾向” 试图 “恢复” 集合论。对于第一个努力,代表人物有伯特兰·罗素、尤利乌斯·科尼希、赫尔曼·韦尔和 L·E·J·布劳威尔,冯·诺依曼称他们活动的 “总体效果……是毁灭性的”。至于第二组由泽梅洛、弗兰克尔和舍恩弗利斯组成的公理化方法,冯·诺依曼担心:“我们看到的只是导致悖论的已知推理模式失败了,但谁知道哪里没有其他推理模式呢?” 因此,他开始着手,"在第二组的精神下",通过 “有限数量的纯形式操作……产生我们希望看到的所有集合”,但不允许悖论的出现。(所有引用来自冯·诺依曼 1925 年的论文,转载自 van Heijenoort, Jean(1967 年,1976 年第三版),*从弗雷格到哥德尔:数学逻辑的文献,1879–1931*,哈佛大学出版社,剑桥,MA,ISBN 0-674-32449-8(平装版)。有关历史的概述,可以在冯·诺依曼 1925 年论文之前的评论中找到,作者为 van Heijenoort。)
a.对康托尔工作的反对有时非常激烈:利奥波德·克罗内克的公开反对和人身攻击包括将康托尔称为 “科学江湖医生”、“叛徒” 和 “腐化青年”。克罗内克反对康托尔证明代数数是可数的,以及超越数是不可数的,这些结果现在已被纳入标准数学课程。维特根斯坦在康托尔去世数十年后写道,数学 “充斥着集合论的有害语言习惯”,他将其视为 “彻头彻尾的胡说八道”,“可笑” 且 “错误”。
b.这对于 ZFC 是相反的;$V$ 是 ZFC 的一个模型。
10. 引用
- Ferreirós, José (2024), "集合论的早期发展",收录于 Zalta, Edward N.; Nodelman, Uri(编),*斯坦福哲学百科全书*(2024 年冬季版),形而上学研究实验室,斯坦福大学,原文存档于 2023-03-20,检索于 2025-01-04
- Bolzano, Bernard (1975),Berg, Jan(编),*《大小学引论与一般大小学的初步概念》*,伯纳德·博尔扎诺全集,编辑:Eduard Winter 等,第 II 卷,A 部分,第 7 页,斯图加特,巴德坎斯塔特:Friedrich Frommann Verlag 出版社,第 152 页,ISBN 3-7728-0466-7
- Zenkin, Alexander (2004),"实际无穷的逻辑与 G.康托尔关于连续统不可数性的对角线证明",*现代逻辑评论*,第 9 卷,第 30 期,第 27–80 页,原文存档于 2020-09-22,检索于 2025-01-04
- Dunham, William (1991),*天才之旅:数学的伟大定理*,企鹅出版社,第 254 页,ISBN 9780140147391
- Cantor, Georg (1874),"Ueber eine Eigenschaft des Inbegriffes aller reellen algebraischen Zahlen",*《纯粹与应用数学杂志》*(德文),1874 年第 77 期:258–262,doi:10.1515/crll.1874.77.258,S2CID 199545885,原文存档于 2012-06-04,检索于 2013-01-31
- Johnson, Philip (1972),*集合论的历史*,Prindle, Weber & Schmidt 出版社,ISBN 0-87150-154-6
- Dauben, Joseph (1979),*乔治·康托尔:他的数学与无限的哲学*,哈佛大学出版社,第 30–54 页,ISBN 0-674-34871-0
- "Introduction to Sets",www.mathsisfun.com,原文存档于 2006-07-16,检索于 2020-08-20
- Kolmogorov, A.N.; Fomin, S.V. (1970),*初级实分析*(修订版英文版),纽约:Dover Publications 出版社,第 2–3 页,ISBN 0486612260,OCLC 1527264
- "集合论 | 基础、示例和公式",*大英百科全书*,原文存档于 2020-08-20,检索于 2020-08-20
- Kaplansky, Irving (1972),De Prima, Charles(编),*集合论与度量空间*,波士顿:Allyn and Bacon 出版社,第 4 页
- Kaplansky, Irving (1972),De Prima, Charles(编),*集合论与度量空间*,波士顿:Allyn and Bacon 出版社,第 5–6 页
- Kaplansky, Irving (1972),De Prima, Charles(编),*集合论与度量空间*,波士顿:Allyn and Bacon 出版社,第 5–6 页
- Kaplansky, Irving (1972),De Prima, Charles(编),*集合论与度量空间*,波士顿:Allyn and Bacon 出版社,第 19 页
- Bagaria, Joan (2020),"集合论",收录于 Zalta, Edward N.(编),*斯坦福哲学百科全书*(2020 年春季版),形而上学研究实验室,斯坦福大学,检索于 2020-08-20
- Forster, T. E. (2008),"集合的迭代观念"(PDF),*符号逻辑评论*,第 1 卷,第 97–110 页,doi:10.1017/S1755020308080064,S2CID 15231169
- Nelson, Edward (1977 年 11 月),"内部集合论:一种非标准分析的新方法",*美国数学学会公报*,第 83 卷,第 6 期:1165,doi:10.1090/S0002-9904-1977-14398-X
- "6.3: 等价关系和划分",*数学 LibreTexts*,2019-11-25,原文存档于 2022-08-16,检索于 2022-07-27
- "顺序关系和函数"(PDF),Web.stanford.edu,原文存档(PDF)于 2022-07-27,检索于 2022-07-29
- Mendelson, Elliott (1973),*数系与分析基础*,Academic Press 出版社,MR 0357694,Zbl 0268.26001
- "集合论中的划分计算"(PDF),Ams.org,检索于 2022-07-29
- Jech, Thomas (2003),*集合论*,Springer 数学单刊(第三千年版),柏林,纽约:Springer-Verlag 出版社,第 642 页,ISBN 978-3-540-44085-7,Zbl 1007.03002
- Bishop, Errett (1967),*构造分析基础*,纽约:Academic Press 出版社,ISBN 4-87187-714-0
- Feferman, Solomon (1998),*在逻辑的光辉下*,纽约:牛津大学出版社,第 280–283 页,293–294 页,ISBN 0-195-08030-0
- Rodych, Victor (2018 年 1 月 31 日),"维特根斯坦的数学哲学",收录于 Zalta, Edward N.(编),*斯坦福哲学百科全书*(2018 年春季版)
- Wittgenstein, Ludwig (1975),*哲学笔记*,§129,§174,牛津:Basil Blackwell 出版社,ISBN 0-631-19130-5
- Rodych 2018,§2.1:“当我们证明一个定理或决定一个命题时,我们是以纯粹形式化的、句法的方式操作的。在进行数学时,我们并不是发现‘已经存在的真理’(PG 481)——我们是逐步发明数学。” 然而,值得注意的是,维特根斯坦并没有将这种推理与哲学逻辑等同起来;参见 Rodych §1,第 7-12 段。
- Rodych 2018,§3.4:“鉴于数学是‘一堆证明技巧’(RFM III,§46),它不需要基础(RFM VII,§16),也无法给出一个不言自明的基础(PR §160;WVC 34 & 62;RFM IV,§3)。由于集合论是为了给数学提供基础而发明的,因此,它至少是不必要的。”
- Rodych 2018,§2.2:“一个量化无限领域的表达式永远不是一个有意义的命题,即使我们已经证明了,例如,某个特定的数字 $n$ 具有某个特定的属性。”
- Rodych 2018,§3.6。
- Ferro, Alfredo; Omodeo, Eugenio G.; Schwartz, Jacob T. (1980 年 9 月),"集合论的初等子语言的决策程序。I. 多层次三段论及一些扩展",*纯粹与应用数学通讯*,第 33 卷,第 5 期:599–608,doi:10.1002/cpa.3160330503
- Cantone, Domenico; Ferro, Alfredo; Omodeo, Eugenio G. (1989),*可计算集合论*,计算机科学国际专著系列,牛津科学出版,英国牛津:Clarendon Press 出版社,第 xii 页,347 页,ISBN 0-198-53807-3
- Mac Lane, Saunders; Moerdijk, Ieke (1992),*几何与逻辑中的层:拓扑理论的入门*,Springer-Verlag 出版社,ISBN 978-0-387-97710-2
- nLab 上的同伦类型理论
- *同伦类型理论:数学的单值基础*,原文存档于 2021-01-22,存档于 Wayback Machine。单值基础计划,先进研究院。
- Taylor, Melissa August, Harriet Barovick, Michelle Derrow, Tam Gray, Daniel S. Levy, Lina Lofaro, David Spitz, Joel Stein 和 Chris (1999 年 6 月 14 日),"本世纪最糟糕的 100 个想法",*时代杂志*,检索于 2025 年 4 月 12 日
- Frank Ruda (2011 年 10 月 6 日),*黑格尔的暴民:对黑格尔法哲学的研究*,Bloomsbury 出版,151 页,ISBN 978-1-4411-7413-0
- Adams, Stephen (1993 年 10 月),"功能珍珠 高效集合——平衡行为",*函数编程杂志*,第 3 卷,第 4 期:553–561,doi:10.1017/S0956796800000885,ISSN 1469-7653,检索于 2025 年 4 月 12 日
- Abbott, Stephen (2015),*理解分析*(第二版),纽约:Springer 出版社,第 3 页,ISBN 978-1-4939-2711-1
11. 参考文献
- Kunen, Kenneth (1980),*集合论:独立性证明导论*,North-Holland 出版社,ISBN 0-444-85401-0
- Johnson, Philip (1972),*集合论的历史*,Prindle, Weber & Schmidt 出版社,ISBN 0-87150-154-6
- Devlin, Keith (1993),*集合的乐趣:当代集合论基础*,数学本科教材系列(第二版),Springer Verlag,doi:10.1007/978-1-4612-0903-4,ISBN 0-387-94094-4
- Ferreirós, Jose (2001),*思想的迷宫:集合论及其在现代数学中的作用的历史*,柏林:Springer 出版社,ISBN 978-3-7643-5749-8
- Monk, J. Donald (1969),*集合论导论*,McGraw-Hill Book Company 出版社,ISBN 978-0-898-74006-6
- Potter, Michael (2004),*集合论及其哲学:批判性导论*,牛津大学出版社,ISBN 978-0-191-55643-2
- Smullyan, Raymond M.; Fitting, Melvin (2010),*集合论与连续统问题*,Dover Publications 出版社,ISBN 978-0-486-47484-7
- Tiles, Mary (2004),*集合论哲学:康托尔的乐园的历史性导论*,Dover Publications 出版社,ISBN 978-0-486-43520-6
- Dauben, Joseph W. (1977),"Georg Cantor 与教皇利奥十三世:数学、神学与无限",*思想史杂志*,第 38 卷,第 1 期:85–108,doi:10.2307/2708842,JSTOR 2708842
- Dauben, Joseph W. (1979),[不可在 archive.org 上获取] *Georg Cantor:他的数学与无限的哲学*,波士顿:哈佛大学出版社,ISBN 978-0-691-02447-9
12. 外部链接
- Daniel Cunningham,*集合论*文章,收录于*互联网哲学百科全书*
- Jose Ferreiros,"集合论的早期发展"文章,收录于*斯坦福哲学百科全书*
- Foreman, Matthew,Akihiro Kanamori,编。*集合论手册*。3 卷,2010 年。每一章节概述了当代集合论研究的某个方面。不涵盖已建立的基础集合论,关于此内容请参见 Devlin (1993)。
- "公理化集合论",*数学百科全书*,EMS 出版社,2001 年[1994]
- "集合论",*数学百科全书*,EMS 出版社,2001 年[1994]
- Schoenflies, Arthur (1898)。*克莱因百科全书中的集合论*
- 关于集合论的在线书籍和图书馆资源,您所在图书馆和其他图书馆提供的资源
- Rudin, Walter B. (1990 年 4 月 6 日),"集合论:分析的后代",马登数学讲座,威斯康星大学密尔沃基分校,原文存档于 2021 年 10 月 31 日 – 通过 YouTube
友情链接: 超理论坛 | ©小时科技 保留一切权利