中山大学 2011 年913专业基础（数据结构）考研真题

                     

贡献者： xzllxls

　　 声明：“该内容来源于网络公开资料，不保证真实性，如有侵权请联系管理员”

1. 一、单项选择题(每题 2 分，共 40 分)

　　 1.算法复杂度通常是表达算法在最坏情况下所需要的计算量，$O(1)$ 的含义是( )
(A).算法执行 1 步就完成
(B).算法执行 1 秒钟就完成
(C).解决执行常数步就完成
(D).算法执行可变步数就完成

　　 2.在数据结构中，按逻辑结构可把数据结构分为( )
(A).静态结构和动态结构
(B).线性结构和非线性结构
(C).顺序结构和链式结构
(D).内部结构和外部结构

　　 3.在数据结构中，可用存储顺序代表逻辑顺序的数据结构为( )
(A). Hash 表
(B).二叉搜索树
(C).链式结构
(D).顺序结构

　　 4. 对链式存储的正确描述是( )
(A).结点之间是连续存储的
(B).各结点的地址由小到大
(C).各结点类型可以不一致
(D).结点内单元是连续存储的

　　 5. 在下列关于 “串” 的陈述中，正确的说明是( )
(A).串是一种特殊的线性表
(B).串中元素只能是字母
(C).串的长度必须大于零
(D).空串就是空白串

　　 6.关于堆栈的正确描述是( )
(A). FILO
(B). FIFO
(C).只能用数组来实现
(D).可以修改栈中元素的数据

　　 7. 假设循环队列的长度为 QSize. 当队列非空时，从其队列头取出数据后，其队头下标 Front 的变化为()
(A). Front = Front+ 1
(B). Front = (Front + 1) % 100
(C). Front = (Front+ 1) % QSize
(D). Front = Front % Qsize + 1

　　 8. 假设 Head 是带头结点单向循环链的头结点指针，判断其为空的条件是( )
(A). Head.next = NULL
(B). Head~>next == Head
(C). Head->next = NULL
(D). Head = NULL

　　 9.设 A[)][m]为一个对称矩阵，数组下标从[0[0)开始。为了节省存储，将其下三角部分按行存放在一维数组 B0.m-1], m=n(n+1)2, 对下三角部分中任一元素 4.fi≥D, 它在一-维数组 B 的下标 k 值是( )
(A). i(i-1)/2+j
(B). (-1)2+j-1
(C). (i+1)/2+j-1
(D). i(+1)2+j

　　 10. 假设二又树的根结点为第 $0$ 层，那么，其第 $i$ 层($i\geqslant0$)的结点数最多为( )
(A).$2i$
(B).$2^i$
(C).$2^{i+1}-1$
(D).$2^{i+1}$

　　 11. 若一棵二叉树的后序和中序序列分别是 dbefca 和 dbaef,则其先序序列是( )
(A). adbefc
(B). abdcfe
(C). adbcef
(D). abdcef

　　 12.用一维数组来存储满二叉树，若数组下标从 0 开始，则元素下标为 k 的右子结点下标是( )(不考虑数组下标的越界问题)
(A). $2k+1$
(B). $2k+2$
(C). $ \lfloor k/2 \rfloor $
(D). $ \lceil k/2 \rceil $

　　 13. 假设 LTree 和 RTree 是二叉搜索树 Tree 的左右子树，H(T)表示树 T 的高度。若树 Tree 是 AVL 树，则( )
(A). H(LTree) - H(RTree)= 0
(B). HCLTree)- H(RTree) < 1
(C). H(LTree) - H(RTree) <= 1
(D). H(LTree) - H(RTree) <= 1

　　 14. 对 $n$ 个结点和 $e$ 条边的无向图(无环),其邻接矩阵中零元素的个数为( )
(A). $e$
(B). $2e$
(C). $n^2-e$
(D). $n^2-2e$

　　 15. 用邻接矩阵存储有 n 个顶点和 e 条边的有向图，则删除与某个顶点相邻的所有边的时间复杂度是()
(A). $O(n)$
(B). $O(e)$
(C). $O(n+e)$
(D). $O(ne)$

　　 16. 下列排序算法中，时间复杂度最差的是( )
(A).选择排序
(B).桶(基数)排序
(C).快速排序
(D).堆排序

　　 17. 基于比较的排序算法对 n 个数进行排序的比较次数下界为( )
(A). $O(logn)$
(B). $O(m)$
(C). $O(nlogn)$
(D). $O(n^2)$

　　 18. 在下列存储条件下，( )是最适合 使用折半查找算法来进行查找操作。
(A).顺序存储
(B).链式存储
(C).散列存储
(D).数据有序且顺序存储

　　 19. 在下列算法中，求图最小生成树的算法是( )
(A). DFS 算法
(B). KMP 算法
(C). Prim 算法
(D). Djkstra 算法

　　 20. 若结点的存储地址与其关键字之间存在某种映射关系，则称这种存储结构为( )
(A).顺序存储结构 $\qquad$ (B). 链式存储结构
(C).散列存储结构 $\qquad$ (D). 索引存储结构

2. 二、解答题(每题 10 分，共 50 分)

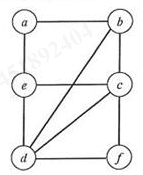
　　 1.假设有如图 1 所示的图
(1)写出图 1 的邻接矩阵;
(2)根据邻接矩阵从顶点 a 出发进行宽度(或广度)优先遍历，画出相应的宽度优先遍历树(同一个结点的邻接结点按结点序号大小为序)。

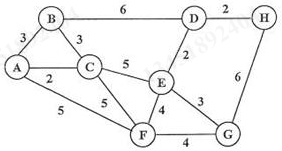
　　 2.简单描述求图最小生成树的 Kruskal 算法(克鲁斯卡尔算法)的基本思想，并按步骤列出图 2 的最小生成树的求解过程。

　　 3.简单叙述快速排序的思想，在 “第一个元素为支点” 前提下按步骤列出下列序列的排序过程。
待排序的数值序列: 45,12,56,87,34,78

　　 4. 已知有下列 13 个元素的散列表:

　　 其散列函数为 h(key)=key%m (m=13),处理冲突的方法为双重散列法，探查序列为:
$h=(h(key)+i*(key)\%m$ $\qquad$ $i=0.1.... m-1$, 其中:$h'(key)=key\%11+1$
间:对表中关键字 35 进行查找时，所需进行的比较次数为多少？依次写出每次的计算公式和值。s.假设设在通信中，字符 a, b,c,d, e,,g 出现的频率如下:
a:20% b: 7% $\quad$ c:16% $\quad$ d: 27% e: 7% $\quad$ f: 10% $\quad$ g: 13(1)根据 Huffman 算法(赫夫曼算法)画出其赫夫曼树:
(2)给出每个字母所对应的赫夫曼编码，规定:结点左分支边上标 0，右分支边上标 I;
(3)计算其加权路径的长度 WPL.

3. 三、阅读理解题，按空白编号填写相应的 C 语言语句，以实现函数功能。(每空 2 分，每题 10 分，共 30 分)

　　 1.排队是日常生活中常见的一种现象，比如:在商店排队付款。当第一位顾客完成付款离开后，其他顾客依次前移。下面用数据结构中的队列来模拟这种排队现象。

#define QUEUE 40
struct Queue {
    int queue[QUEUE];
    int Rear;
    int Rear;    // Rear 记录队列尾
};

(1)初始化队列 Q

void InitQueue(Queue *Q)
{
    Q->Rear=-1;
}

　　 (2)入队操作 EnQueu(Q, dat):若队列 Q 已满，返回 0，否则，把数据 data 加入队列 Q,并返回 1

int EnQueue(Queue *Q, int *data)
{
    if(__(1)__) return 0;
    __(2)__;
    Q->queue[Rear] = data;
    return 1;
}

　　 (3)出队操作 DeQueue(Q, dat):若队列 Q 为空，则返回 0,否则，把队头元素存入地址参数 data,然后从队列 Q 中去除该队头元素，并返回 1.

int DeQueue(Queue *Q, int *data)
{
    if(Q->Rear = -1) return 0;
    *data=___ (3)___;
    for(i=0; i<Q->Rear; i++) __ (4)__;
    __(5)__;
    return 1;
}

　　 2.假设有两个堆栈共享一个存储空间，其有关定义如下:

#define SIZE 50
struct Stacks {
    int Elements[SIZE];
    int Topl, Top2;    //Top1和Top2分别记录二个栈的栈顶
};

这二个堆栈在某个时刻的状态如下图所示。

　　 (1)初始化堆栈

void InitStacks(Stacks *stack)
{
    stack->Topl = ____ (1)___;
    stack->Top2 = ____ (2)___;
}

(2)堆栈 1(左堆栈)压栈操作

int pushl(Stacks *stack, int data)
{
    if( _ (3)_ ) return 0;
    stack->Top1++;
    Elements[stack->Top1]=data;
    return 1;
}

(3)堆栈 2(右堆栈)出栈操作，并把栈顶元素的值赋给指针变量 data 所指向的存储单元

BOOL pop2(Stacks *stack, int *data)
{
    if(___(4)___) return 0;
    *data = Elements[stack->Top2];
    ___(5)___;
    return 1;
}

　　 3.假设二叉树 $T=< T_L,root,T_R>$ 的深度定义如下:
$Depth(T)= \left\{\begin{aligned} &0, & T\text{是空树} \\ &1, & T\text{的根结点是叶结点} \\ & max(Depth(TL), Depth(TR)) & \text{其他} \end{aligned}\right. $
已知二叉树的结点定义如下:

struct BNode {
    int Key;
    struct BNode *LChild, *RChild;
};

函数 Depth(root)是求以结点 root 为根的二叉树深度。

int Depth(BNode *root)
{
    int dl, d2;
    if(root==__(1)__) return 0;
    if(___(2)___) return 1;
    d1=____(3)____;
    d2=____(4)____;
    return(___(5)___?d1:d2);
}

4. 四、算法设计题(每题 15 分，共 30 分)

　　 用 C 语言或类 C 语言实现下面函数的功能。

　　 1.假设用链表表示集合，集合链表的结点定义如下:

struct Set {
    int element;
    struct Set next
};

例如: A={2.1,3}，B=, 集合 A 和 B 的存储形式如下图所示。

　　 试实现集合的下列二个操作: (1) Set Intersection(Set *A, Set *B)，其功能是返回集合 A 和 B 交集的首结点地址(10 分)
(2) int Cardinality(Set *A),其功能是返回集合 A 中的元素个数，即:求|AI (5 分)
例如有下列语句:

Set *A, *B, *C;
int NumC;
......    //集合A和B的值由其它集合操作获得
C = Intersection(A, B);    //C=A交B
NumC = Cardinality(C);     // NumC=|C|

　　 2.已知二叉树的结点定义如下:

struct BNode {
    int Key;
    struct BNode *LChild, *RChild;
};

编写函数 TraveralByLeve(BNode *ro0), 其功能是 “按层” 遍历以结点 roo 为根的二叉树，并输出每个结点中 Key 的信息。
在函数描述中可直接使用下列队列功能(如果需要的话，仅供参考)

Queue:队列类型定义符
InitQueue(Queue *Q):初始化队列Q为空队列
EnQueue(Queue *Q, BNode *node);:把指针node入队列Q
BNode *DeQueue(Queue *Q):若队列Q为空，则返回NULL,否则，返回队头元素，并从队列Q中删除该队头元索
int QueueEmpty(Queue *Q):若队列Q为空，则返回1,否则，返回0