深度优先搜索算法

贡献者：待更新

　　（本文根据 CC-BY-SA 协议转载自原搜狗科学百科对英文维基百科的翻译）

　　 深度优先搜索（DFS)是用于遍历或搜索树或图数据结构的算法。该算法从根节点开始(在图的情况下选择一些任意节点作为根节点)，并在回溯之前尽可能沿着每个分支进行探索。

　　法国数学家查尔斯·皮埃尔·特雷毛[1]为解决迷宫的策略,在 19 世纪研究了深度优先搜索。[2][3]

1. 属性

　　 DFS 的时间和空间分析因其应用领域而异。在理论计算机科学中，DFS 通常用于遍历整个图，并且需要时间为 $O(|V| + |E|)$,[4]且图的大小是线性的。在这些应用中，它也使用空间 $O(|V|)$，最坏的情况是存储当前搜索路径上的顶点堆栈以及一组已经访问过的顶点。因此，在此设置中，时间和空间界限与广度优先搜索相同，选择使用这两种算法中的哪一种较少取决于它们的复杂度，而更多地取决于这两种算法产生的顶点排序的不同属性。

　　适用于与特定领域相关的 DFS 应用，例如在人工智能中搜索解决方案或者网络爬虫，要遍历的图通常要么太大而不能完整访问，要么是无限的(DFS 可能会遭受不终止)。在这种情况下，搜索仅在有限深度的情况下进行；由于资源有限，例如内存或磁盘空间，通常不使用数据结构来跟踪所有先前访问过的顶点的集合。当在有限的深度中搜索时，时间在扩展顶点和边的数量方面仍然是线性的(尽管由于一些顶点可能被搜索不止一次，而其他顶点根本不被搜索，导致这个数量与整个图的大小不同)，但是 DFS 的这种变体的空间复杂度仅与深度限制成比例，因此远小于使用广度优先搜索搜索到相同深度所需的空间。对于这样的应用，DFS 也更适合选择看起来很可能的分支的启发式方法。当事先不知道合适的深度极限时，迭代深化深度优先搜索以递增的限制顺序重复应用 DFS。在人工智能的分析模式下，一个分子因子如果深度大于 1，迭代加深会使运行时间增加一个常数因子，在这种情况下，由于每层节点数的几何增长，正确的深度限制是已知的。

　　 DFS 也可以用于收集图节点的样本。然而，与不完全的 BFS 相似，不完全的 DFS 对高度的节点有偏差。

2. 例子

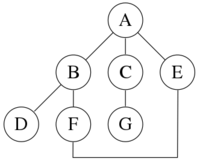
　　对于下图:

图 1

　　深度优先搜索从 A 开始，假设图中的左边缘在右边缘之前已经被选择，并且假设搜索记住以前访问过的节点，并且不会重复搜索(因为这是一个小图)，将按以下顺序访问节点: $A,B,D,F,E,C,g$。在这样的边缘遍历搜索下建立 Trémaux 树，这是一种图论中有重要应用的结构。执行相同的搜索而不记住先前访问的节点会导致访问节点的顺序为 $A,B,D,F,E,A,B,D,F,E,$ 等。永远陷入 $A,B,D,F,E,$ 循环，且永远不会达到 $C$ 或 $G$。

　　迭代深化是避免这种无限循环的一种技术，并将到达所有节点。

3. 深度优先搜索的输出

图 2：由生成树定义的四种类型的边

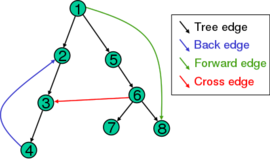
　　图的深度优先搜索的一种方便的描述是用搜索过程中到达的顶点的生成树来表示的。基于这个生成树，原始图的边可以分为三类:前边缘，它从树的一个节点指向它的一个后代节点，后边缘，它从一个节点指向它先前的节点之一，交叉边缘，不使用前边缘和后边缘。有时树边缘属于生成树本身，树边缘的边与前向边分开分类。如果原始图是无向图，那么它的所有边都是树边缘或后边缘。

3.1 DFS 排序

　　如果一个图的顶点的枚举是 DFS 应用于该图的可能的输出，则称之为 DFS 排序。$G = (V, E)$ 形成带有 $n$ 个顶点的图。$\sigma = (v_1, \ldots, v_m)$ 是 $V$ 的不同元素的列表，对于 $v \in V \setminus \\{v_1, \ldots, v_m}$，让 $\nu_\sigma(v)$ 成为最大的 $i$，如果这样一个 $i$ 存在，则 $v_i$ 是 $v$ 的邻邻，否则为 $0$。

　　让 $\sigma = (v_1, \ldots, v_n)$ 是 $V$ 的顶点的枚举。如果对所有 $1 \leq i \leq n$，$v_i$ 是顶点 $v \in V \setminus {v_1, \ldots, v_{i-1}}$，则枚举 $\sigma$ 是 DFS 排序(有源 $v_1$)，且 $(v_1, \ldots, v_{i-1})$ 是 $v_i$ 的一组近邻。同样地，如果对所有 $v_i \in N(v_k) \setminus N(v_j)$ 的 $1 \leq j < k \leq n$ 来说，存在有一个 $v_j$ 的近邻 $v_m$ 使得 $i < m < j$，则 $\sigma$ 是 DFS 的一种排序。

3.2 顶点排序

　　也可以使用深度优先搜索对图或树的顶点进行线性排序。有三种常见的方法:

先置排序是顶点的列表，该列表按照深度优先搜索算法访问顶点的顺序进行排列。如前文所述，这是描述搜索过程的一种简洁自然的方式。表达式树的先置排序是波兰表示法中的表达式。
后置排序是顶点的列表，该列表按照后被算法访问顺序进行排列。表达式树的后序是逆波兰表示法中表达式的反向。
反向后置与后置排序相反，即顶点的列表与它们上次访问的顺序相反。反向后置与先置排序不同。

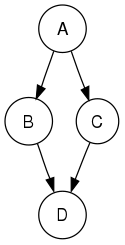
　　例如，当从节点 A 开始搜索下面的有向图时，遍历的序列要么是 $A B D B A C A$，要么是 $A C D C A B A$ (选择从 $A$ 第一次访问 $B$ 还是 $C$ 取决于算法)。请注意，这里包括以回溯到节点的形式重复访问，以检查它是否仍然有未访问的近邻(即使没有发现的情况下)。因此，可能的先置排序是 $A B D C$ 和 $A C D B$，而可能的后置排序是 $D B C A$ 和 $D C B A$，可能的反向后置排序是 $A C B D$ 和 $A B C D$。

　　反向后置排序产生任何一个有向无环图的一个拓扑排序。这种排序在控制流分析方面也很有用，因为它通常表示控制流的自然线性化。上图可能表示下面代码片段中的控制流，按 $A B C D$ 或 $A C B D$ 的顺序考虑该代码是自然的，但使用 $A B D C$ 或 $A C D B$ 的顺序是不自然的。

图 3

if (A) then {
  B
} else {
  C
}
D

4. 伪代码

　　输入:图 G 和 G 的顶点 v

　　输出:v 中被标记的可被发现的所有顶点

　　 DFS 的递归实现：[5]

1  procedure DFS(G,v):
2      label v as discovered
3      for all directed edges from v to w that are in G.adjacentEdges(v) do
4          if vertex w is not labeled as discovered then
5              recursively call DFS(G,w)

通过该算法发现顶点的顺序被称为字典顺序。

　　最坏空间复杂度下离散傅里叶变换的非递归实现 $O(|E|) \\ (d)$:[6]

1  procedure DFS-iterative(G,v):
2      let S be a stack
3      S.push(v)
4      while S is not empty
5          v = S.pop()
6          if v is not labeled as discovered:
7              label v as discovered
8              for all edges from v to w in G.adjacentEdges(v) do 
9                  S.push(w)

DFS 的这两个变体以彼此相反的顺序访问每个顶点的相邻顶点: 递归变体访问的 v 的第一个相邻顶点是相邻边列表中的第一个，而在迭代变体中，第一个访问的近邻是相邻边列表中的最后一个。递归实现将按以下顺序访问示例图中的节点: $A,B,D,F,E,C,G$。非递归实现将访问以下节点：$A,E,F,B,D,C,G$。

　　非递归实现类似于广度优先搜索，但有两个不同之处:

它使用堆栈而不是队列
它会延迟检查顶点是否已被发现，直到该顶点从堆栈中弹出，而不是在添加顶点之前进行此检查。

5. 应用

　　使用深度优先搜索作为构建块的算法包括:

图 4：用于生成迷宫的类似于深度优先搜索的随机化算法。

查找连接的组件。
拓扑排序。
查找 2-(边或顶点)-连接的组件。
查找 3-(边或顶点)-连接的组件。
寻找图的桥。
生成单词以绘制组的极限集。
寻找强连接分量。
平面度测试。[7][8]
仅用一个解决方案解决难题，例如迷宫(DFS 可以通过仅包括在访问集中当前路径上的节点，应用于找到迷宫的所有解决方案。)
迷宫生成可以使用随机深度优先搜索。
在图中寻找双连接性。

6. 复杂性

　　约翰·赖夫研究了 DFS 的计算复杂性。更准确地说，给定一个图表 $G$，让 $O= (v_1, \ldots, v_n)$ 由标准递归 DFS 算法计算的顺序。这种排序被称为词典深度优先搜索排序。约翰·赖夫考虑了给定图和源的情况下，计算词典深度优先搜索顺序的复杂性。问题的决策版本(测试在此排序下，某个顶点 $u$ 是否发生在某个顶点 $v$ 之前)是P-complete,[9]这意味着这是 “并行处理的噩梦”。[10]

　　深度优先搜索顺序(不一定是字典顺序)，可以通过复杂度类 RNC 中的随机并行算法来计算。[11]截至 1997 年，深度优先遍历是否可以由复杂度类为 NC 的确定性并行算法构建仍然是未知的。[12]

7. 笔记

查尔斯·皮埃尔·特雷毛(1859-1882)巴黎的巴黎综合理工学院(X:1876)，法国电报工程师在 2010 年 12 月 2 日的公开会议上——由教授主讲让·佩尔蒂埃-塞伯特在梅肯学院(勃艮第-法国)–(摘要发表在年报学术版，2011 年 3 月)–ISSN 0980-6032)
Even, Shimon (2011), Graph Algorithms (2nd ed.), Cambridge University Press, pp. 46–48, ISBN 978-0-521-73653-4。
Sedgewick, Robert (2002), Algorithms in C++: Graph Algorithms (3rd ed.), Pearson Education, ISBN 978-0-201-36118-6。
科曼、托马斯·h、查尔斯·e·莱塞森和罗纳德·L·李维斯特。p.606
古德里奇和塔马西亚；科曼、莱瑟森、瑞文斯特和斯坦
第 93 页，算法设计，克莱因伯格和塔多斯
Hopcroft, John; Tarjan, Robert E. (1974), "Efficient planarity testing", Journal of the Association for Computing Machinery, 21 (4): 549–568, doi:10.1145/321850.321852。
de Fraysseix, H.; Ossona de Mendez, P.; Rosenstiehl, P. (2006), "Trémaux Trees and Planarity", International Journal of Foundations of Computer Science, 17 (5): 1017–1030, arXiv:math/0610935, doi:10.1142/S0129054106004248。
Reif, John H. (1985). "Depth-first search is inherently sequential". Information Processing Letters. 20 (5). doi:10.1016/0020-0190(85)90024-9.
Mehlhorn, Kurt; Sanders, Peter (2008). Algorithms and Data Structures: The Basic Toolbox (PDF). Springer.
Aggarwal, A.; Anderson, R. J. (1988), "A random NC algorithm for depth first search", Combinatorica, 8 (1): 1–12, doi:10.1007/BF02122548, MR 0951989。
Karger, David R.; Motwani, Rajeev (1997), "An NC algorithm for minimum cuts", SIAM Journal on Computing, 26 (1): 255–272, CiteSeerX 10.1.1.33.1701, doi:10.1137/S0097539794273083, MR 1431256。

8. 参考文献

　　 [1] ^查尔斯·皮埃尔·特雷毛(1859-1882)巴黎的巴黎综合理工学院(X:1876)，法国电报工程师在 2010 年 12 月 2 日的公开会议上——由教授主讲让·佩尔蒂埃-塞伯特在梅肯学院(勃艮第-法国)–(摘要发表在年报学术版，2011 年 3 月)–ISSN 0980-6032).

　　 [2] ^Even, Shimon (2011), Graph Algorithms (2nd ed.), Cambridge University Press, pp. 46–48, ISBN 978-0-521-73653-4。.

　　 [3] ^Sedgewick, Robert (2002), Algorithms in C++: Graph Algorithms (3rd ed.), Pearson Education, ISBN 978-0-201-36118-6。.

　　 [4] ^科曼、托马斯·h、查尔斯·e·莱塞森和罗纳德·L·李维斯特。p.606.

　　 [5] ^古德里奇和塔马西亚；科曼、莱瑟森、瑞文斯特和斯坦.

　　 [6] ^第 93 页，算法设计，克莱因伯格和塔多斯.

　　 [7] ^Hopcroft, John; Tarjan, Robert E. (1974), "Efficient planarity testing", Journal of the Association for Computing Machinery, 21 (4): 549–568, doi:10.1145/321850.321852。.

　　 [8] ^de Fraysseix, H.; Ossona de Mendez, P.; Rosenstiehl, P. (2006), "Trémaux Trees and Planarity", International Journal of Foundations of Computer Science, 17 (5): 1017–1030, arXiv:math/0610935, doi:10.1142/S0129054106004248。.

　　 [9] ^Reif, John H. (1985). "Depth-first search is inherently sequential". Information Processing Letters. 20 (5). doi:10.1016/0020-0190(85)90024-9..

　　 [10] ^Mehlhorn, Kurt; Sanders, Peter (2008). Algorithms and Data Structures: The Basic Toolbox (PDF). Springer..

　　 [11] ^Aggarwal, A.; Anderson, R. J. (1988), "A random NC algorithm for depth first search", Combinatorica, 8 (1): 1–12, doi:10.1007/BF02122548, MR 0951989。.

　　 [12] ^Karger, David R.; Motwani, Rajeev (1997), "An NC algorithm for minimum cuts", SIAM Journal on Computing, 26 (1): 255–272, CiteSeerX 10.1.1.33.1701, doi:10.1137/S0097539794273083, MR 1431256。.

致读者：小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。因此，我们请求广大读者热心打赏 ，使网站得以健康发展。如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损，并在接下来的一年里向所有读者继续免费提供优质内容。但遗憾的是只有不到 1% 的读者愿意捐款，他们的付出帮助了 99% 的读者免费获取知识，我们在此表示感谢。