普朗克常数（综述）

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 普朗克常数，记作 \( h \)，是量子力学中一个具有基础性重要性的物理常数：一个光子的能量等于其频率与普朗克常数的乘积，物质波的波长等于普朗克常数除以相关粒子的动量。与之密切相关的约化普朗克常数，等于 \( \frac{h}{2\pi} \)，通常用 \( \hbar \) 表示，在量子物理方程中广泛使用。

　　 这个常数由马克斯·普朗克在 1900 年提出，作为解释实验黑体辐射所需的比例常数。\(^\text{[2]}\) 普朗克后来将这个常数称为 “作用量子”。\(^\text{[3]}\)1905 年，阿尔伯特·爱因斯坦将 “量子” 或能量的最小元素与电磁波本身联系起来。马克斯·普朗克因其 “通过发现能量量子对物理学发展的贡献” 而获得了 1918 年诺贝尔物理学奖。

　　 在计量学中，普朗克常数与其他常数一起，用来定义千克，即质量的国际单位制（SI）单位。\(^\text{[4]}\) 国际单位制的定义方式使得当普朗克常数以国际单位制单位表示时，其精确值为 \( h = 6.62607015 \times 10^{-34} \, \text{J} \cdot \text{Hz}^{-1} \)。\(^\text{[5][6]}\)

1. 历史

常数的起源

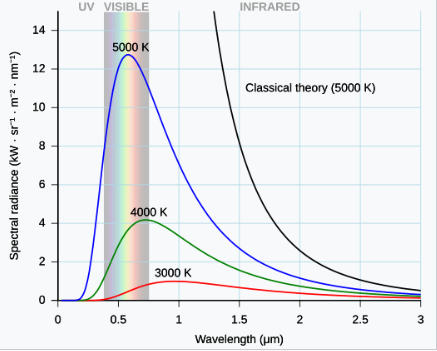
　　 普朗克常数是作为马克斯·普朗克成功努力的一部分提出的，普朗克试图推导出一个数学表达式，准确预测从封闭炉子（黑体辐射）中观察到的热辐射谱分布。\(^\text{[7]}\) 这个数学表达式现在被称为普朗克定律。

　　 在 19 世纪的最后几年，马克斯·普朗克正在研究黑体辐射的问题，这个问题大约 40 年前由基尔霍夫首次提出。每个物体都会自发地、持续地发射电磁辐射。然而，观察到的辐射光谱的整体形状并没有表达式或解释。当时，维恩定律能够很好地拟合短波长和高温的数据，但对于长波长则失败了。\(^\text{[7]: 141}\) 同时，尽管普朗克尚不知情，雷利勋爵已经理论推导出了一个公式，现在称为雷利-简定律，该公式能够合理地预测长波长，但在短波长处表现得非常不准确。

　　 普朗克试图找到一个数学表达式，既能重现维恩定律（适用于短波长），又能重现经验公式（适用于长波长）。这个表达式包括一个常数 \(h\)，这个常数被认为是 Hilfsgröße（辅助量），\(^\text{[8]}\) 并随后成为了普朗克常数。普朗克所提出的表达式表明，某物体在绝对温度 \(T\) 下，对于频率 \(\nu\) 的频率单位辐射光谱辐照度为： \[ B_{\nu}(\nu, T) d\nu = \frac{2h\nu^3}{c^2} \frac{1}{e^{\frac{h\nu}{k_{\mathrm{B}}T}} - 1} d\nu,~ \] 其中 \(k_{\text{B}}\) 是玻尔兹曼常数，\(h\) 是普朗克常数，\(c\) 是介质中的光速，无论是物质还是真空。\(^\text{[9][10][11]}\)

　　 普朗克很快意识到他的解并不是唯一的。存在几种不同的解，每种解给出的振荡器熵值都不同。\(^\text{[2]}\) 为了挽救他的理论，普朗克采用了当时颇具争议的统计力学理论，\(^\text{[2]}\) 他将其描述为 “一种绝望的尝试”。他的一个新边界条件是：

　　 将 \( U_N \)[‘N 个振荡器的振动能量’] 解释为不是一个连续的、可以无限分割的量，而是作为一个由有限数量相等部分组成的离散量。我们称每一部分为能量元素 \(\varepsilon\)；

　　 ——普朗克，《关于正常谱中能量分布的定律》\(^\text{[2]}\)

　　 通过这一新条件，普朗克对振荡器的能量进行了量子化，正如他自己所说，“这只是一个纯粹的形式假设……实际上我并没有多想”，\(^\text{[13]}\) 但这个假设却将彻底改变物理学。将这一新方法应用于维恩位移定律，表明 “能量元素” 必须与振荡器的频率成正比，这就是现在有时被称为 “普朗克-爱因斯坦关系” 的第一个版本： \[ E = hf.~ \] 普朗克能够通过黑体辐射的实验数据计算出普朗克常数 \(h\) 的值：他的结果为 \( 6.55 \times 10^{-34} \, \text{J} \cdot \text{s}\)，与当前定义的值相差仅 1.2%。\(^\text{[2]}\) 他还通过相同的数据和理论首次确定了玻尔兹曼常数 \(k_{\text{B}}\) 的值。\(^\text{[14]}\)

发展与应用

　　 黑体问题在 1905 年再次被讨论，当时雷利勋爵和詹姆斯·简斯（共同）以及阿尔伯特·爱因斯坦独立证明了经典电磁学永远无法解释观察到的光谱。这些证明通常被称为 “紫外灾难”，这个名称是保罗·爱伦费斯特在 1911 年提出的。它们（连同爱因斯坦关于光电效应的工作）极大地促使物理学家相信，普朗克关于量子化能级的假设不仅仅是一个数学形式主义。1911 年第一次索尔维会议专门讨论了 “辐射和量子理论”。\(^\text{[15]}\)

光电效应

　　 光电效应是指当光照射到表面时，表面释放出电子（称为 “光电子”）。它首次由亚历山大·埃德蒙·贝克雷尔于 1839 年观察到，尽管通常将荣誉归于海因里希·赫兹，\(^\text{[16]}\) 他于 1887 年发表了第一次全面的研究。另一个特别详细的研究由菲利普·莱纳德于 1902 年发表。\(^\text{[17]}\) 爱因斯坦 1905 年关于光量子的论文 \(^\text{[18]}\) 讨论了这一效应，这使得他在 1921 年获得了诺贝尔奖，\(^\text{[16]}\) 这一奖项是在罗伯特·安德鲁·米利肯的实验工作验证了爱因斯坦的预测之后颁发的。诺贝尔委员会将奖项颁给他在光电效应方面的工作，而非相对论，部分原因是存在偏见，认为纯理论物理学如果没有基于发现或实验的支持，就不值得授奖，同时委员会成员对相对论是否真实的证明存在分歧。\(^\text{[20][21]}\)

　　 在爱因斯坦的论文之前，电磁辐射，如可见光，被认为表现为波的性质：因此，使用 “频率” 和 “波长” 来描述不同类型的辐射。波在给定时间内传递的能量称为其强度。剧院聚光灯的光比家庭灯泡的光更强烈；也就是说，聚光灯在单位时间和单位空间内释放的能量比普通灯泡多（因此消耗更多电力），即使光的颜色可能非常相似。其他波，如声音或冲击海岸线的海浪，也有其强度。然而，光电效应的能量解释似乎与光的波动描述不一致。

　　 由于光电效应产生的 “光电子” 具有一定的动能，这些动能可以被测量。每个光电子的动能与光的强度无关，\(^\text{[17]}\) 但与频率呈线性关系；\(^\text{[19]}\) 如果频率过低（对应的光子能量小于材料的功函数），则根本不会发射任何光电子，除非多个光子，其能量之和大于光电子的能量，几乎同时作用（多光子效应）。\(^\text{[22][23]}\) 假设频率足够高以引发光电效应，光源强度的增加会导致更多的光电子以相同的动能被发射出来，而不是以更高的动能发射相同数量的光电子。\(^\text{[17]}\)

　　 爱因斯坦对这些观察结果的解释是，光本身是量子化的；光的能量不是像经典波那样连续传递的，而是以小 “包” 或量子的形式传递。这些 “能量包” 的大小，后来被命名为光子，将与普朗克的 “能量元素” 相同，从而得出了普朗克-爱因斯坦关系的现代版本： \[ E = hf.~ \] 爱因斯坦的假设后来通过实验得到了验证：入射光的频率 \( f \) 与光电子的动能 \( E \) 之间的比例常数被证明等于普朗克常数 \( h \)。\(^\text{[19]}\)

原子结构

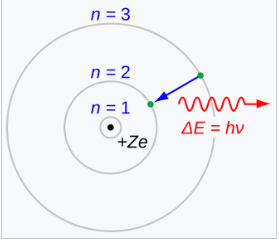
　　 在 1912 年，约翰·威廉·尼科尔森开发了 \(^\text{[24]}\) 一种原子模型，并发现模型中电子的角动量与 \(h/2\pi\) 相关。\(^\text{[25][26]}\) 尼科尔森的核量子原子模型影响了尼尔斯·波尔原子模型的发展，\(^\text{[27][28][26]}\) 波尔在他的 1913 年关于波尔模型的论文中引用了他。\(^\text{[29]}\) 波尔的模型超越了普朗克的抽象谐振子概念：波尔原子中的电子只能具有某些特定的能量 \( E_n \)，由以下公式定义： \[ E_n = -\frac{hcR_{\infty}}{n^2},~ \] 其中 \( c \) 是真空中的光速，\( R_{\infty} \) 是一个通过实验确定的常数（瑞德伯常数），\( n \in \{1, 2, 3, \dots\} \)。这种方法还使波尔能够解释瑞德伯公式，这是氢的原子光谱的经验描述，并能通过其他基本常数来解释瑞德伯常数 \(R_{\infty}\) 的值。在讨论模型中电子的角动量时，波尔引入了量 \(\frac{h}{2\pi} \)，现在被称为约化普朗克常数，作为角动量的量子。\(^\text{[29]}\)

不确定性原理

　　 普朗克常数也出现在维尔纳·海森堡不确定性原理的表述中。对于多个处于相同状态的粒子，它们的位置不确定性 \( \Delta x \) 和动量不确定性 \( \Delta p_x \) 满足如下关系： \[ \Delta x \, \Delta p_x \geq \frac{\hbar}{2},~ \] 其中，不确定性被定义为测量值与期望值之间的标准差。还有几个其他类似的物理可测共轭变量对，它们也遵循类似的规则。一个例子是时间与能量。两个共轭变量之间的不确定性反比关系在量子实验中强迫进行权衡，因为更精确地测量一个量会导致另一个量变得不精确。

　　 除了量子力学公式中某些值解释的假设外，整个理论的一个基本基石在于位置算符 \( \hat{x} \) 和动量算符 \( \hat{p} \) 之间的对易关系： \[ [{\hat {p}}_{i},{\hat {x}}_{j}] = -i\hbar \delta_{ij},~ \] 其中 \( \delta_{ij} \) 是克罗内克δ符号。

光子能量

　　 普朗克关系将特定的光子能量 \( E \) 与其相关的波频率 \( f \) 连接起来： \[ E = hf.~ \] 就普通感知的日常物体而言，这个能量极其微小。

　　 由于频率 \( f \)、波长 \( \lambda \) 和光速 \( c \) 之间的关系为 \( f = \frac{c}{\lambda} \)，该关系也可以表示为： \[ E = \frac{hc}{\lambda}.~ \]

德布罗意波长

　　 1923 年，路易·德布罗意通过假设普朗克常数代表不仅是光子的动量与量子波长之间的比例关系，而且是任何粒子的量子波长与动量之间的比例关系，推广了普朗克-爱因斯坦关系。此假设很快通过实验得到了验证。这一关系适用于整个量子理论，包括电动力学。粒子的德布罗意波长 \(\lambda\) 由以下公式给出： \[ \lambda = \frac{h}{p},~ \] 其中 \( p \) 表示粒子的线动量，例如光子或任何其他基本粒子。

　　 具有角频率 \( \omega = 2\pi f \) 的光子的能量由以下公式给出： \[ E = \hbar \omega,~ \] 而其线动量与以下关系相关： \[ p = \hbar k,~ \] 其中 \( k \) 是角波数。

　　 这两个关系是使用四维向量的特殊相对论表达式的时间和空间部分。 \[ P^{\mu} = \left( \frac{E}{c}, \vec{p} \right) = \hbar K^{\mu} = \hbar \left( \frac{\omega}{c}, \vec{k} \right).~ \]

统计力学

　　 经典统计力学要求存在普朗克常数 \(h\)（但不定义其值）。\(^\text{[30]}\) 最终，继普朗克的发现之后，物理学家猜测，物理作用不能取任意值，而是被限制为一个非常小的量——"[基本的]作用量子"——的整数倍，这个量现在被称为普朗克常数。\(^\text{[31]}\) 这是所谓的 “旧量子理论” 的一个重要概念部分，该理论由包括波尔、索末菲和石原在内的物理学家发展而来，在这一理论中，粒子轨迹存在但被隐藏，量子规律根据它们的作用约束这些轨迹。这一观点已被完全现代的量子理论所取代，在现代量子理论中，甚至没有确定的运动轨迹；相反，粒子由一个在空间和时间中展开的波函数表示。\(^\text{[32]: 373 }\) 与此相关的是能量量子化的概念，这在旧量子理论中存在，并且以变体形式在现代量子物理中也存在。经典物理学无法解释能量的量子化。

2. 维度和数值

　　 维度和数值 普朗克常数具有与作用和角动量相同的维度。普朗克常数的值被固定为 \( h = 6.62607015 \times 10^{-34} \, \text{J} \cdot \text{Hz}^{-1} \)\(^\text{[5] }\)，作为国际单位制（SI）单位定义的一部分。\(^\text{[33] }\) 另一种情况是，如果弧度被视为基本单位，则 \( h \) 将具有作用量的维度，而 \( \hbar \) 将具有角动量的维度。\(^\text{[34] }\)

　　 这个数值用于定义国际单位制中的质量单位——千克：“千克[…] 是通过将普朗克常数 \(h\) 的固定数值设定为 \( h = 6.62607015 \times 10^{-34}\)（当以 J⋅s 单位表示时，等于 \( \text{kg} \cdot \text{m}^2 \cdot \text{s}^{-1}\)）来定义的，其中米和秒是通过光速 \(c\) 和未经扰动的铯-133 原子基态超精细跃迁的持续时间 \(\Delta \nu_{\text{Cs}}\) 来定义的。”\(^\text{[35] }\) 质量计量学技术，如基于普朗克常数固定值的基布尔平衡仪，用于精确测量千克的数值。

数值的意义

　　 普朗克常数是物理学中最小的常数之一。这反映了这样一个事实：在人类适应的尺度上，能量通常是千焦耳量级，时间通常是秒或分钟量级，普朗克常数非常小。当一个物理事件的能量与时间的乘积接近普朗克常数时，量子效应主导了该事件的行为。\(^\text{[36] }\)

　　 同样地，普朗克常数的数量级反映了日常物体和系统由大量微观粒子构成这一事实。例如，在绿色光（波长为 555 纳米或频率为 540 THz）中，每个光子的能量为 \( E = hf = 3.58 \times 10^{-19} \, \text{J} \)。就日常经验而言，这是一非常小的能量，但日常经验并不关心单个光子，就像不关心单个原子或分子一样。日常经验中更典型的光量（虽然远大于人眼可感知的最小量）是 1 摩尔光子的能量；其能量可以通过将光子能量乘以阿伏伽德罗常数 \( N_A = 6.02214076 \times 10^{23} \, \text{mol}^{-1} \)\(^\text{[37] }\) 来计算，结果为 216 kJ，大约等于一个小新鲜苹果中的食物能量。\(^\text{[38] }\)

3. 约化普朗克常数

　　 量子物理中的许多方程通常使用约化普朗克常数 \( \hbar \)，其等于 \( \frac{h}{2\pi} \)，并表示为 \( \hbar \)（发音为 h-bar）。\(^\text{[39]: 104 [40]: 336 [41] }\)

　　 使用 \( \hbar \) 编写基本方程比使用 \( h \) 更简单，通常在进行量级估算时，使用 \( \hbar \) 而非 \( h \) 能得到更可靠的结果。例如，使用维度分析估算氢原子的电离能时，确定电离能 \( E_i \) 的相关参数是电子的质量 \( m_e \)、电子电荷 \( e \)，以及普朗克常数 \( h \) 或约化普朗克常数 \( \hbar \)： \[ E_i \propto m_e \frac{e^4}{h^2} \quad \text{或} \quad \propto m_e \frac{e^4}{\hbar^2}~ \] 由于这两个常数具有相同的维度，它们将在维度分析中以相同的方式出现，但使用 \( \hbar \) 时估算误差在两倍以内，而使用 \( h \) 时误差接近 \( (2\pi)^2 \approx 40 \)。\(^\text{[42]: 8–9 }\)

名称和符号

　　 约化普朗克常数有许多其他名称：约化普朗克常数 \(^\text{[43]: 5 [44]: 788 )}\)，规范化普朗克常数 \(^\text{[45]: 726 [46]: 10 [47]}\):-（或规范化普朗克常数 \(^\text{[48]: 334 [49]: ix [50]: 112 }\)），狄拉克常数 \(^\text{[51]: 275 [45]: 726 [52]: xv}\)（或狄拉克的常数 \(^\text{[[53]: 148 [54]: 604 [55]: 313] }\)），狄拉克 \(h\)\(^\text{[56][57]: xviii }\)（或狄拉克的 \(h\)\(^\text{[58]: 17 }\)），狄拉克 \(\hbar\)\(^\text{[59]: 187 }\)（或狄拉克的 \( \hbar\)\(^\text{[60]: 273 [61]: 14 }\)），以及 h-bar。\(^\text{[62]: 558 [63]: 561 }\)。通常也会将这个 \(\hbar\) 称为 “普朗克常数”\(^\text{[64]: 55  [a] }\)，同时保持关系 \(\hbar = \frac{h}{2\pi} \)。

　　 目前最常见的约化普朗克常数符号是 \( \hbar \)。然而，也有一些来源使用 \( h \) 来表示它，在这种情况下，它们通常称其为 “狄拉克 \( h \)”\(^\text{[90]: 43 [91] }\)（或 “狄拉克的 \( h \)”\(^\text{[92]: 21 }\) ）。

历史

　　 组合 \(\frac{h}{2\pi}\) 首次出现在尼尔斯·波尔 1913 年的论文中，\(^\text{[93]: 15 }\) 其中它被表示为 \(M_0\)\(^\text{[26]: 169 [b] }\) 。在接下来的 15 年里，这个组合继续出现在文献中，但通常没有单独的符号 \(^\text{[94]: 180 [c] }\) 然后，在 1926 年，施罗丁格和狄拉克在他们的开创性论文中再次引入了特殊的符号：施罗丁格使用 \(K\)\(^\text{[106] }\)，狄拉克使用 \( h \)\(^\text{[107] }\)。狄拉克继续以这种方式使用 \(h\)，直到 1930 年，\(^\text{[108]: 291 }\) 当时他在他的《量子力学原理》一书中引入了符号 \(\hbar\)\(^\text{[108]: 291 [109] }\)。

4. 参见

• 国际科学理事会数据委员会
• 国际单位制
• 量子力学简介
• 以科学家名字命名的物理常数列表
• 普朗克单位
• 波粒二象性

5. 注释

　　
a.此类用法的显著例子包括兰道和利夫希茨[65]: 20 以及格里菲思[66]: 3 ，当然还有许多其他例子。[67][68]: 449 [69]: 284 [70]: 3 [71]: 365 [72]: 14 [73]: 18 [74]: 4 [75]: 138 [76]: 251 [77]: 1 [78]: 622 [79]: xx [80]: 20 [81]: 4 [82]: 36 [83]: 41 [84]: 199 [85]: 846 [86][87][88]: 25 [89]: 653 [过多引用]
b.波尔用 \( M \) 表示电子围绕原子核的角动量，并将量子化条件写为 \( M = \tau M_0 \)，其中 \( \tau \) 是正整数。（参见波尔模型。）
c.以下是一些在[94]中提到的论文，其中 \( \frac{h}{2\pi} \) 出现但没有单独符号：[95]: 428  [96]: 549  [97]: 508  [98]: 230  [99]: 458  [100][101]: 276  [102][103][104].[105]

6. 参考文献

引文

1. "Planck constant". The NIST Reference on Constants, Units, and Uncertainty. NIST. 2019 年 5 月 20 日. 原文存档于 2022 年 5 月 27 日。于 2023 年 9 月 3 日检索。
2. Planck, Max (1901), "Ueber das Gesetz der Energieverteilung im Normalspectrum" (PDF), Annalen der Physik (德文), 309 (3): 553–63, Bibcode:1901AnP...309..553P, doi:10.1002/andp.19013090310, 原文存档（PDF）于 2012 年 6 月 10 日，2008 年 12 月 15 日检索。英文翻译： "On the Law of Distribution of Energy in the Normal Spectrum". 原文存档于 2008 年 4 月 18 日。 "On the Law of Distribution of Energy in the Normal Spectrum" (PDF). 原文存档（PDF）于 2011 年 10 月 6 日。2011 年 10 月 13 日检索。
3. "Max Planck Nobel Lecture". 原文存档于 2023 年 7 月 14 日。2023 年 7 月 14 日检索。
4. 《国际单位制》（PDF）（第 9 版），国际度量衡局，2022 年 12 月，第 131 页，ISBN 978-92-822-2272-0
5. "2022 CODATA Value: Planck constant". The NIST Reference on Constants, Units, and Uncertainty. NIST. 2024 年 5 月。于 2024 年 5 月 18 日检索。
6. "Resolutions of the 26th CGPM" (PDF). BIPM. 2018 年 11 月 16 日。原文存档（PDF）于 2018 年 11 月 19 日。2018 年 11 月 20 日检索。
7. Bitter, Francis; Medicus, Heinrich A. (1973). Fields and particles. New York: Elsevier. 第 137–144 页。
8. Boya, Luis J. (2004). "The Thermal Radiation Formula of Planck (1900)". arXiv:physics/0402064v1.
9. Planck, M. (1914). The Theory of Heat Radiation. 由 Masius, M. 翻译（第 2 版）。P. Blakiston's Son. 第 6、168 页。OL 7154661M。
10. Chandrasekhar, S. (1960) [1950]. Radiative Transfer (修订版再版)。Dover. 第 8 页。ISBN 978-0-486-60590-6。
11. Rybicki, G. B.; Lightman, A. P. (1979). Radiative Processes in Astrophysics. Wiley. 第 22 页. ISBN 978-0-471-82759-7. 原文存档于 2020 年 7 月 27 日。于 2020 年 5 月 20 日检索。
12. Kragh, Helge (2000 年 12 月 1 日), Max Planck: the reluctant revolutionary, PhysicsWorld.com, 原文存档于 2009 年 1 月 8 日
13. Kragh, Helge (1999), Quantum Generations: A History of
14. Physics in the Twentieth Century, Princeton University Press, 第 62 页, ISBN 978-0-691-09552-3, 原文存档于 2021 年 12 月 6 日，2021 年 10 月 31 日检索
15. Planck, Max (1920 年 6 月 2 日), The Genesis and Present State of Development of the Quantum Theory (诺贝尔讲座), 原文存档于 2011 年 7 月 15 日，2008 年 12 月 13 日检索
16. Previous Solvay Conferences on Physics, International Solvay Institutes, 原文存档于 2008 年 12 月 16 日，2008 年 12 月 12 日检索 参见，例如，Arrhenius, Svante (1922 年 12 月 10 日). "Presentation speech of the 1921 Nobel Prize for Physics". 原文存档于 2011 年 9 月 4 日。2008 年 12 月 13 日检索。
17. Lenard, P. (1902). "Ueber die lichtelektrische Wirkung". Annalen der Physik. 313 (5): 149–198. Bibcode:1902AnP...313..149L. doi:10.1002/andp.19023130510. 原文存档于 2019 年 8 月 18 日。2019 年 7 月 3 日检索。
18. Einstein, Albert (1905). "Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt" (PDF). Annalen der Physik. 17 (6): 132–48. Bibcode:1905AnP...322..132E. doi:10.1002/andp.19053220607. 原文存档（PDF）于 2011 年 7 月 9 日。2009 年 12 月 3 日检索。
19. Millikan, R. A. (1916). "A Direct Photoelectric Determination of Planck's h". Physical Review. 7 (3): 355–88. Bibcode:1916PhRv....7..355M. doi:10.1103/PhysRev.7.355.
20. Isaacson, Walter (2007 年 4 月 10 日). Einstein: His Life and Universe. Simon and Schuster. 第 309–314 页. ISBN 978-1-4165-3932-2. 原文存档于 2020 年 1 月 9 日。2021 年 10 月 31 日检索。
21. "The Nobel Prize in Physics 1921". Nobel Foundation. 原文存档于 2018 年 7 月 3 日。2014 年 4 月 23 日检索。
22. Smith, Richard (1962). "Two Photon Photoelectric Effect". Physical Review. 128 (5): 2225. Bibcode:1962PhRv..128.2225S. doi:10.1103/PhysRev.128.2225.
23. Smith, Richard (1963). "Two-Photon Photoelectric Effect". Physical Review. 130 (6): 2599. Bibcode:1963PhRv..130.2599S. doi:10.1103/PhysRev.130.2599.4.
24. Nicholson, J. W. (1912). "The Constitution of the Solar Corona II". Monthly Notices of the Royal Astronomical Society. 72 (8): 677–693. doi:10.1093/mnras/72.8.677.
25. Heilbron, John L. (2013). "The path to the quantum atom". Nature. 498 (7452): 27–30. doi:10.1038/498027a. PMID 23739408. S2CID 4355108.
26. McCormmach, Russell (1966). "The Atomic Theory of John William Nicholson". Archive for History of Exact Sciences. 3 (2): 160–184. doi:10.1007/BF00357268. JSTOR 41133258. S2CID 120797894.
27. Hirosige, Tetu; Nisio, Sigeko (1964). "Formation of Bohr's theory of atomic constitution". Japanese Studies in History of Science. 3: 6–28.
28. Heilbron, J. L. (1964). A History of Atomic Models from the Discovery of the Electron to the Beginnings of Quantum Mechanics (博士论文). 加利福尼亚大学伯克利分校。
29. Bohr, Neils (1913). "On the constitution of atoms and molecules". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 第六系列. 26 (151): 1–25. Bibcode:1913PMag...26..476B. doi:10.1080/14786441308634955. 原文存档于 2023 年 3 月 7 日。2023 年 7 月 23 日检索。
30. Giuseppe Morandi; F. Napoli; E. Ercolessi (2001), Statistical mechanics: an intermediate course, World Scientific, 第 84 页, ISBN 978-981-02-4477-4, 原文存档于 2021 年 12 月 6 日，2021 年 10 月 31 日检索
31. ter Haar, D. (1967). The Old Quantum Theory. Pergamon Press. 第 133 页. ISBN 978-0-08-012101-7.
32. Einstein, Albert (2003). "Physics and Reality" (PDF). Daedalus. 132 (4): 24. doi:10.1162/001152603771338742. S2CID 57559543. 原文存档（PDF）于 2012 年 4 月 15 日。问题首先是：如何给一个在经典力学意义上指定的系统分配一系列离散的能量值 \( H_{\sigma} \)（能量函数是坐标 \( q_r \) 和相应动量 \( p_r \) 的给定函数）？普朗克常数 \( h \) 将频率 \( H_{\sigma}/h \) 与能量值 \( H_{\sigma} \) 关联起来。因此，只需给系统一系列离散的频率值即可。
33. 《国际单位制》（PDF）（第 9 版），国际度量衡局，2022 年 12 月，ISBN 978-92-822-2272-0
34. Quincey, Paul; Brown, Richard J C (2016 年 6 月 1 日). "Implications of adopting plane angle as a base quantity in the SI". Metrologia. 53 (3): 998–1002. arXiv:1604.02373. doi:10.1088/0026-1394/53/3/998. ISSN 0026-1394. 2025 年 2 月 22 日检索。
35. 《国际单位制》（PDF）（第 9 版），国际度量衡局，2022 年 12 月，ISBN 978-92-822-2272-0
36. "The Feynman Lectures on Physics Vol. II Ch. 19: The Principle of Least Action". www.feynmanlectures.caltech.edu. 2023 年 11 月 3 日检索。
37. "2022 CODATA Value: Avogadro constant". The NIST Reference on Constants, Units, and Uncertainty. NIST. 2024 年 5 月。2024 年 5 月 18 日检索。
38. Angelo, Joseph (2020). Energy of Matter (修订版). Infobase Publishing. 第 17 页. ISBN 9781438195803. 一颗小新鲜苹果含有约 53 卡路里（220 千焦）；
39. Schwarz, Patricia M.; Schwarz, John H. (2004 年 3 月 25 日). Special Relativity: From Einstein to Strings. Cambridge University Press. ISBN 978-1-139-44950-2.
40. Chabay, Ruth W.; Sherwood, Bruce A. (2017 年 11 月 20 日). Matter and Interactions. John Wiley & Sons. ISBN 978-1-119-45575-2.
41. "reduced Planck constant". The NIST Reference on Constants, Units, and Uncertainty. NIST. 2019 年 5 月 20 日. 原文存档于 2023 年 4 月 8 日。2023 年 9 月 3 日检索。
42. Lévy-Leblond, Jean-Marc (2002). "The meanings of Planck's constant" (PDF). In Beltrametti, E.; Rimini, A.; Robotti, Nadia (eds.). One Hundred Years of H: Pavia, 2000 年 9 月 14-16 日. 意大利物理学会. ISBN 978-88-7438-003-9. 原文存档（PDF）于 2023 年 10 月 14 日。
43. Huang, Kerson (2010 年 4 月 26 日). Quantum Field Theory: From Operators to Path Integrals. John Wiley & Sons. ISBN 978-3-527-40846-7.
44. Schmitz, Kenneth S. (2016 年 11 月 11 日). Physical Chemistry: Concepts and Theory. Elsevier. ISBN 978-0-12-800600-9.
45. Rennie, Richard; Law, Jonathan, eds. (2017). "Planck constant". A Dictionary of Physics. Oxford Quick Reference（第 7 版）。英国牛津：牛津大学出版社。ISBN 978-0198821472.
46. The International Encyclopedia of Physical Chemistry and Chemical Physics. Pergamon Press. 1960.
47. Vértes, Attila; Nagy, Sándor; Klencsár, Zoltán; Lovas, Rezso György; Rösch, Frank (2010 年 12 月 10 日). Handbook of Nuclear Chemistry. Springer Science & Business Media. ISBN 978-1-4419-0719-6.
48. Bethe, Hans A.; Salpeter, Edwin E. (1957). "Quantum Mechanics of One- and Two-Electron Atoms". In Flügge, Siegfried (ed.). Handbuch der Physik: Atome I–II. Springer.
49. Lang, Kenneth (2013 年 11 月 11 日). Astrophysical Formulae: A Compendium for the Physicist and Astrophysicist. Springer Science & Business Media. ISBN 978-3-662-11188-8.
50. Galgani, L.; Carati, A.; Pozzi, B. (2002 年 12 月). "The Problem of the Rate of Thermalization, and the Relations between Classical and Quantum Mechanics". In Fabrizio, Mauro; Morro, Angelo (eds.). Mathematical Models and Methods for Smart Materials, Cortona, Italy, 2001 年 6 月 25 日至 29 日. 第 111–122 页. doi:10.1142/9789812776273_0011. ISBN 978-981-238-235-1.
51. 福克斯，马克（2018 年 6 月 14 日）。《原子物理学学生指南》。剑桥大学出版社。ISBN 978-1-316-99309-5。
52. 克莱斯，罗纳德（2021 年 6 月 10 日）。《量子场论：图解法》。剑桥大学出版社。ISBN 978-1-108-78750-5。
53. 佐胡里，巴赫曼（2021 年 1 月 5 日）。《高功率激光能量对材料的热效应》。施普林格自然出版集团。ISBN 978-3-030-63064-5。
54. 巴利安，罗杰（2007 年 6 月 26 日）。《从微物理学到宏物理学：统计物理学的方法与应用》。第二卷。施普林格科学与商业媒体。ISBN 978-3-540-45480-9。
55. 陈，C. 朱利安（2011 年 8 月 15 日）。《太阳能物理学》。约翰·威利与子公司出版。ISBN 978-1-118-04459-9。
56. "Dirac h"。大英百科全书。原文存档于 2023 年 2 月 17 日。检索于 2023 年 9 月 27 日。
57. 肖恩伯格，D.（2009 年 9 月 3 日）。《金属中的磁振荡》。剑桥大学出版社。ISBN 978-1-316-58317-3。
58. 鲍威尔，约翰·L.；克拉塞曼，伯恩德（2015 年 5 月 5 日）。《量子力学》。库里尔·多佛出版公司。ISBN 978-0-486-80478-1。
59. 德雷斯登，马克斯（2012 年 12 月 6 日）。《H.A. 克拉梅尔：传统与革命之间》。施普林格科学与商业媒体。ISBN 978-1-4612-4622-0。
60. 约翰逊，R. E.（2012 年 12 月 6 日）。《原子与分子碰撞导论》。施普林格科学与商业媒体。ISBN 978-1-4684-8448-9。
61. 加西亚，亚历杭德罗；亨利，厄内斯特·M.（2007 年 7 月 13 日）。《亚核物理学》（第 3 版）。世界科技出版公司。ISBN 978-981-310-167-8。
62. 霍尔布罗，查尔斯·H.；劳埃德，詹姆斯·N.；阿马托，约瑟夫·C.；加尔维斯，恩里克；帕克斯，M. 伊丽莎白（2010 年 9 月 14 日）。《现代基础物理学》。纽约：施普林格科学与商业媒体。ISBN 978-0-387-79080-0。
63. 波利亚宁，安德烈·D.；切尔努察，阿列克谢（2010 年 10 月 18 日）。《数学、物理学与工程科学简明手册》。CRC 出版社。ISBN 978-1-4398-0640-1。
64. 道林，乔纳森·P.（2020 年 8 月 24 日）。《薛定谔的网络：构建量子互联网的竞赛》。CRC 出版社。ISBN 978-1-000-08017-9。
65. 兰道，L. D.；利夫希茨，E. M.（2013 年 10 月 22 日）。《量子力学：非相对论理论》。爱思唯尔出版社。ISBN 978-1-4831-4912-7。
66. 格里菲斯，大卫·J.；施罗特，达雷尔·F.（2019 年 11 月 20 日）。《量子力学导论》。剑桥大学出版社。ISBN 978-1-108-10314-5。
67. “普朗克常数”。《大苏联百科全书》（第 3 版）。盖尔集团。1970-1979 年。
68. 伊齐克森，克劳德；祖贝尔，让-伯纳德（2012 年 9 月 20 日）。《量子场论》。库里尔公司。ISBN 978-0-486-13469-7。
69. 加库，Michio（1993 年）。《量子场论：现代导论》。牛津大学出版社。ISBN 978-0-19-507652-3。
70. 博戈柳博夫，尼古拉·尼古拉耶维奇；谢尔科夫，德米特里·瓦西里耶维奇（1982 年）。《量子场》。本杰明/卡明斯出版公司，进阶图书计划/世界科学部门。ISBN 978-0-8053-0983-6。
71. 艾奇森，伊恩·J·R.；海伊，安东尼·J·G.（2012 年 12 月 17 日）。《粒子物理中的规范理论：实践导论：从相对论量子力学到量子电动力学》（第 4 版）。CRC 出版社。ISBN 978-1-4665-1299-3。
72. 德·维特，B.；史密斯，J.（2012 年 12 月 2 日）。《粒子物理中的场论》。第 1 卷。爱思唯尔出版社。ISBN 978-0-444-59622-2。
73. 布朗，洛威尔·S.（1992 年）。《量子场论》。剑桥大学出版社。ISBN 978-0-521-46946-3。
74. 布赫宾德，伊奥西夫·L.；沙皮罗，伊利亚（2021 年 3 月）。《量子场论导论与量子引力的应用》。牛津大学出版社。ISBN 978-0-19-883831-9。
75. 贾菲，阿瑟（2004 年 3 月 25 日）。“9. 量子场论在大局中如何定位？” 收录于曹天宇（编）。《量子场论的概念基础》。剑桥大学出版社。ISBN 978-0-521-60272-3。
76. 卡比博，尼古拉；马伊阿尼，卢西亚诺；本哈尔，奥马尔（2017 年 7 月 28 日）。《规范理论导论》。CRC 出版社。ISBN 978-1-4987-3452-3。
77. 卡萨尔布奥尼，罗伯托（2017 年 4 月 6 日）。《量子场论导论》（第 2 版）。世界科技出版公司。ISBN 978-981-314-668-6。
78. 达斯，阿肖克（2020 年 7 月 24 日）。《量子场论讲座》（第 2 版）。世界科技出版公司。ISBN 978-981-12-2088-3。
79. 德赛，比平·R.（2010 年）。《量子力学与基础场论》。剑桥大学出版社。ISBN 978-0-521-87760-2。
80. 多诺休，约翰；索尔博，洛伦佐（2022 年 3 月 8 日）。《量子场论前奏》。普林斯顿大学出版社。ISBN 978-0-691-22348-3。
81. 福兰德，杰拉尔德·B.（2021 年 2 月 3 日）。《量子场论：数学家的旅游指南》。美国数学学会。ISBN 978-1-4704-6483-7。
82. 弗拉德金，爱德华多（2021 年 3 月 23 日）。《量子场论：一种综合方法》。普林斯顿大学出版社。ISBN 978-0-691-14908-0。
83. 热利斯，弗朗索瓦（2019 年 7 月 11 日）。《量子场论》。剑桥大学出版社。ISBN 978-1-108-48090-1。
84. 格雷纳，沃尔特；赖因哈特，乔阿希姆（2013 年 3 月 9 日）。《量子电动力学》。施普林格科学与商业媒体。ISBN 978-3-662-05246-4。
85. 利博夫，理查德·L.（2003 年）。《量子力学导论》（第 4 版）。旧金山：皮尔逊教育公司。ISBN 978-81-317-0441-7。
86. 巴鲁特，A. O.（1978 年 8 月 1 日）。“光子的产生：普朗克常数ħ或精细结构常数α的启发式计算”。《自然科学期刊 A》。33（8）：993–994。Bibcode:1978ZNatA..33..993B。doi:10.1515/zna-1978-0819。S2CID 45829793。
87. 科西亚，卢卡斯；洛夫，彼得（2018 年 7 月 12 日）。“测量背景性与普朗克常数”。《新物理学杂志》。20（7）：073020。arXiv:1711.08066。Bibcode:2018NJPh...20g3020K。doi:10.1088/1367-2630/aacef2。S2CID 73623448。
88. 汉弗里斯，戴维（2022 年 11 月 28 日）。“普朗克常数的隐含结构”。《欧洲应用物理学杂志》。4（6）：22–25。doi:10.24018/ejphysics.2022.4.6.227。S2CID 254359279。
89. 贝斯，F. 亚历山大；法默，J. 多伊恩（2008 年）。“信息物理学”。收录于阿德里安斯，彼得；范本特姆，约翰（编）。《信息哲学》。科学哲学手册。第 8 卷。阿姆斯特丹：北荷兰出版社。arXiv:0708.2837。ISBN 978-0-444-51726-5。
90. 广田，E.；坂木马，H.；猪俣，K.（2013 年 3 月 9 日）。《巨磁电阻器件》。施普林格科学与商业媒体。ISBN 978-3-662-04777-4。
91. 加德纳，约翰·H.（1988 年）。“不变性理论”。《百科全书》。65：139。
92. 莱文，拉斐尔·D.（2009 年 6 月 4 日）。《分子反应动力学》。剑桥大学出版社。ISBN 978-1-139-44287-9。
93. 玻尔，N.（1913 年 7 月）。“I. 原子和分子的构成”。《伦敦、爱丁堡和都柏林哲学杂志与科学杂志》。26（151）：1–25。Bibcode:1913PMag...26....1B。doi:10.1080/14786441308634955。
94. 梅赫拉，贾吉什；雷亨贝格，赫尔穆特（1982 年 8 月 3 日）。《量子理论的历史发展》。第 1 卷。施普林格纽约出版社。ISBN 978-0-387-90642-3。
95. 索末菲，A.（1915 年）。“关于巴尔默系列的理论”（PDF）。《慕尼黑皇家学会数学物理学部会议报告》。33（198）：425–458。doi:10.1140/epjh/e2013-40053-8。
96. 施瓦茨希尔德，K.（1916 年）。“关于量子假说”。《柏林普鲁士皇家科学院会议报告》：548–568。
97. 埃伦费斯特，P.（1917 年 6 月）。“XLVIII. 绝热不变量与量子理论”。《伦敦、爱丁堡和都柏林哲学杂志与科学杂志》。33（198）：500–513。doi:10.1080/14786440608635664。
98. 兰德，A.（1919 年 6 月）。“氦的系列光谱”。《物理学杂志》。20：228–234。
99. 玻尔，N.（1920 年 10 月）。“关于元素系列光谱”。《物理学杂志》。2（5）：423–469。Bibcode:1920ZPhy....2..423B。doi:10.1007/BF01329978。
100. 斯特恩，奥托（1921 年 12 月）。“在磁场中实验性验证方向量子化的一种方法”。《物理学杂志》。7（1）：249–253。Bibcode:1921ZPhy....7..249S。doi:10.1007/BF01332793。
101. 海森堡，维尔纳（1922 年 12 月）。“关于线结构和异常塞曼效应的量子理论”。《物理学杂志》。8（1）：273–297。Bibcode:1922ZPhy....8..273H。doi:10.1007/BF01329602。
102. 克拉梅尔斯，H. A.；保利，W.（1923 年 12 月）。“关于带光谱的理论”。《物理学杂志》。13（1）：351–367。Bibcode:1923ZPhy...13..351K。doi:10.1007/BF01328226。
103. 博恩，M.；约旦，P.（1925 年 12 月）。“关于量子力学”。《物理学杂志》。34（1）：858–888。Bibcode:1925ZPhy...34..858B。doi:10.1007/BF01328531。
104. 狄拉克，P. A. M.（1925 年 12 月）。“量子力学的基本方程”。《伦敦皇家学会会刊 A 辑，含数学与物理学论文》。109（752）：642–653。Bibcode:1925RSPSA.109..642D。doi:10.1098/rspa.1925.0150。
105. 博恩，M.；海森堡，W.；约旦，P.（1926 年 8 月）。“关于量子力学。II”。《物理学杂志》。35（8-9）：557–615。Bibcode:1926ZPhy...35..557B。doi:10.1007/BF01379806。
106. 薛定谔，厄尔温（1926 年）。“量子化作为本征值问题”。《物理年鉴》。384（4）：361–376。Bibcode:1926AnP...384..361S。doi:10.1002/andp.19263840404。
107. 狄拉克，保罗·A·M.（1926 年 10 月）。“关于量子力学的理论”。《伦敦皇家学会会刊 A 辑，含数学与物理学论文》。112（762）：661–677。Bibcode:1926RSPSA.112..661D。doi:10.1098/rspa.1926.0133。
108. 梅赫拉，贾吉什；雷亨贝格，赫尔穆特（2000 年）。《量子理论的历史发展》。第 6 卷。纽约：施普林格出版社。
109. 狄拉克，保罗·A·M.（1930 年）。《量子力学原理》（第 1 版）。英国牛津：克拉伦登出版社。

来源

• 巴罗，约翰·D.（2002 年）。《自然常数：从阿尔法到欧米伽——编码宇宙最深奥秘密的数字》。潘 thon 图书出版公司。ISBN 978-0-375-42221-8。

7. 外部链接

• “普朗克常数在物理学中的作用” – 2018 年 11 月在法国凡尔赛举行的第 26 届 CGPM 会议上的报告。
• “普朗克常数及其单位” – 2019 年 11 月 3 日在加拿大安大略省滑铁卢市滑铁卢大学举行的第 35 届化学物理学研讨会上的报告。