密度矩阵（综述）

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 在量子力学中，密度矩阵（或密度算符）是描述物理系统集体（即使该集体仅包含一个系统）作为量子态的矩阵。它允许通过博恩规则计算对集体中各系统进行测量后的结果概率。密度矩阵是比常见的状态向量或波函数更一般的概念：状态向量或波函数只能表示纯态，而密度矩阵也能表示混合集体（有时模糊地称为混合态）。混合集体在量子力学中有两种情况：

1. 当系统的准备导致集体中有多个纯态时，需要处理可能准备的统计分布；
2. 当想要描述一个与另一个系统纠缠的物理系统时，而不描述它们的组合态；这种情况通常出现在系统与某些环境交互时（例如去相干）。在这种情况下，纠缠系统的密度矩阵不同于由多个纯态组成的集体的密度矩阵，后者在测量时会给出相同的统计结果。

　　 因此，密度矩阵在处理混合集体的量子力学领域中是至关重要的工具，如量子统计力学、开放量子系统和量子信息等。

1. 定义与动机

　　 密度矩阵是一个线性算符的表示，称为密度算符。密度矩阵是通过在基础空间中选择一个正交规范基来从密度算符中得到的。[2]实际上，密度矩阵和密度算符这两个术语常常可以互换使用。

　　 假设选择一个基，其中有两个状态 \(|0\rangle\) 和 \(|1\rangle\) 在二维希尔伯特空间中，那么密度算符可以表示为矩阵： \[ (\rho_{ij}) = \left( \begin{matrix} \rho_{00} & \rho_{01} \\ \rho_{10} & \rho_{11} \end{matrix} \right) = \left( \begin{matrix} p_0 & \rho_{01} \\ \rho_{01}^* & p_1 \end{matrix} \right)~ \] 其中对角元素是实数，并且它们的和为 1（也称为两个状态 \(|0\rangle\) 和 \(|1\rangle\) 的占据数）。非对角元素是彼此的复共轭（也称为相干性）；它们的幅度受到密度算符是正半定算符这一要求的限制，见下文。

　　 密度算符是一个正半定的自伴算符，其迹为 1，并作用于系统的希尔伯特空间。[3][4][5]这一定义可以通过考虑一个情况来动机化，其中每个纯态 \(|\psi_j\rangle\) 以概率 \(p_j\) 被准备，描述的是一个纯态的集体。在使用投影算符 \(\Pi_m\) 时，获得投影测量结果 \(m\) 的概率由以下公式给出[6]： \[ p(m) = \sum_j p_j \langle \psi_j | \Pi_m | \psi_j \rangle = \operatorname{tr} \left[\Pi_m \left( \sum_j p_j |\psi_j \rangle \langle \psi_j | \right) \right]~ \] 这使得密度算符定义为： \[ \rho = \sum_j p_j |\psi_j \rangle \langle \psi_j |~ \] 成为这个集体状态的一个方便表示。可以很容易地验证，这个算符是正半定的，自伴的，并且具有迹为 1。反过来，根据谱定理，任何具有这些性质的算符都可以写成：\(\sum_j p_j |\psi_j \rangle \langle \psi_j |\) 其中 \( |\psi_j \rangle \) 是某些状态，且系数 \(p_j\) 非负且其和为 1。[7][6]然而，如施罗德–HJW 定理所示，这个表示并不唯一。

　　 密度算符定义的另一个动机来自于考虑对纠缠态的局部测量。设 \(|\Psi\rangle\) 是复合希尔伯特空间 \(\mathcal{H}_1 \otimes \mathcal{H}_2\) 中的一个纯纠缠态。当在希尔伯特空间 \(\mathcal{H}_1\) 上对投影算符 \(\Pi_m\) 进行测量时，获得测量结果 \(m\) 的概率由下式给出[6]： \[ p(m) = \langle \Psi | (\Pi_m \otimes I) | \Psi \rangle = \operatorname{tr} \left[ \Pi_m \left( \operatorname{tr}_2 |\Psi \rangle \langle \Psi | \right) \right]~ \] 其中，\(\operatorname{tr}_2\) 表示对希尔伯特空间 \(\mathcal{H}_2\) 的部分迹运算。这使得算符： \[ \rho = \operatorname{tr}_2 |\Psi \rangle \langle \Psi |~ \] 成为计算这些局部测量概率的一个方便工具。它被称为纯态 \(|\Psi\rangle\) 在子系统 1 上的约化密度矩阵。可以很容易地验证，这个算符具有所有密度算符的性质。反过来，施罗德–HJW 定理意味着，所有密度算符都可以写成：\(\operatorname{tr}_2 |\Psi \rangle \langle \Psi |\) 对于某个状态 \(|\Psi \rangle\)。

2. 纯态和混合态

　　 纯量子态是无法写成其他量子态的概率混合或凸组合的状态。[5]用密度算符的语言来说，纯态有几个等价的表述。[8]: 73 如果密度算符满足以下条件之一，则它表示一个纯态：

• 它可以写成一个状态向量 \(|\psi \rangle\) 与其自身的外积，即： \[ \rho = |\psi \rangle \langle \psi |~ \]
• 它是一个投影算符，特别是一个秩为一的投影。
• 它是幂等的，即： \[ \rho = \rho^2~ \]
• 它的纯度为 1，即： \[ \operatorname{tr}(\rho^2) = 1~ \]

　　 重要的是要强调量子态的概率混合（即集体）与两个态的叠加之间的区别。如果一个集体被准备为一半的系统处于态 \(|\psi_1\rangle\)，另一半处于态 \(|\psi_2\rangle\)，它可以通过密度矩阵描述： \[ \rho = \frac{1}{2} \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}~ \] 这里假设 \(|\psi_1\rangle\) 和 \(|\psi_2\rangle\) 是正交的，并且维度为 2，为了简化计算。另一方面，这两种态的量子叠加，且具有相等的概率振幅，结果是纯态：\(\psi\rangle = \frac{1}{\sqrt{2}} (|\psi_1\rangle + |\psi_2\rangle)\) 其对应的密度矩阵为： \[ |\psi \rangle \langle \psi | = \frac{1}{2} \begin{pmatrix} 1 & 1 \\ 1 & 1 \end{pmatrix}~ \] 与概率混合不同，这种叠加态能够展示量子干涉效应。[6]: 81

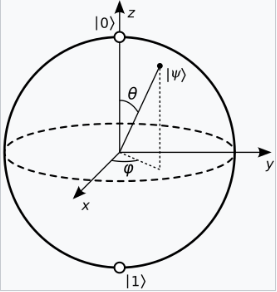
　　 从几何上讲，密度算符的集合是一个凸集合，纯态是该集合的极值点。最简单的情况是二维希尔伯特空间，即量子比特（qubit）。量子比特的任意混合态可以表示为保利矩阵的线性组合，保利矩阵与单位矩阵一起提供了 \(2 \times 2\) 自伴矩阵的基：[9]: 126  \[ \rho = \frac{1}{2} \left(I + r_x \sigma_x + r_y \sigma_y + r_z \sigma_z\right),~ \] 其中实数 \((r_x, r_y, r_z)\) 是单位球内某点的坐标，而 \[ \sigma_x = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}, \quad \sigma_y = \begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix}, \quad \sigma_z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}.~ \] 满足 \(r_x^2 + r_y^2 + r_z^2 = 1\) 的点表示纯态，而混合态则由单位球内部的点表示。这被称为量子比特态空间的布洛赫球模型（Bloch sphere picture）。

例子：光的偏振

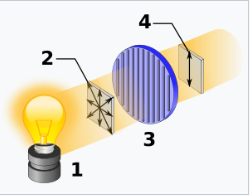
　　 纯态和混合态的一个例子是光的偏振。一个单个光子可以被描述为具有右旋或左旋圆偏振，分别由正交的量子态 \( |\mathrm{R} \rangle \) 和 \( |\mathrm{L} \rangle \) 表示，或者是这两者的叠加态：它可以处于任意态 \( \alpha |\mathrm{R} \rangle + \beta |\mathrm{L} \rangle \)（其中 \( |\alpha|^2 + |\beta|^2 = 1 \)），对应于线性、圆形或椭圆偏振。现在考虑一个垂直偏振的光子，由态 \( |\mathrm{V} \rangle = (|\mathrm{R} \rangle + |\mathrm{L} \rangle)/\sqrt{2} \) 描述。如果将其通过一个圆偏振片，该偏振片只能通过 \( |\mathrm{R} \rangle \) 偏振光，或者只能通过 \( |\mathrm{L} \rangle \) 偏振光，则两种情况下有一半的光子被吸收。这可能让人觉得一半的光子处于 \( |\mathrm{R} \rangle \) 态，另一半处于 \( |\mathrm{L} \rangle \) 态，但这并不正确：如果我们将 \( (|\mathrm{R} \rangle + |\mathrm{L} \rangle)/\sqrt{2} \) 通过线性偏振片，就没有任何光子被吸收；而如果我们将 \( |\mathrm{R} \rangle \) 或 \( |\mathrm{L} \rangle \) 通过偏振片，则有一半的光子会被吸收。

　　 非偏振光（例如白炽灯发出的光）不能被描述为任何形式的 \( \alpha |\mathrm{R} \rangle + \beta |\mathrm{L} \rangle \) 态（线性、圆形或椭圆偏振）。与偏振光不同，非偏振光通过偏振片时无论偏振片的方向如何，都会以 50%的强度损失通过；并且它不能通过任何波片被偏振。然而，非偏振光可以被描述为一个统计集，比如每个光子以 50%的概率具有 \( |\mathrm{R} \rangle \) 偏振或 \( |\mathrm{L} \rangle \) 偏振。如果每个光子具有垂直偏振 \( |\mathrm{V} \rangle \) 或水平偏振 \( |\mathrm{H} \rangle \) 也有 50%的概率，情况也是一样的。这两个集在实验上是完全不可区分的，因此它们被认为是相同的混合态。对于这个非偏振光的例子，密度算符为： \[ \rho = \frac{1}{2} |\mathrm{R} \rangle \langle \mathrm{R} | + \frac{1}{2} |\mathrm{L} \rangle \langle \mathrm{L} | = \frac{1}{2} |\mathrm{H} \rangle \langle \mathrm{H} | + \frac{1}{2} |\mathrm{V} \rangle \langle \mathrm{V} | = \frac{1}{2} \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}.~ \] 还有其他方法可以生成非偏振光：一种可能性是通过引入光子的制备不确定性，例如将光子通过一个双折射晶体，其表面粗糙，使得光束的不同部分获得不同的偏振。另一种可能性是使用纠缠态：一个放射性衰变可以发射两个朝相反方向传播的光子，量子态为 \( (|\mathrm{R}, \mathrm{L} \rangle + |\mathrm{L}, \mathrm{R} \rangle)/\sqrt{2} \)。这两个光子的联合态是纯态，但通过对联合密度矩阵进行部分迹运算得到的每个光子的密度矩阵是完全混合的。

3. 等效的集合和纯化

　　 给定的密度算符并不能唯一确定生成它的纯态集；一般来说，存在无限多种不同的集合作用生成相同的密度矩阵。这些集合作用无法通过任何测量来区分。等效集可以被完全表征：设 \(\{ p_j, |\psi_j\rangle \}\) 为一个集合。那么对于任何复矩阵 \(U\)，使得 \( U^\dagger U = I \)（部分酉算符），由以下定义的集合 \(\{ q_i, |\varphi_i\rangle \}\) 也会生成相同的密度算符，并且所有等效的集合作用都具有这种形式： \[ \sqrt{q_i} |\varphi_i\rangle = \sum_j U_{ij} \sqrt{p_j} |\psi_j\rangle~ \] 一个紧密相关的事实是，给定的密度算符有无数个不同的纯化态，纯化态是那些在进行部分迹运算时生成该密度算符的纯态。设 \[\rho = \sum_j p_j |\psi_j\rangle \langle \psi_j|~\] 为由集合 \(\{ p_j, |\psi_j\rangle \}\) 生成的密度算符，其中状态 \( |\psi_j\rangle \) 不一定是正交的。然后对于所有部分酉算符 \( U \)，我们有： \[ |\Psi\rangle = \sum_j \sqrt{p_j} |\psi_j\rangle U |a_j\rangle~ \] 这是一种纯化态，其中 \( |a_j\rangle \) 是正交基。此外，所有的纯化态都具有这种形式。

4. 测量

　　 设 \(A\) 为系统的可观察量，假设集合处于混合态，使得每个纯态 \( |\psi_j\rangle \) 以概率 \( p_j \) 发生。那么，对应的密度算符为 \[ \rho = \sum_j p_j |\psi_j\rangle \langle \psi_j|~ \] 可以通过从纯态的情况推广来计算测量的期望值： \[ \langle A \rangle = \sum_j p_j \langle \psi_j | A | \psi_j \rangle = \sum_j p_j \operatorname{tr} \left( |\psi_j\rangle \langle \psi_j| A \right) = \operatorname{tr} \left( \sum_j p_j |\psi_j\rangle \langle \psi_j| A \right) = \operatorname{tr} (\rho A)~ \] 其中，\(\operatorname{tr}\) 表示迹运算。因此，熟悉的纯态期望值表达式 \(\langle A \rangle = \langle \psi | A | \psi \rangle\) 被混合态下的 \[ \langle A \rangle = \operatorname{tr} (\rho A)~ \] 所替代。[8]: 73 

　　 此外，如果 \(A\) 具有谱分解 \[ A = \sum_i a_i P_i~ \] 其中，\(P_i\) 是对应于特征值 \(a_i\) 的投影算符，那么测量后的密度算符为[12][13] \[ \rho_i' = \frac{P_i \rho P_i}{\operatorname{tr}[\rho P_i]}~ \] 当测量结果为 \(i\) 时获得。在测量结果未知的情况下，集合则描述为 \[ \rho' = \sum_i P_i \rho P_i~ \] 如果假设测量结果的概率是投影算符 \(P_i\) 的线性函数，那么它们必须通过投影算符与密度算符的迹运算给出。Gleason 定理表明，在三维或更高维的希尔伯特空间中，线性假设可以替换为非情境性假设。[14] 这种维度上的限制可以通过假设 POVM（正交投影测量算符）也具备非情境性来去除，[15][16] 但这一点被批评为在物理上缺乏动机。[17]

5. 熵（Entropy）

　　 冯·诺依曼熵（von Neumann entropy）\( S \) 的混合态可以通过密度算符 \(\rho\) 的特征值，或者通过密度算符 \(\rho\) 的迹与对数来表示。由于密度算符 \(\rho\) 是一个半正定算符，它具有谱分解形式：\(\rho = \sum_i \lambda_i |\varphi_i \rangle \langle \varphi_i|,\) 其中 \(|\varphi_i\rangle\) 是正交归一的向量，\(\lambda_i \geq 0\)，并且 \(\sum_i \lambda_i = 1\)。那么，量子系统的熵为： \[ S = - \sum_i \lambda_i \ln \lambda_i = - \operatorname{tr}(\rho \ln \rho).~ \] 这个定义意味着，任何纯态的冯·诺依曼熵都是零。[18]: 217 如果 \(\rho_i\) 是支持在正交子空间上的态，那么这些态的凸组合的冯·诺依曼熵为： \[ \rho = \sum_i p_i \rho_i,~ \] 其冯·诺依曼熵为这些态的冯·诺依曼熵和概率分布 \( p_i \) 的香农熵的和： \[ S(\rho) = H(p_i) + \sum_i p_i S(\rho_i).~ \] 当态 \(\rho_i\) 没有正交支持时，右边的和严格大于凸组合态 \(\rho\) 的冯·诺依曼熵。[6]: 518 

　　 给定一个密度算符 \(\rho\) 和一个项目测量，如前所述，定义的态 \(\rho'\) 由如下凸组合表示： \[ \rho' = \sum_i P_i \rho P_i,~ \] 这个可以解释为执行测量后，未记录发生了哪个结果所产生的态，[9]: 159 其冯·诺依曼熵大于 \(\rho\) 的熵，除非 \(\rho = \rho'\)。然而，通过广义测量或 POVM 所产生的 \(\rho'\) 可能会具有比 \(\rho\) 更低的冯·诺依曼熵。[6]: 514 

6. 冯·诺依曼方程的时间演化

　　 就像薛定谔方程描述了纯态如何随时间演化一样，冯·诺依曼方程（也称为李维尔-冯·诺依曼方程）描述了密度算符如何随时间演化。冯·诺依曼方程规定： \[ i\hbar \frac{\operatorname{d} \rho}{\operatorname{d} t} = [H, \rho]~,~ \] 其中，方括号表示对易子。

　　 该方程仅在密度算符处于薛定谔图像下成立，尽管这个方程看起来一开始像是模拟海森堡图像中的海森堡方程，具有一个关键的符号差异： \[ i\hbar \frac{\operatorname{d} A^{(\mathrm{H})}}{\operatorname{d} t} = -[H, A^{(\mathrm{H})}]~,~ \] 其中 \( A^{(\mathrm{H})}(t) \) 是某个海森堡图像下的算符；但在这个图像下，密度矩阵并不随时间变化，而相对符号的差异确保了期望值 \( \langle A \rangle \) 的时间导数与薛定谔图像中的结果相同。[5]

　　 如果哈密顿量是时间不变的，那么冯·诺依曼方程可以轻松求解，得到： \[ \rho(t) = e^{-iHt/\hbar} \rho(0) e^{iHt/\hbar}.~ \] 对于更一般的哈密顿量，如果 \( G(t) \) 是某个区间内的波函数传播子，那么密度矩阵在该区间内的时间演化由以下公式给出： \[ \rho(t) = G(t) \rho(0) G(t)^{\dagger}.~ \]

7. Wigner 函数和经典类比

　　 密度矩阵算符也可以在相空间中实现。在 Wigner 映射下，密度矩阵变换为等效的 Wigner 函数： \[ W(x,p) \stackrel{\mathrm{def}}{=} \frac{1}{\pi \hbar} \int_{-\infty}^{\infty} \psi^*(x+y)\psi(x-y) e^{2ipy/\hbar} \, dy.~ \] Wigner 函数的时间演化方程，被称为 Moyal 方程，是上述冯·诺依曼方程的 Wigner 变换： \[ \frac{\partial W(x,p,t)}{\partial t} = -\{\{W(x,p,t), H(x,p)\}\},~ \] 其中 \( H(x,p) \) 是哈密顿量，\(\{\{\cdot, \cdot \}\}\) 是 Moyal 括号，是量子对易子的变换。

　　 Wigner 函数的演化方程与其经典极限，即经典物理中的李维尔方程相似。在普朗克常数 \(\hbar\) 趋近于零的极限下，\( W(x,p,t) \) 退化为经典相空间中的李维尔概率密度函数。

8. 示例应用

　　 密度矩阵是量子力学的基础工具，几乎在任何类型的量子力学计算中都会至少偶尔出现。以下是一些密度矩阵特别有用且常见的具体应用示例：

• 统计力学使用密度矩阵，最突出的应用是表示系统在非零温度下的准备状态。通过使用典型系综构造密度矩阵得到的结果形式为：\([\rho = \frac{ \exp\left(-\beta H\right) }{Z(\beta)},\) 其中 \( \beta \) 是逆温度 \( (k_B T)^{-1} \)，而 \( H \) 是系统的哈密顿量。归一化条件要求密度矩阵的迹等于 1，这样就定义了配分函数为：\(Z(\beta) = \mathrm{tr} \exp\left(-\beta H\right) .\) 如果系统中粒子的数量不确定，则可以应用大正则系综，其中用来求和构造密度矩阵的状态来自于 Fock 空间。[22]: 174 
• 量子去相干理论通常涉及非孤立的量子系统与其他系统（包括测量设备）之间的纠缠发展。密度矩阵使得描述这一过程并计算其后果变得更加容易。量子去相干解释了为什么一个与环境相互作用的系统会从纯态（展示叠加态）过渡到混合态（经典选择的无序组合）。这一过渡本质上是可逆的，因为系统和环境的合成态仍然是纯态，但在实践中不可逆，因为环境是一个非常大且复杂的量子系统，无法逆转它们之间的相互作用。因此，去相干对解释量子力学的经典极限非常重要，但无法解释波函数坍缩，因为在混合态中所有经典选择仍然存在，而波函数坍缩只选择其中的一个。[23]
• 类似地，在量子计算、量子信息理论、开放量子系统以及其他涉及状态制备噪声和可能发生去相干的领域，密度矩阵被频繁使用。噪声通常通过去极化通道或幅度衰减通道进行建模。**量子断层扫描** 是一个过程，通过给定一组代表量子测量结果的数据，计算与这些测量结果一致的密度矩阵。[24][25]
• 在分析多电子系统（如原子或分子）时，一个不完全但有用的初步近似是将电子视为不相关的，或者每个电子都具有独立的单粒子波函数。这通常是构建 Hartree–Fock 方法中 Slater 行列式的起点。如果有 \( N \) 个电子填充 \( N \) 个单粒子波函数 \( |\psi_i \rangle \)，那么这 \( N \) 个电子的集合可以通过密度矩阵表示为：\(\sum_{i=1}^{N} |\psi_i \rangle \langle \psi_i |.\)

9. C*-代数的态的表述

　　 现在普遍认为，量子力学的描述中，所有自伴算符都代表可观测量的观点是不可持续的。[26][27] 因此，可观测量被确定为抽象 C*-代数 \( A \) 的元素（即没有作为算符代数的特殊表示），而态则是 \( A \) 上的正线性泛函。然而，通过使用 GNS 构造方法，我们可以恢复出使 \( A \) 成为算符子代数的希尔伯特空间。

　　 从几何角度看，C*-代数 \( A \) 上的纯态是所有状态集合的极点。根据 GNS 构造的性质，这些态对应于 \( A \) 的不可约表示。

　　 紧算符代数 \( K(H) \) 的态恰好对应于密度算符，因此 \( K(H) \) 的纯态正是量子力学意义上的纯态。

　　 C*-代数的表述可以看作是包括经典和量子系统的。当系统是经典时，观测量的代数变成了阿贝尔 C*-代数。在这种情况下，态变成了概率测度。

10. 历史

　　 密度算符和密度矩阵的形式主义由约翰·冯·诺依曼（John von Neumann）于 1927 年提出[28]，并且由列夫·朗道（Lev Landau）独立提出，但后者的系统性较差[29]，在 1946 年，费利克斯·布洛赫（Felix Bloch）也进行了相关的提出[30]。冯·诺依曼引入密度矩阵的目的是为了发展量子统计力学和量子测量理论。密度矩阵这个名字本身与它在经典统计力学中对应的相空间概率度量（位置和动量的概率分布）相关，这种度量由维格纳（Wigner）于 1932 年引入[3]。

　　 与此不同，朗道提出密度矩阵的动机是因为无法用态矢量描述复合量子系统的一个子系统[29]。

11. 参见

• 原子电子跃迁
• 密度泛函理论
• 格林-库博关系
• 格林函数（多体理论）
• 林布拉德方程
• 维格纳准概率分布

12. 注释和参考文献

1. Shankar, Ramamurti (2014). *Principles of Quantum Mechanics* (第 2 版，[第 19 次修订版]). 纽约, NY: Springer. ISBN 978-0-306-44790-7.
2. Ballentine, Leslie (2009). "Density Matrix". *Compendium of Quantum Physics*. 柏林, 海德堡: Springer Berlin Heidelberg. 第 166 页. doi:10.1007/978-3-540-70626-7_51. ISBN 978-3-540-70622-9.
3. Fano, U. (1957). "Description of States in Quantum Mechanics by Density Matrix and Operator Techniques". *Reviews of Modern Physics*. 29 (1): 74–93. Bibcode:1957RvMP...29...74F. doi:10.1103/RevModPhys.29.74.
4. Holevo, Alexander S. (2001). *Statistical Structure of Quantum Theory*. Lecture Notes in Physics. Springer. ISBN 3-540-42082-7. OCLC 318268606.
5. Hall, Brian C. (2013). "Systems and Subsystems, Multiple Particles". *Quantum Theory for Mathematicians*. Graduate Texts in Mathematics. 第 267 卷. 第 419–440 页. doi:10.1007/978-1-4614-7116-5_19. ISBN 978-1-4614-7115-8.
6. Nielsen, Michael; Chuang, Isaac (2000). *Quantum Computation and Quantum Information*. 剑桥大学出版社. ISBN 978-0-521-63503-5.
7. Davidson, Ernest Roy (1976). *Reduced Density Matrices in Quantum Chemistry*. Academic Press, London.
8. Peres, Asher (1995). *Quantum Theory: Concepts and Methods*. Kluwer. ISBN 978-0-7923-3632-7. OCLC 901395752.
9. Wilde, Mark M. (2017). *Quantum Information Theory* (第 2 版). 剑桥大学出版社. arXiv:1106.1445. doi:10.1017/9781316809976.001. ISBN 978-1-107-17616-4. OCLC 973404322. S2CID 2515538.
10. Kirkpatrick, K. A. (2006 年 2 月). "The Schrödinger-HJW Theorem". *Foundations of Physics Letters*. 19 (1): 95–102. arXiv:quant-ph/0305068. Bibcode:2006FoPhL..19...95K. doi:10.1007/s10702-006-1852-1. ISSN 0894-9875. S2CID 15995449.
11. Ochs, Wilhelm (1981 年 11 月 1 日). "Some comments on the concept of state in quantum mechanics". *Erkenntnis*. 16 (3): 339–356. doi:10.1007/BF00211375. ISSN 1572-8420. S2CID 119980948.
12. Lüders, Gerhart (1950). "Über die Zustandsänderung durch den Messprozeß". *Annalen der Physik*. 443 (5–8): 322. Bibcode:1950AnP...443..322L. doi:10.1002/andp.19504430510. 由 K. A. Kirkpatrick 翻译为 Lüders, Gerhart (2006 年 4 月 3 日). "Concerning the state-change due to the measurement process". *Annalen der Physik*. 15 (9): 663–670. arXiv:quant-ph/0403007. Bibcode:2006AnP...518..663L. doi:10.1002/andp.200610207. S2CID 119103479.
13. Busch, Paul; Lahti, Pekka (2009), Greenberger, Daniel; Hentschel, Klaus; Weinert, Friedel (编辑), "Lüders Rule", *Compendium of Quantum Physics*, Springer Berlin Heidelberg, 第 356–358 页, doi:10.1007/978-3-540-70626-7_110, ISBN 978-3-540-70622-9
14. Gleason, Andrew M. (1957). "Measures on the closed subspaces of a Hilbert space". *Indiana University Mathematics Journal*. 6 (4): 885–893. doi:10.1512/iumj.1957.6.56050. MR 0096113.
15. Busch, Paul (2003). "Quantum States and Generalized Observables: A Simple Proof of Gleason's Theorem". *Physical Review Letters*. 91 (12): 120403. arXiv:quant-ph/9909073. Bibcode:2003PhRvL..91l0403B. doi:10.1103/PhysRevLett.91.120403. PMID 14525351. S2CID 2168715.
16. Caves, Carlton M.; Fuchs, Christopher A.; Manne, Kiran K.; Renes, Joseph M. (2004). "Gleason-Type Derivations of the Quantum Probability Rule for Generalized Measurements". *Foundations of Physics*. 34 (2): 193–209. arXiv:quant-ph/0306179. Bibcode:2004FoPh...34..193C. doi:10.1023/B:FOOP.0000019581.00318.a5. S2CID 18132256.
17. Andrzej Grudka; Paweł Kurzyński (2008). "Is There Contextuality for a Single Qubit?". *Physical Review Letters*. 100 (16): 160401. arXiv:0705.0181. Bibcode:2008PhRvL.100p0401G. doi:10.1103/PhysRevLett.100.160401. PMID 18518167. S2CID 13251108.
18. Rieffel, Eleanor G.; Polak, Wolfgang H. (2011 年 3 月 4 日). *Quantum Computing: A Gentle Introduction*. MIT Press. ISBN 978-0-262-01506-6.
19. Breuer, Heinz; Petruccione, Francesco (2002). *The theory of open quantum systems*, Oxford University Press, 第 110 页, ISBN 978-0-19-852063-4.
20. Schwabl, Franz (2002). *Statistical mechanics*, Springer, 第 16 页, ISBN 978-3-540-43163-3.
21. Müller-Kirsten, Harald J.W. (2008). *Classical Mechanics and Relativity*, World Scientific, 第 175–179 页, ISBN 978-981-283-251-1.
22. Kardar, Mehran (2007). *Statistical Physics of Particles*. Cambridge University Press. ISBN 978-0-521-87342-0. OCLC 860391091.
23. Schlosshauer, M. (2019). "Quantum Decoherence". *Physics Reports*. 831: 1–57. arXiv:1911.06282. Bibcode:2019PhR...831....1S. doi:10.1016/j.physrep.2019.10.001. S2CID 208006050.
24. Granade, Christopher; Combes, Joshua; Cory, D. G. (2016 年 1 月 1 日). "Practical Bayesian tomography". *New Journal of Physics*. 18 (3): 033024. arXiv:1509.03770. Bibcode:2016NJPh...18c3024G. doi:10.1088/1367-2630/18/3/033024. ISSN 1367-2630. S2CID 88521187.
25. Ardila, Luis; Heyl, Markus; Eckardt, André (2018 年 12 月 28 日). "Measuring the Single-Particle Density Matrix for Fermions and Hard-Core Bosons in an Optical Lattice". *Physical Review Letters*. 121 (260401): 6. arXiv:1806.08171. Bibcode:2018PhRvL.121z0401P. doi:10.1103/PhysRevLett.121.260401. PMID 30636128. S2CID 51684413.
26. 见附录，Mackey, George Whitelaw (1963). *Mathematical Foundations of Quantum Mechanics*, Dover Books on Mathematics, New York: Dover Publications, ISBN 978-0-486-43517-6.
27. Emch, Gerard G. (1972). *Algebraic Methods in Statistical Mechanics and Quantum Field Theory*, Wiley-Interscience, ISBN 978-0-471-23900-0.
28. von Neumann, John (1927). "Wahrscheinlichkeitstheoretischer Aufbau der Quantenmechanik", *Göttinger Nachrichten*, 1: 245–272. "The Damping Problem in Wave Mechanics (1927)". *Collected Papers of L.
29. D. Landau*. 1965. pp. 8–18. doi:10.1016/B978-0-08-010586-4.50007-9. ISBN 978-0-08-010586-4.
30. Fano, Ugo (1995). "Density Matrices as Polarization Vectors". *Rendiconti Lincei*. 6 (2): 123–130. doi:10.1007/BF03001661. S2CID 128081459.