庞加莱猜想（综述）

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 在几何拓扑的数学领域，庞加莱猜想（英国发音：/ˈpwæ̃kæreɪ/，美国发音：/ˌpwæ̃kɑːˈreɪ/，法语发音：[pwɛ̃kaʁe]）是一个关于 3-球体的定理，3-球体是四维空间中界定单位球的超球面。

　　 该猜想最初由亨利·庞加莱于 1904 年提出，定理涉及到一些局部上看起来像普通三维空间，但在规模上是有限的空间。庞加莱假设，如果这样的空间具有一个额外的特性，即该空间中的每一条环路都可以连续地收缩到一个点，那么这个空间必定是一个三维球体。解决该猜想的努力推动了 20 世纪几何拓扑领域的许多进展。

　　 最终的证明基于理查德·S·汉密尔顿使用 Ricci 流来解决该问题的方案。通过在 Ricci 流理论中发展一系列新的技术和结果，格里戈里·佩雷尔曼能够修改并完成汉密尔顿的方案。在 2002 年和 2003 年发布于 arXiv 的论文中，佩雷尔曼展示了他证明庞加莱猜想（以及威廉·瑟尔斯顿的更强的几何化猜想）工作的过程。随后几年，几位数学家研究了他的论文，并详细阐述了他的工作。

　　 汉密尔顿和佩雷尔曼在该猜想上的工作被广泛认为是数学研究的一个里程碑。汉密尔顿因其贡献获得了邵逸夫奖和勒罗伊·P·斯蒂尔研究奠基奖。《科学》杂志将佩雷尔曼证明庞加莱猜想的成果评为 2006 年年度科学突破。[5] 克雷数学研究所将庞加莱猜想列为著名的千年奖问题之一，并为该猜想的解决提供了 100 万美元的奖赏。[6] 佩雷尔曼拒绝了这一奖项，称汉密尔顿的贡献与他自己的贡献相等。[7][8]

1. 概述

　　 庞加莱猜想是几何拓扑学领域的一个数学问题。用该领域的术语来说，它表述如下：

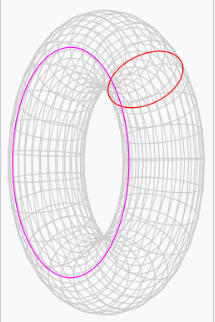
　　 庞加莱猜想： 每一个封闭、连通且基本群为平凡的三维拓扑流形，与三维球面是同胚的。

　　 熟悉的形状，比如球体的表面（在数学中称为二维球面）或环面的表面，都是二维的。球体的表面具有平凡的基本群，意味着在表面上画出的任何环都可以连续地变形为一个点。相比之下，环面的表面具有非平凡的基本群，因为表面上存在一些环无法这样变形。两者都是拓扑流形，且都是闭合的（意味着它们没有边界，占据有限的空间区域）和连通的（意味着它们由一个整体组成）。当两个闭合流形的点能够通过连续的方式重新映射到彼此时，称它们是同胚的。由于基本群的（非）平凡性在同胚变换下是不变的，因此可以推断二维球面和环面不是同胚的。

　　 庞加莱猜想的二维类比表明，任何闭合且连通的二维拓扑流形，如果不是二维球面同胚的，则必定包含一个无法连续收缩为一点的环。（这可以通过环面的例子来说明，如上所述。）通过对闭合且连通的二维拓扑流形的分类，已知这一类比是成立的，早在 19 世纪 60 年代就以各种形式被理解。在更高维度中，闭合且连通的拓扑流形没有简单的分类方法，这使得庞加莱猜想的解决变得更加复杂。

2. 历史

庞加莱的问题

　　 在 19 世纪，伯恩哈德·黎曼和恩里科·贝蒂开始研究流形的拓扑不变量。[9][10] 他们引入了贝蒂数，它将每个流形与一组非负整数关联起来。黎曼曾证明，闭合且连通的二维流形可以通过其贝蒂数完全表征。在他的 1895 年论文《分析位置》（于 1892 年公布）中，庞加莱证明了黎曼的结果无法扩展到更高维度。[11][12][13] 为此，他引入了基本群作为一种新的拓扑不变量，并能够展示一些具有相同贝蒂数但不同基本群的三维流形的例子。他提出了一个问题：基本群是否足以在拓扑上表征一个流形（给定维度），尽管他并没有继续追求答案，仅仅表示这将 “需要漫长且困难的研究”。[12][13][14]

　　 庞加莱论文的主要目的是通过他新引入的同调群来解释贝蒂数，并提出关于贝蒂数对称性的庞加莱对偶定理。在他遭到对论证完整性的批评后，他发布了若干后续的 “补充” 来增强和修正他的工作。他的第二篇补充材料，发表于 1900 年，最后写道：[15][13]

　　 “为了避免使这项工作过于冗长，我仅限于陈述以下定理，证明将需要进一步的发展：

　　 每个所有贝蒂数都等于 1 且所有其 Tq 表可定向的多面体都是简单连通的，即同胚于超球面。”

　　 （用现代的语言来说，考虑到庞加莱在使用简单连通性的术语时有一种不常见的方式[16]，这句话的意思是：一个具有球面同调群的闭合连通定向流形必须同胚于一个球面。[14]）这两点对庞加莱对黎曼工作的否定性推广做出了两方面的修改。首先，他现在使用了完整的同调群，而不仅仅是贝蒂数。其次，他将问题的范围从询问任意流形是否由拓扑不变量来表征，缩小到询问球面是否可以这样被表征。

　　 然而，在出版后，庞加莱发现他宣布的定理是错误的。在他 1904 年发布的第五篇也是最后一篇补充中，他通过庞加莱同调球的反例证明了这一点。庞加莱同调球是一个闭合连通的三维流形，它具有与球面相同的同调群，但其基本群有 120 个元素。这个例子清楚地表明，同调群不足以表征流形的拓扑结构。在第五篇补充的结束语中，庞加莱修改了他错误的定理，改用基本群代替同调群：[17][13]

　　 “有一个问题仍需解决：是否有可能流形 V 的基本群缩减为单位元素，而 V 却不是简单连通的？[...] 然而，这个问题将把我们带得太远。”

　　 在这个备注中，和第二篇补充的结束语一样，庞加莱使用了 “简单连通” 这个术语的方式与现代用法不一致，并且与他 1895 年对该术语的定义相矛盾。[12][16]（根据现代用法，庞加莱的问题是自明的，问的是是否有可能一个流形是简单连通的却不是简单连通的。）然而，正如从上下文中可以推断的那样，[18]庞加莱的真正问题是：基本群的平凡性是否能够唯一地表征球面。[14]

　　 在黎曼、贝蒂和庞加莱的工作中，所涉及的拓扑概念并没有以现代视角下精确的方式定义或使用。即便是 “流形” 这一关键概念，在庞加莱自己的工作中也没有一致的使用方式，并且常常混淆了拓扑流形、分段线性（PL）流形和平滑流形的概念。[16][19]因此，我们无法毫无歧义地解读庞加莱提出的问题。只有通过后来的数学家们对拓扑学的形式化和词汇发展，庞加莱的最后问题才被理解为 “庞加莱猜想”，如前文所述。

　　 然而，尽管通常将其表述为一个猜想，提出所有某类流形都是与球面同胚的，但庞加莱只是提出了一个开放性的问题，并未尝试猜测答案的方向。此外，没有证据表明他相信自己的问题会以何种方式得到回答。[14]

解答

　　 在 20 世纪 30 年代，J.H.C.怀特海德声称已证明此猜想，但后来撤回了证明。在此过程中，他发现了一些简单连通的（实际上是收缩的，即同伦理等价于一个点的）非紧致 3 流形，它们与 ${\mathbb{R}}^3$ 不同，现今称为怀特海德流形。

　　 在 20 世纪 50 至 60 年代，其他数学家尝试证明该猜想，但都发现其证明存在缺陷。诸如乔治·德·拉姆（Georges de Rham）、R.H.宾（R.H. Bing）、沃尔夫冈·哈肯（Wolfgang Haken）、埃德温·莫伊斯（Edwin E. Moise）和基里斯托斯·帕帕基里亚科普洛斯（Christos Papakyriakopoulos）等有影响力的数学家也尝试过证明该猜想。1958 年，R.H.宾证明了庞加莱猜想的一个弱版本：如果一个紧致的 3 流形的每一个简单闭合曲线都包含在一个 3 球内，那么该流形与 3 球同胚。[20]宾还描述了尝试证明庞加莱猜想时的一些陷阱。[21]

　　 1978 年，Włodzimierz Jakobsche 证明，如果宾-博尔苏克猜想在 3 维下成立，那么庞加莱猜想也必须成立。[22]

　　 随着时间的推移，庞加莱猜想被认为特别难以攻克。约翰·米尔诺（John Milnor）评论说，有时错误的证明中的漏洞 “相当微妙，且难以察觉”。[23]对该猜想的研究提高了对 3 流形的理解。该领域的专家往往不愿宣布证明，并且倾向于对任何此类声明持怀疑态度。20 世纪 80 至 90 年代，出现了一些广为宣传的错误证明（这些证明实际上并未以同行评审的形式发表）。[24][25]

　　 关于尝试证明这一猜想的过程，可以在乔治·斯皮罗（George Szpiro）的非技术性著作《庞加莱的奖赏》（Poincaré's Prize）中找到详细的阐述。[26]

维度

　　 闭合曲面的分类给出了二维情况的类比问题的肯定答案。对于三维以上的情况，可以提出广义庞加莱猜想：同伦理 n-球是否与 n-球同胚？比简单连通性更强的假设是必要的；在四维及更高维度中，存在简单连通的闭合流形，它们与 n-球在同伦理下并不等价。

　　 历史上，尽管三维的庞加莱猜想似乎是合理的，但广义猜想曾被认为是错误的。1961 年，斯蒂芬·斯梅尔（Stephen Smale）通过证明四维及更高维度的广义庞加莱猜想震惊了数学界，并扩展了他的技术来证明基本的 h-同调定理。1982 年，迈克尔·弗里德曼（Michael Freedman）证明了四维的庞加莱猜想。弗里德曼的工作尚未排除四维中存在一个与四维球同胚，但与其不同构的光滑四流形的可能性。这个所谓的四维光滑庞加莱猜想仍然是开放问题，并且被认为是非常困难的。例如，米尔诺（Milnor）的异质球体证明了光滑庞加莱猜想在七维下是错误的。

　　 这些早期在更高维度上的成功让三维的情况悬而未决。庞加莱猜想在四维和所有更高维度中基本上是正确的，原因各不相同。在三维情况下，直到几何化猜想将其置于所有 3 流形的框架中，庞加莱猜想的声誉才变得明确。约翰·摩根（John Morgan）写道：[27]

　　 “在瑟斯顿关于双曲 3 流形的工作以及……几何化猜想之前，我认为专家们并没有就庞加莱猜想的真伪达成共识。瑟斯顿的工作之后，尽管它与庞加莱猜想没有直接关系，但专家们形成了一种共识：庞加莱猜想（以及几何化猜想）是正确的。”

哈密尔顿的计划和解决方案

　　 哈密尔顿的计划始于他 1982 年的论文，在这篇论文中他引入了流形上的 Ricci 流，并展示了如何利用它证明庞加莱猜想的一些特例。[28] 在接下来的几年里，他扩展了这项工作，但未能证明该猜想。直到格里戈里·佩雷尔曼发表了他的论文，实际的解决方案才得以找到。

　　 2002 年底和 2003 年，佩雷尔曼在 arXiv 上发布了三篇论文。[29][30][31] 在这些论文中，他勾画了庞加莱猜想的证明以及一个更一般的猜想——索斯顿的几何化猜想，完成了理查德·S·哈密尔顿早期概述的 Ricci 流计划。

　　 从 2006 年 5 月到 7 月，几个小组发表了论文，填补了佩雷尔曼对庞加莱猜想证明的细节，具体如下：

• 布鲁斯·克莱纳和约翰·W·洛特于 2006 年 5 月在 arXiv 上发布了一篇论文，填补了佩雷尔曼对几何化猜想证明的细节，这些细节基于自 2003 年以来已公开的部分版本。[32] 他们的手稿于 2008 年在《几何与拓扑》期刊上发表。2011 年和 2013 年进行了少量修正；例如，他们发表论文的第一版使用了哈密尔顿关于 Ricci 流的紧性定理的一个不正确版本。
• 曹怀东和朱西平于 2006 年 6 月在《亚洲数学杂志》上发表了一篇论文，阐述了庞加莱猜想和几何化猜想的完整证明。[33] 他们论文的开头段落写道：
  在本文中，我们将展示哈密尔顿-佩雷尔曼的 Ricci 流理论。基于此，我们将首次提供庞加莱猜想和索斯顿几何化猜想的完整证明。虽然完整的工作是许多几何分析学者的共同努力，但主要贡献者无疑是哈密尔顿和佩雷尔曼。
  一些观察者认为曹和朱在将佩雷尔曼的工作归功于自己。随后，他们在 arXiv 上发布了修订版，改变了措辞。[34] 此外，他们的论文中有一页内容与克莱纳和洛特早期公开版本的其中一页几乎相同；这一点也在修订版中进行了修改，并且得到了期刊编辑委员会的道歉。
  
• 约翰·摩根和江天于 2006 年 7 月在 arXiv 上发布了一篇论文，给出了庞加莱猜想的详细证明（这比完整的几何化猜想稍微容易一些）[35]，并将其扩展为一本书。[36][37]

　　 三个小组都发现，佩雷尔曼论文中的空白是微不足道的，可以通过他自己的方法填补。

　　 2006 年 8 月 22 日，国际数学大会（ICM）因佩雷尔曼在 Ricci 流方面的工作授予他菲尔兹奖，但佩雷尔曼拒绝了这一奖项。[38][39] 约翰·摩根于 2006 年 8 月 24 日在 ICM 上发表了关于庞加莱猜想的演讲，宣称 “在 2003 年，佩雷尔曼解决了庞加莱猜想”。[40]

　　 2006 年 12 月，《科学》杂志将庞加莱猜想的证明评为 “年度突破”，并将其作为封面故事。[5]

3. Ricci 流与手术

　　 哈密尔顿证明庞加莱猜想的计划首先是为未知的简单连通闭合 3 流形上放置一个黎曼度量。基本的思想是尝试‘改善’这个度量；例如，如果可以改进度量，使其具有常数正曲率，那么根据黎曼几何学中的经典结果，它必须是三维球面。哈密尔顿为改进度量规定了‘Ricci 流方程’： $${\partial }_t{g}_{ij}=-2R_{ij}$$ 其中 $g$ 是度量，$R$ 是其 Ricci 曲率，人们希望随着时间 $t$ 的增加，流形变得更加容易理解。Ricci 流扩展流形的负曲率部分，并收缩正曲率部分。

　　 在某些情况下，哈密尔顿能够证明这一方法有效；例如，他的原始突破是证明，如果黎曼流形的 Ricci 曲率处处为正，那么上述过程只能在一个有界的参数值区间内进行， $t\in [0,T)$ 且 $T<\mathrm{\infty }$，更重要的是，存在某些数值 $c_t$，使得随着 $t\nearrow T$，黎曼度量 $c_{t}g(t)$ 平滑地收敛到常数正曲率的度量。根据经典的黎曼几何学，唯一可以支持常数正曲率黎曼度量的简单连通紧致流形是球面。因此，实际上，哈密尔顿证明了庞加莱猜想的一个特例：如果一个紧致的简单连通 3 流形支持正 Ricci 曲率的黎曼度量，那么它必定是三维球面。

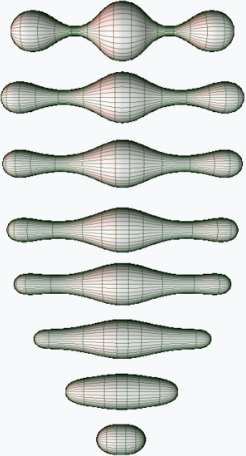
　　 如果仅仅拥有一个任意的黎曼度量，Ricci 流方程则必然会导致更复杂的奇异性。佩雷尔曼的主要成就是证明了，如果从某种角度来看，如果这些奇异性在有限时间内出现，它们只能表现为收缩的球面或圆柱体。通过对这一现象的定量理解，他沿着奇异性对流形进行切割，将流形分成几个部分，然后在这些部分上继续进行 Ricci 流。这个过程被称为带有手术的 Ricci 流。

　　 佩雷尔曼提供了一个基于曲线收缩流的独立论证，证明在一个简单连通的紧致 3 流形上，任何带有手术的 Ricci 流解在有限时间内都会消失。托比亚斯·科尔丁和威廉·米尼科齐提供了一个基于最小曲面和几何测度论的最小-最大理论的替代论证。因此，在简单连通的背景下，带有手术的 Ricci 流的上述有限时间现象就是所有相关内容。事实上，即使基本群是有限群和循环群的自由积，这一点也成立。

　　 这个关于基本群的条件证明是有限时间消失的必要且充分条件。它等价于说，流形的素分解没有非解环分量，并且证明等价于所有几何部分的流形都具有基于两种索斯顿几何——$S^2\times R$ 和 $S^3$ 的几何。对于不对基本群做任何假设的情况，佩雷尔曼进一步进行了关于流形在无限大时间下的极限的技术研究，并在此过程中证明了索斯顿的几何化猜想：在大时间下，流形具有厚薄分解，其中厚部分具有双曲几何结构，薄部分是图流形。然而，由于佩雷尔曼和科尔丁、米尼科齐的结果，这些进一步的结果在证明庞加莱猜想时并不必要。

4. 解

　　 2002 年 11 月 11 日，俄罗斯数学家格里高利·佩雷尔曼在 arXiv 上发布了第一篇系列三篇论文，概述了庞加莱猜想的解答。佩雷尔曼的证明使用了理查德·S·汉密尔顿开发的改进版 Ricci 流程序。2006 年 8 月，佩雷尔曼因其在 Ricci 流方面的工作被授予但拒绝了菲尔兹奖（价值 15000 加元）。2010 年 3 月 18 日，克莱数学研究所因佩雷尔曼的证明向他授予了 100 万美元的千年奖，以表彰他的成就。佩雷尔曼也拒绝了这一奖项。

　　 佩雷尔曼通过使用 Ricci 流变形流形来证明了该猜想（Ricci 流类似于描述热量通过物体扩散的热方程）。Ricci 流通常将流形变形为更圆的形状，除了在一些情况下，它会将流形拉伸并远离自身，朝向被称为奇点的地方。佩雷尔曼和汉密尔顿随后在奇点处切割流形（这一过程称为 “手术”），使得分离的部分形成球形。证明中的主要步骤包括展示流形在 Ricci 流变形下的行为，检查会发展出什么样的奇点，确定这个手术过程是否可以完成，并证明该手术不需要无限次重复。

　　 第一步是使用 Ricci 流变形流形。Ricci 流由理查德·S·汉密尔顿定义，作为一种变形流形的方法。Ricci 流的公式模仿了热方程，后者描述了热量在固体中流动的方式。像热流一样，Ricci 流趋向于均匀行为。与热流不同，Ricci 流可能会遇到奇点并停止运作。流形中的奇点是指在该点无法微分的地方：比如角落、尖点或压缩点。Ricci 流仅在光滑可微流形上定义。汉密尔顿使用 Ricci 流证明了某些紧致流形是同胚于球面的，并且他希望将其应用于证明庞加莱猜想。他需要理解奇点的性质。

　　 汉密尔顿列出了可能形成的奇点，但他担心某些奇点可能会导致困难。他想在奇点处切割流形并加上帽子，然后再次运行 Ricci 流，因此他需要理解奇点并证明某些类型的奇点不会出现。佩雷尔曼发现这些奇点都非常简单：考虑一个圆柱体是通过在另一个维度中沿一条线 “拉伸” 一个圆形成的，用球体代替圆重复这一过程，实际上就得到了奇点的形态。佩雷尔曼通过一种叫做 “简化体积” 的方法证明了这一点，简化体积与某个椭圆方程的特征值密切相关。

　　 有时候，其他复杂的运算会简化为与标量（一个数）的乘法。这样的数被称为该运算的特征值。特征值与振动频率密切相关，并且常用于分析一个著名的问题：你能听到鼓的形状吗？从本质上讲，特征值就像流形发出的音符。佩雷尔曼证明了随着流形被 Ricci 流变形，这个音符会增大。这帮助他排除了一些汉密尔顿曾担心的麻烦奇点，特别是雪茄状孤子解，它看起来像一根从流形中突出、另一侧没有任何东西的长条。实际上，佩雷尔曼证明了所有形成的长条都可以被切割和加帽，并且没有任何一端只突出一边。

　　 完成证明后，佩雷尔曼取任何一个没有边界的紧致单连通三维流形，并开始运行 Ricci 流。这将流形变形成圆形块状，块与块之间有长条连接。他切割这些长条，继续变形流形，直到最终留下一个由圆形三维球体组成的集合。然后，他通过将这些球体用三维圆柱体连接起来，重建原始流形，将它们变形成圆形，并发现，尽管最初有许多混乱，流形实际上是同胚于球体的。

　　 一个立即出现的问题是如何确保不需要进行无限次切割。这个问题是由于切割可能会永远进行下去。佩雷尔曼通过使用流形上的最小曲面证明了这种情况不可能发生。最小曲面是指任何局部变形都会增加面积的曲面；一个熟悉的例子是横跨弯曲的金属丝圈的肥皂膜。汉密尔顿曾证明，随着流形经历 Ricci 流，最小曲面的面积会减少。佩雷尔曼验证了流形被切割时最小曲面面积的变化。他证明，最终，面积会变得非常小，任何在面积变小后进行的切割，只能是切割三维球体，而不是更复杂的部分。Sormani 在 Szpiro 的书中提到这部分证明时，将其比作与海多拉的斗争。这部分证明出现在佩雷尔曼关于该主题的第三篇也是最后一篇论文中。

5. 另见

• 《流形的命运》

6. 参考文献

1. Matveev, Sergei (2007). "1.3.4 Zeeman's Collapsing Conjecture". 《算法拓扑与三维流形的分类》. 《算法与计算在数学中的应用》. 第 9 卷. 施普林格. 第 46-58 页. ISBN 978-3540458999.
2. "Poincaré, Jules-Henri". 《Lexico UK English Dictionary》. 牛津大学出版社. 原文存档于 2022-09-02.
3. "Poincaré". 《The American Heritage Dictionary of the English Language》（第 5 版）. 哈珀·柯林斯. 2019 年 8 月 9 日检索.
4. "Poincaré". 《Merriam-Webster.com Dictionary》. 梅里亚姆-韦伯斯特. 2019 年 8 月 9 日检索.
5. Mackenzie, Dana (2006-12-22). "The Poincaré Conjecture – Proved". 《科学》. 314 (5807): 1848–1849. doi:10.1126/science.314.5807.1848. PMID 17185565. S2CID 121869167.
6. "解答庞加莱猜想的奖项颁给格里高利·佩雷尔曼博士"（新闻稿）. 克莱数学研究所. 2010 年 3 月 18 日. 原文存档于 2010 年 3 月 22 日（PDF）。2015 年 11 月 13 日检索. 克莱数学研究所（CMI）今天宣布，来自俄罗斯圣彼得堡的格里高利·佩雷尔曼博士因解决庞加莱猜想而获得千年奖。
7. "Последнее 'нет' доктора Перельмана" [佩雷尔曼博士的最后一个 “拒绝”]. 《国际文传电讯社》（俄语）。2010 年 7 月 1 日。2016 年 4 月 5 日检索。谷歌翻译的存档链接见[1]（存档于 2014 年 4 月 20 日）。
8. Ritter, Malcolm (2010 年 7 月 1 日). "俄罗斯数学家拒绝百万奖金". 《波士顿环球报》。
9. Riemann, Bernhard (1851). 《关于复变函数的一般理论基础》（论文）。哥廷根大学。英文翻译：Riemann, Bernhard (2004). "Foundations for a general theory of functions of a complex variable". 《Collected Papers: Bernhard Riemann》. 翻译者：Baker, Roger; Christenson, Charles; Orde, Henry. Heber City, UT: Kendrick Press. 第 1–41 页. ISBN 0-9740427-2-2. MR 2121437. Zbl 1101.01013.
10. Betti, Enrico (1870). "关于任意维数空间". 《纯数学与应用数学年刊》. 第 4 期: 140–158. doi:10.1007/BF02420029. JFM 03.0301.01.
11. Poincaré, H. (1892). "关于位置分析". 《科学院会议记录》. JFM 24.0506.02.
12. Poincaré, H. (1895). "位置分析". 《高等工科学校学报》. 第 2 系列，第 1 卷：1–121. JFM 26.0541.07.
13. Poincaré, Henri (2010). 《拓扑学论文：位置分析及其五个补充》. 《数学史》. 第 37 卷. 由 John Stillwell 翻译. 美国数学学会与伦敦数学学会. doi:10.1090/hmath/037. ISBN 978-0-8218-5234-7. MR 2723194. Zbl 1204.55002.
14. Gray, Jeremy (2013). 《亨利·庞加莱：科学传记》. 新泽西州普林斯顿：普林斯顿大学出版社. ISBN 978-0-691-15271-4. JSTOR j.ctt1r2fwt. MR 2986502. Zbl 1263.01002.
15. Poincaré, H. (1900). "位置分析的第二个补充". 《伦敦数学学会会刊》. 第 32 卷，第 1 期：277–308. doi:10.1112/plms/s1-32.1.277. JFM 31.0477.10. MR 1576227.
16. 参见 Stillwell 在 Poincaré（2010）中的评论。
17. Poincaré, H. (1904). "位置分析的第五个补充". 《巴勒莫数学会刊》. 第 18 期：45–110. doi:10.1007/bf03014091. JFM 35.0504.13.
18. Poincaré（1904）的开头部分提到 “在词义上真正单连通” 的条件，即与球体同胚的条件。
19. Dieudonné, Jean (1989). 《代数与微分拓扑学史，1900–1960》. 马萨诸塞州波士顿：Birkhäuser Boston, Inc. doi:10.1007/978-0-8176-4907-4. ISBN 0-8176-3388-X. MR 0995842. Zbl 0673.55002.
20. Bing, R. H. (1958). "使三维流形成为 S3 的必要且充分条件". 《数学年刊》. 第二系列. 第 68 卷，第 1 期：17–37. doi:10.2307/1970041. JSTOR 1970041.
21. Bing, R. H. (1964). "与庞加莱猜想相关的三维流形拓扑学的若干方面". 《现代数学讲座》. 第 II 卷. 纽约：Wiley. 第 93–128 页.
22. Halverson, Denise M.; Dušan, Repovš (2008 年 12 月 23 日). "Bing-Borsuk 猜想与 Busemann 猜想". 《数学通讯》. 第 13 卷，第 2 期. arXiv:0811.0886.
23. Milnor, John (2004). "庞加莱猜想 99 年后的进展：进度报告"（PDF）。2007 年 5 月 5 日检索.
24. Taubes, Gary (1987 年 7 月). "当傲慢遇到天命时会发生什么". 《发现》. 第 8 期：66–77.
25. Matthews, Robert (2002 年 4 月 9 日). "$100 万美元数学谜题'解决'". NewScientist.com. 2007 年 5 月 5 日检索.
26. Szpiro, George (2008). 《庞加莱的奖项：解决数学最大难题的百年追寻》. Plume. ISBN 978-0-452-28964-2.
27. Morgan, John W., "庞加莱猜想与三维流形分类的近期进展". 《美国数学学会公报》 (N.S.) 第 42 卷（2005 年），第 1 期，57–78 页.
28. Hamilton, Richard (1982). "具有正 Ricci 曲率的三维流形". 《微分几何学杂志》. 第 17 卷，第 2 期：255–306. doi:10.4310/jdg/1214436922. MR 0664497. Zbl 0504.53034. 重印于：Cao, H. D.; Chow, B.; Chu, S. C.; Yau, S.-T., 编（2003 年）。《Ricci 流的文集》. 《几何与拓扑系列》. 第 37 卷. 马萨诸塞州索美维尔：International Press. 第 119–162 页. ISBN 1-57146-110-8.
29. Perelman, Grigori (2002). "Ricci 流的熵公式及其几何应用". arXiv:math.DG/0211159.
30. Perelman, Grigori (2003). "三维流形上的 Ricci 流与手术". arXiv:math.DG/0303109.
31. Perelman, Grigori (2003). "某些三维流形上 Ricci 流解的有限消失时间". arXiv:math.DG/0307245.
32. Kleiner, Bruce; John W. Lott (2008). "佩雷尔曼论文笔记". 《几何与拓扑》. 第 12 卷，第 5 期：2587–2855. arXiv:math.DG/0605667. doi:10.2140/gt.2008.12.2587. S2CID 119133773.
33. Cao, Huai-Dong; Xi-Ping Zhu (2006 年 6 月). "庞加莱与几何化猜想的完整证明——汉密尔顿-佩雷尔曼 Ricci 流理论的应用"（PDF）。《亚洲数学杂志》。第 10 卷，第 2 期. 原文存档于 2012 年 5 月 14 日（PDF）。
34. Cao, Huai-Dong & Zhu, Xi-Ping (2006 年 12 月 3 日). "汉密尔顿–佩雷尔曼证明庞加莱猜想与几何化猜想". arXiv:math.DG/0612069.
35. Morgan, John; Gang Tian (2006). "Ricci 流与庞加莱猜想". arXiv:math.DG/0607607.
36. Morgan, John; Gang Tian (2007). 《Ricci 流与庞加莱猜想》. 克莱数学研究所. ISBN 978-0-8218-4328-4.
37. Morgan, John; Tian, Gang (2015). "《Ricci 流与庞加莱猜想》第 19.2 节的更正". arXiv:1512.00699 [math.DG].
38. Nasar, Sylvia; David Gruber (2006 年 8 月 28 日). "流形的命运". 《纽约客》. 第 44–57 页. 在线版本见《纽约客》网站.
39. Chang, Kenneth (2006 年 8 月 22 日). "数学最高荣誉被拒绝". 《纽约时报》.
40. 《庞加莱猜想报告》. 约翰·摩根特别讲座.
41. "解答庞加莱猜想的奖项颁给格里高利·佩雷尔曼博士". 克莱数学研究所. 2010 年 3 月 18 日. 原文存档于 2010 年 3 月 22 日.
42. "庞加莱猜想". 克莱数学研究所. 2018 年 10 月 4 日检索.
43. Malcolm Ritter (2010 年 7 月 1 日). "俄罗斯数学家拒绝 100 万美元奖金". Phys.Org. 2011 年 5 月 15 日检索.
44. O'Shea, Donal (2018). "庞加莱猜想的惊人解决". 《庞加莱猜想的惊人解决》. 载于：Rowe, D., Sauer, T., Walter, S.（编）《超越爱因斯坦》. 爱因斯坦研究. 第 14 卷. 纽约：Birkhäuser. 第 401–415 页. doi:10.1007/978-1-4939-7708-6_13. ISBN 978-1-4939-7708-6.

7. 进一步阅读

• Kleiner, Bruce; Lott, John (2008). "佩雷尔曼论文笔记". 《几何与拓扑》. 第 12 卷，第 5 期：2587–2855. arXiv:math/0605667. doi:10.2140/gt.2008.12.2587. MR 2460872. S2CID 119133773.
• Huai-Dong Cao; Xi-Ping Zhu (2006 年 12 月 3 日). "汉密尔顿-佩雷尔曼证明庞加莱猜想与几何化猜想". arXiv:math.DG/0612069.
• Morgan, John W.; Tian, Gang (2007). 《Ricci 流与庞加莱猜想》. 《克莱数学专著》. 第 3 卷. 罗德岛普罗维登斯：美国数学学会. arXiv:math/0607607. ISBN 978-0-8218-4328-4. MR 2334563.
• O'Shea, Donal (2007). 《庞加莱猜想：寻找宇宙的形状》. Walker & Company. ISBN 978-0-8027-1654-5.
• Perelman, Grisha (2002 年 11 月 11 日). "Ricci 流的熵公式及其几何应用". arXiv:math.DG/0211159.
• Perelman, Grisha (2003 年 3 月 10 日). "三维流形上的 Ricci 流与手术". arXiv:math.DG/0303109.
• Perelman, Grisha (2003 年 7 月 17 日). "某些三维流形上 Ricci 流解的有限消失时间". arXiv:math.DG/0307245.
• Szpiro, George (2008). 《庞加莱的奖项：解决数学最大难题的百年追寻》. Plume. ISBN 978-0-452-28964-2.
• Stillwell, John (2012). "庞加莱与三维流形的早期历史". 《美国数学学会通报》. 第 49 卷，第 4 期：555–576. doi:10.1090/S0273-0979-2012-01385-X. MR 2958930.
• Yau, Shing-Tung; Nadis, Steve (2019). 《生命的形状：一位数学家寻找宇宙隐藏的几何》. 康涅狄格州纽黑文：耶鲁大学出版社. ISBN 978-0-300-23590-6. MR 3930611.

8. 外部链接

• 《庞加莱猜想》 – BBC Radio 4 节目《In Our Time》，2006 年 11 月 2 日。参与者：June Barrow-Green，开放大学数学史讲师；Ian Stewart，华威大学数学教授；Marcus du Sautoy，牛津大学数学教授；主持人 Melvyn Bragg。