欧多克索斯（综述）

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科 相关文章。

　　 欧多克斯（Eudoxus of Cnidus，/ˈjuːdəksəs/；古希腊语：Εὔδοξος ὁ Κνίδιος，Eúdoxos ho Knídios；约公元前 390 年—约公元前 340 年）是一位古希腊的天文学家、数学家、医生和立法者。\(^\text{[1]}\) 他是阿尔喀塔斯和柏拉图的学生。他的原始著作均已佚失，但有些片段保存在希帕克斯的《阿拉托斯与欧多克斯〈天象〉注释》中。\(^\text{[2]}\) 比提尼亚的西奥多修斯所著的《球面论》可能是基于欧多克斯的某部著作。

1. 生平

　　 欧多克斯是埃斯喀涅斯之子，出生并去世于克尼多斯（Cnidus，又作 Knidos），这是位于安纳托利亚西南海岸的一座城市。\(^\text{[3]}\) 欧多克斯的出生与去世年份并不确切，但第欧根尼·拉尔修记载了一些传记细节，并提到阿波罗多洛斯说他在第 103 届奥林匹亚会期（公元前 368 年至前 365 年）达到了事业巅峰，并声称他在 53 岁时去世。19 世纪的数学史学家据此推断其生卒年为公元前 408 年至前 355 年，\(^\text{[4]}\) 但 20 世纪的学者认为这些日期相互矛盾，更倾向于其出生于约公元前 390 年。\(^\text{[5]}\)“欧多克斯” 这个名字意为 “受尊敬的” 或 “声誉良好的”（希腊语：εὔδοξος，源自 eu “好” 与 doxa “意见、信念、名声”，相当于拉丁语中的 Benedictus）。

　　 据第欧根尼·拉尔修援引卡利马科斯的《书目》所述，欧多克斯曾在大希腊地区塔兰图姆的阿尔喀塔斯门下学习数学，并向西西里人腓利斯顿学习医学。23 岁时，他与医生忒俄墨冬一同前往雅典学习哲学，忒俄墨冬是他的资助者，也可能是他的情人。\(^\text{[6]}\) 在雅典他只停留了两个月，住在比雷埃夫斯，每天往返七英里（约 11 公里）步行去听智者们的讲座。之后他返回克尼多斯。朋友们后来集资送他前往埃及赫利奥波利斯，在那里他学习了 16 个月的天文学与数学。自埃及北上，他又前往马尔马拉海南岸的基齐库斯，即古称的普罗庞提斯地区。随后他南下前往摩索拉斯之宫廷。在旅途中，他也收了一批自己的学生。

　　 大约在公元前 368 年，欧多克斯带着他的学生返回雅典。有些资料称，在约公元前 367 年柏拉图前往叙拉古期间，他曾担任柏拉图学园的学监，并曾教授过亚里士多德。他最终回到故乡克尼多斯，在城邦议会任职。在克尼多斯期间，他建造了一个天文观测所，并继续撰写著作，讲授神学、天文学和气象学。他育有一子，名为阿里斯塔戈拉斯，另有三位女儿，分别名为阿克提斯、菲尔提斯和德尔菲斯。

　　 在数学天文学方面，欧多克斯因提出同心球体理论而闻名，这一理论是对行星运动的早期解释之一。诗人阿拉托斯也称赞他曾制造过一个天球仪。\(^\text{[7]}\)

　　 他在比例理论上的工作展现出对无理数和线性连续统的洞察：该理论能严谨地处理连续量，而不仅仅局限于整数或有理数。当 16 世纪塔塔利亚等人重新发现这一理论时，它成为自然科学中定量研究的基础，并启发了理查德·戴德金对实数理论的研究。\(^\text{[8]}\)

　　 火星和月球上都有以他命名的陨石坑。此外，一条代数曲线——欧多克斯双曲线也以他命名。

2. 数学

　　 欧多克斯被一些人视为古典希腊最伟大的数学家，整个古代时期仅次于阿基米德。\(^\text{[9]}\) 他很可能是欧几里得《几何原本》第五卷的大部分内容的主要来源。\(^\text{[10]}\) 欧多克斯严谨地发展了安提丰的 “穷竭法”——这是积分学的前身，在后一个世纪中也被阿基米德巧妙地加以运用。在应用这一方法时，欧多克斯证明了一些重要的数学命题，例如：圆的面积之比等于其半径的平方之比，球的体积之比等于其半径的立方之比，锥体的体积等于与其底面积和高相同的柱体体积的三分之一，而金字塔的体积也是相应棱柱体体积的三分之一。\(^\text{[11]}\)

　　 欧多克斯引入了 “未量化的数学量” 这一概念，用以描述并操作诸如线段、角度、面积和体积等连续的几何实体，从而避免了对无理数的直接使用。在此过程中，他逆转了毕达哥拉斯学派对 “数” 与 “算术” 的强调，转而以几何概念作为严谨数学的基础。毕达哥拉斯学派的一些成员，例如欧多克斯的老师阿尔喀塔斯，曾认为只有算术才能为数学证明提供基础。出于对不可通约量（即无法用整数比例表示的量）进行理解与运算的需要，欧多克斯建立了可能是历史上第一个基于显式公理体系的数学演绎结构。欧多克斯的这一思想转向，引发了数学领域长达两千年的分裂。结合当时希腊知识界普遍对实际应用问题缺乏兴趣的态度，也导致了对算术和代数技术发展的显著退却。\(^\text{[11]}\)

　　 毕达哥拉斯学派发现，正方形的对角线与其边长之间不存在共同的度量单位；这就是著名的发现——√2 无法表示为两个整数之比。这个发现预示着在整数和有理分数之外，还存在不可通约的量，但同时也动摇了几何中 “度量” 和 “计算” 这一整体理念的根基。例如，欧几里得在《几何原本》第一卷第 47 命题中（即毕达哥拉斯定理），采用了面积相加的方法给出了一个复杂的证明，而直到第六卷第 31 命题，他才使用相似三角形的方式给出一个更简明的证明，这后一种方法依赖于线段比值的概念。

　　 古希腊数学家并不像我们今天那样使用数值和代数方程来进行计算；他们是通过 “比例关系” 来表达几何量之间的联系。在他们的观念中，两个量的 “比” 并不是一个数值，而是这两个量之间的一种原始关系。

　　 欧多克斯被认为确立了 “两个比相等” 的定义，这正是欧几里得《几何原本》第五卷的核心内容。

　　 在欧几里得《几何原本》第五卷的定义 5 中写道：

　　 “当第一与第二之比与第三与第四之比满足如下条件时，这四个量被称为成同一比例关系：若任意取第一与第三的任意倍数，第二与第四的任意倍数，则在相同的对应顺序下，前者倍数大于、等于或小于后者倍数时，所取的另一组倍数也分别同样大于、等于或小于。”

　　 用现代符号表达，可以更清晰地阐明这一定义。设有四个量 $a, b, c, d$，分别考虑前两个量之比 $a/b$ 与后两个量之比 $c/d$。要说这两个比值相等，即：$a/b = c/d$ 这可以通过如下条件来定义：

　　 对于任意两个正整数 $m$ 和 $n$，分别构造前组的等倍数 $m \cdot a$ 和 $n \cdot b$，以及后组的等倍数 $m \cdot c$ 和 $n \cdot d$。若满足：若 $m \cdot a > n \cdot b$，则必有 $m \cdot c > n \cdot d$；若 $m \cdot a = n \cdot b$，则必有 $m \cdot c = n \cdot d$；若 $m \cdot a < n \cdot b$，则必有 $m \cdot c < n \cdot d$。则称 $a/b = c/d$。这个定义是欧多克斯为了解决无理量与比值问题而建立的严谨比例理论基础，允许在不使用具体数值的前提下，对几何量之间的比例进行逻辑推理。

　　 这意味着，当且仅当那些大于 $a/b$ 的比值 $n/m$ 与那些大于 $c/d$ 的比值完全一致，并且对于 “等于” 和 “小于” 的情况也同样一致时，才可以说：$a/b = c/d$

　　 这种理解方式可以与戴德金分割相比较：戴德金通过某个实数两侧的有理数集合（大于它、等于它、小于它）来定义一个实数。

　　 欧多克斯的定义依赖于对以下类似量的比较：$m \cdot a$ 与 $n \cdot b$,$m \cdot c$ 与 $n \cdot d$ 而不依赖于这些量是否可以用某个共同的单位来度量。

　　 这一定义的复杂性，反映出其中深刻的概念性与方法论上的革新。欧多克斯的比例定义使用了 “对于所有……” 这样的全称量词，从而在逻辑上掌握了 “无限” 和 “无穷小” 的概念，这一点与现代极限和连续性的ε-δ定义极为相似。

　　 而《几何原本》第五卷的定义 4，即阿基米德性质，则是由阿基米德归功于欧多克斯的发明。\(^\text{[12]}\)

3. 天文学

　　 在古希腊，天文学是数学的一个分支；天文学家的目标是建立几何模型，以模拟天体运动的表观现象。因此，将欧多克斯的天文学工作划分为一个独立的领域，其实是一种现代的分类便利。

　　 一些欧多克斯的天文学著作名称虽已流传下来，但原文大多已佚失，这些著作包括：

• 《太阳的消失》：可能是关于日食的讨论；
• 《八年周期》：关于一个由月亮、太阳与金星构成的历法八年周期；
• 《天象》与《镜象》：关于球面天文学，可能基于他在埃及和克尼多斯的观测；
• 《论速度》：关于行星运动的著作。

　　 我们对《天象》的内容相对了解较多，因为欧多克斯的这部散文体著作成为后人阿拉托斯同名诗作的基础。天文学家希帕克斯在其对阿拉托斯诗的注释中曾引用过欧多克斯的原文。

欧多克斯的行星模型

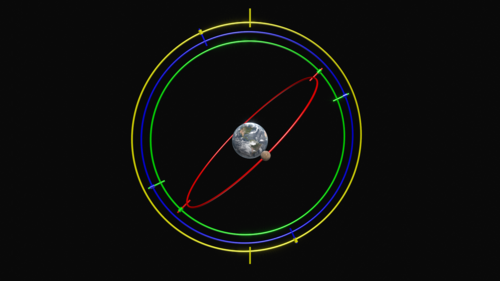
　　 我们可以通过亚里士多德的《形而上学》第十二卷第 8 章，以及 6 世纪的奇里乞亚哲学家辛普利修斯对亚里士多德另一部著作《论天》的注释，对欧多克斯《论速度》一书的内容有一个大致了解。根据辛普利修斯所记载的一个故事，柏拉图曾向希腊天文学家提出一个问题：“通过假设哪些匀速且有序的运动，可以解释行星的表观运动？”\(^\text{[13]}\) 柏拉图设想，那些看似混乱游移的行星运动，其实可以通过围绕球形地球的多个匀速圆周运动的组合来解释——这一设想在公元前 4 世纪似乎还是一个新颖的思想。

　　 在多数现代对欧多克斯模型的重建中，月球被分配了三个球体：

• 最外层的球体以 24 小时为周期向西转动，用以解释月亮的东升西落；
• 第二层的球体以一个月为周期向东转动，用以解释月亮在黄道带中的月度移动；
• 第三层的球体同样以一个月为周期完成旋转，但其轴线略有倾斜，用以解释月亮在纬度方向上的偏移（即偏离黄道的运动）以及交点的移动。

　　 太阳也被分配了三个球体：

　　 其中第二层球体的运动周期是一年而非一个月；第三层球体的存在说明欧多克斯误以为太阳也存在纬度方向上的运动（即认为太阳也会偏离黄道），这一点被认为是他的一处错误认知。

　　 五大可见行星（即水星、金星、火星、木星和土星）每颗都被分配了四个球体：

• 最外层球体用来解释其每日的升落运动；
• 第二层球体用来解释行星在黄道带中的正常运行；
• 第三层与第四层球体共同用来解释逆行现象，即行星在黄道中似乎先减速、然后短暂地反向运动的现象。 通过使这两个球体的轴线彼此倾斜，并以相反的方向、但相同的周期旋转，欧多克斯能够使内层球体上的某一点描绘出一个 “8” 字形轨迹，即所谓的马镫形曲线。

欧多克斯体系的重要性

　　 公元前 4 世纪的希腊天文学家卡利波斯在欧多克斯原有的 27 个球体基础上又增加了 7 个球体（除了行星的球体外，欧多克斯还包括了一个用于恒星的球体）。亚里士多德描述了这两种体系，但他坚持在每组球体之间增加 “抵消球”，以抵消外层球体的运动对内层球体的影响。亚里士多德关心的是该体系的物理本质；如果没有 “抵消球”，外层的运动就会被传递到内层行星上。

　　 欧多克斯体系的一个重大缺陷在于，它无法解释行星亮度的变化，即从地球上观察，行星有时更亮、有时更暗。由于这些球体是同心的，行星距离地球的距离始终保持不变，因此无法解释亮度的变化。这一问题在古代就已被皮塔尼的奥托吕科斯指出。

　　 后来，天文学家通过引入本轮与均轮体系来解决这个问题，这使得行星与地球之间的距离可以变化。然而，尽管存在这些局限，欧多克斯在天文学，尤其是在希腊天文学中的重要地位，依然不可动摇。

4. 伦理学

　　 亚里士多德在《尼各马科伦理学》中[14]将一项支持享乐主义（即认为 “快感是人类行为所追求的最高善”）的主张归于欧多克斯。据亚里士多德所述，欧多克斯为这一观点提出了如下论证：

1. 所有事物——无论有理还是无理的——都追求快感；而一切事物都趋向于它们所认为的 “善”；因此，若要判断什么是 “至善”，一个有力的指示就是看什么是最多事物所共同追求的目标。
2. 类似地，快感的对立面——痛苦——被普遍地避开，这进一步支持了 “快感被普遍视为善” 的观点。
3. 人们追求快感，并非为了获得其他目的，而是作为自身目的去追求快感；这说明快感是终极目的。
4. 任何你能想到的善，如果加入快感都会变得更好；而只有 “善” 才能使 “善” 更加完善。
5. 在所有被称为 “善” 的事物中，唯有 “幸福” 不被人称颂（即人们不会说 “幸福是好的”——因为它本身就是 “善” 的顶点），这或许说明幸福才是至高的善。[15]

5. 参见

• 欧多克斯实数：一种较为近代发现的实数构造方式，以他命名；
• 德利安问题：古希腊数学的经典难题；
• 不可通约量；
• 斯培乌西波斯：柏拉图的侄子、学院的继承人，与欧多克斯思想有所交集。

6. 参考文献

1. 第欧根尼·拉尔修，第八卷第 86 节
2. Lasserre, François（1966），《欧多克斯残篇》，柏林：德古意特出版社
3. O'Connor, John J.; Robertson, Edmund F.，“Cnidus 的欧多克斯”，圣安德鲁斯大学 MacTutor 数学史档案馆
4. Hultsch, 1907
5. De Santillana, George（1940），“欧多克斯与柏拉图：一项时间学研究”，Isis，第 32 卷第 2 期，第 248–262 页，doi:10.1086/347693，JSTOR: 226242
6. 第欧根尼·拉尔修，第八卷第 87 节
7. Sumira, Sylvia（2014），《地球仪简史》，载于《地球仪：探索、航行与权力的四百年》，芝加哥大学出版社，第 13 页，doi:10.7208/9780226139142-005（2024 年 11 月 1 日失效），ISBN 9780226139142
8. Nikolić, Milenko（1974），“欧多克斯比例理论与戴德金分割理论的关系”，载于 Cohen, Robert S.; Stachel, John J.; Wartofsky, Marx W. 编，《献给 Dirk Struik 的科学、历史与政治论文集》，波士顿科学哲学研究，第 15 卷，Dordrecht: Springer，第 225–243 页，doi:10.1007/978-94-010-2115-9_19，ISBN 978-90-277-0379-8
9. Calinger, Ronald（1982），《数学经典》，伊利诺伊州奥克帕克：Moore Publishing Company，第 75 页，ISBN 0-935610-13-8
10. Ball, 1908，第 54 页
11. Kline, Morris，《从古代到现代的数学思想》，牛津大学出版社，1972 年，第 48–50 页
12. Knopp, Konrad（1951），《无穷级数的理论与应用》（英文第二版），伦敦与格拉斯哥：Blackie & Son 出版社，第 7 页
13. Lloyd, G.E.R.（1970），《早期希腊科学：从泰勒斯到亚里士多德》，W\.W. Norton 出版社，第 84 页，ISBN 9780393005837
14. （欧几里得）《几何原本》第十卷中大量涉及
15. 上述享乐主义论证见于《伦理学》第一卷

7. 参考书目

• Ball, Walter William Rouse（1908），《数学史简述》（第 4 版），多佛出版社，ISBN 9780486206301
• Evans, James（1998），《古代天文学的历史与实践》，牛津大学出版社，ISBN 0-19-509539-1，OCLC 185509676
• Hultsch, Friedrich（1907），“欧多克斯·冯·克尼多斯”，载于 Pauly, August 与 Wissowa, Georg 编，《古典古代百科全书》（Realencyclopädie der classischen Altertumswissenschaft，德文），第 6.1 卷，第 930–950 页，通过维基文库访问
• Huxley, G. L.（1980），《克尼多斯的欧多克斯》，收录于《科学传记词典》第 4 卷，第 465–467 页
• Huxley, G. L.（1963），《欧多克斯专题》，*希腊、罗马与拜占庭研究*，第 4 期，第 83–96 页
• Knorr, Wilbur Richard（1978），《阿基米德与欧几里得之前的比例理论》，*国际科学史档案*，第 28 卷，第 183–244 页
• Knorr, Wilbur R.（1986），《几何问题的古典传统》，波士顿：Birkhäuser 出版社，ISBN 0-8176-3148-8
• Lasserre, François（1966），《克尼多斯的欧多克斯残篇》，柏林：德古意特出版社
• 第欧根尼·拉尔修，《哲人言行录·毕达哥拉斯学派：欧多克斯》，第 2 卷第 8 章，R.D. Hicks 英译，Loeb 古典文库双卷本
• Manitius, C.（1894），《希帕克斯评注阿拉托斯与欧多克斯〈天象〉三书》（Teubner 出版社）
• Neugebauer, O.（1975），《古代数学天文学史》，柏林：施普林格出版社，ISBN 0-387-06995-X
• Van der Waerden, B. L.（1988），《科学的觉醒》（第 5 版），莱顿：Noordhoff 出版社

8. 外部链接

• 《欧多克斯与柏拉图》纪录片，介绍欧多克斯及其行星模型（2018 年 8 月 16 日存档）
• Dennis Duke，“欧多克斯〈天象〉的统计年代考证”，载《DIO》第 15 卷，第 7–23 页
• 克尼多斯的欧多克斯
• “克尼多斯的欧多克斯”，德克萨斯农工大学 Donald Allen 教授撰写（1997 年 7 月 23 日存档）
• “克尼多斯的欧多克斯：天文学与同心球体”，Henry Mendell，加州州立大学洛杉矶分校（2011 年 5 月 16 日存档）
• 赫罗多德计划：克尼多斯黑白摄影文献集
• “行星运动模型——欧多克斯”，Craig McConnell 博士，加州州立大学富尔顿分校（2011 年 7 月 19 日存档）
• “欧多克斯眼中的宇宙”（Java 小程序）（2007 年 11 月 21 日存档）