数值解常微分方程（入门）

贡献者： addis

　　¹前面几节，我们把求解线性方程组的基本数值方法做了详细的介绍和分析。从这一节开始，我们来尝试使用这些解法，处理更复杂也更贴近实际应用的问题。需要复习小伙伴，可以先去看看前面的内容。

　　 这一节我们来讨论一下常微分方程（Ordinary Differential Equation（ODE））。注意，我的整个专栏都是在讨论关于科学计算和数值分析的内容。对于常微分方程的分析特性，解析特解和通解等特性，请参考数学分析课程等。

举个例子

　　 比如，$y'(t)= \cos\left(yt\right) $，这实际上是一个非线性的常微分方程，而且 $y$ 还隐含的是 $t$ 的函数。

　　 再比如，$y'(t)=ay(t)+b$，如果 $a$ 和 $b$ 都是常数的话，这就是一个线性常微分方程。

　　 再再比如，$y'(t)=at+b$，求解这个方程可以轻松的将右边对 $t$ 做积分。

　　 当然，我们也可以写出常微分方程的标准形式

　　 那么，对于上面这样的一个微分方程，我们可以从两个不同的角度来得到几乎相同的数值方法。一种是将左边的导数进行泰勒展开的近似，另一种则是将整个方程积分。

1. 数值方法——泰勒展开观点

　　 我们考虑一个很小的值 $h$

1. 对 $y(t+h)$ 做泰勒展开可以得到 $y(t+h)=y(t)+hy'(t)+\frac{h^2}{2!}y''(t)+\cdots$。我们舍去高次项，仅保留一阶导数，则 $y'(t)\approx \frac{y(t+h)-y(t)}{h}= f(y(t),t)$。这样就得到了Forward Euler方法，它的离散化误差（Discretization error）是 $e=\mathcal{O}(h)$。很显然，这个更新过程这是一个显式方法（Explicit method）。
2. 同样的，对 $y(t)$ 做泰勒展开还可以得到 $y(t)=y(t+h)-hy'(t+h)+\frac{h^2}{2!}y''(t+h)-\cdots$。我们同样只保留一阶导数，就得到了 $y'(t+h)\approx \frac{y(t+h)-y(t)}{h}= f(y(t+h),t+h)$。这就是Backward Euler方法，它的离散化误差（Discretization error）同样是 $e=\mathcal{O}(h)$。但是，由于 $y(t+h)$ 同时出现在等式左右两端，因此需要求解这个方程，才能得到 $y(t+h)$ 的值，因此这是一个隐式方法（Implicit method）。
3. 我们用 1）和 2）方法的平均值，就得到了一个新的方法：$ \frac{y(t+h)-y(t)}{h}= \frac{1}{2}\left(f(y(t+h),t+h)+f(y(t),t)\right)$。这个方法事实上就是所谓的梯形公式（Trapezoidal rule）。它仍然是一个隐式方法，但他的离散化误差提高到了是 $e=\mathcal{O}(h^2)$。有兴趣的小伙伴可以自己用泰勒展开验证一下。

2. 数值方法——数值积分观点

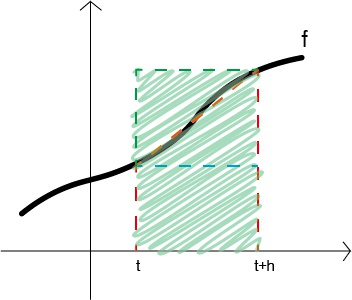
　　 上面所述的三种方法也可以从数值积分中推导出，我们先将微分方程两边同时积分，得到 $y(t+h)=y(t)+\int_t^{t+h}f \rm{d}s$。这个积分的值简单理解就是如下图所示，求函数 $f$ 与横坐标轴在 $t$ 到 $t+h$ 之间围成的面积。它们的数值方法有很多形式，例如

1. 我们可以用下面蓝色的长方形区域来近似这个面积
   
   图 1：用长方形近似面积
   $y(t+h)\approx y(t)+hf(y(t),t)$。这正好就是 Forward Euler 方法。
2. 我们也可以用下面的绿色区域来近似这个面积
   
   图 2：用长方形近似面积
   $y(t+h)\approx y(t)+hf(y(t+h),t+h)$。这就是Backward Euler方法。
3. 还可以用下面的橙色梯形区域来近似
   
   图 3：用梯形近似面积
   $y(t+h)\approx y(t)+\frac{1}{2}h\left(f(y(t),t)+f(y(t+h),t+h)\right)$。这正好就Trapezoidal rule，即梯形公式名字的由来。

3. 总结一下

　　 我们把 $y(t_i)$ 称作精确解或者解析解，它的数值近似解记做 $y_i$。

• Forward Euler: $y_{n+1}=y_n+hf(y_n,t_n)~.$
• Backward Euler: $y_{n+1}=y_n+hf(y_{n+1},t_{n+1})~.$
• Trapezoidal Rule: $y_{n+1}=y_n+\frac{h}{2}\left(f(y_n,t_n)+f(y_{n+1},t_{n+1}) \right)~.$

4. 求解步骤

　　 我们来简单概括一下常微分方程的求解过程：

1. 从初始值开始，令 $y_0=y(t_0)=\hat{y}$。
2. 根据所选用的数值方法，计算出 $y_1$。这里的方法可以是 Forward/Backward Euler，也可以是梯形公式，还可以是其他的一些方法。
3. 将第 2 步的操作重复应用到由 $y_i$ 计算 $y_{i+1}$ 的过程。直到 $t_i\ge T$ 时，停止。

需要注意

　　 在上面的第 2 步使用 Backward Euler 或者梯形公式时，由于它们均为隐式方法，每一步都需要求解一个线性或非线性方程。我们考虑简单的常微分方程 $y'=f(y)$，以 Backward Euler 为例，数值方法为 $y_{n+1}=y_{n}+hf(y_{n+1})$ 即 $y_{n+1}-hf(y_{n+1})=y_{n}$

• 若 $f(y)=\lambda y$，则 $y_{n+1}=\frac{1}{(1-h\lambda)}y_n$
• 若 $f(y)=A y$，且 A 为矩阵，f 和 y 为向量时，那么我们需要求解线性方程组 $(I-hA)y_{n+1}=y_n$ 来得到新的 $y_{n+1}$
• 若 $f(y)=y^2$，则 $y_{n+1}-hy^2_{n+1} = y_n$ 这是一个非线性方程，通常需要迭代法求得数值解。

　　 这也就意味着，通常情况下如果采用隐式方法会比显式方法的运算复杂度更高。因此，在没有特殊要求的前提下，我们更偏向于使用显式方法求解常微分方程。（当然，我们会在后面的章节中具体讨论，哪些特殊情况下必须或者更偏向于使用隐式方法）

5. 更多方法

　　 也正是因为上面的原因，Karl Heun 将梯形公式改进成了显式方法----Heun 方法。它的核心思想就是用 Forward Euler 方法求出 $\tilde{y}_{n+1}=y_n+hf(y_n,t_n)$，然后带入到梯形公式的右边，$y_{n+1}=y_n+\frac{h}{2}\left(f(y_n,t_n)+f(\tilde{y}_{n+1},t_{n+1}) \right)$。这样整个过程的每一步都是显式方法，从而避免了任何可能出现的解方程的过程。当然，有些资料上面也会这样描述 Heun 方法：

　　 事实上，这种形式是另一种更有名的方法的二阶特例，即龙格－库塔法（Runge-Kutta）。例如，我们最常见的 RK4 的形式为

　　 当然，关于不同阶数 RK 方法的系数推导以及误差分析，已经超出了这个专题的范围，有兴趣的小伙伴可以留言，我会单独开一个专题来讨论。

最后一个例子

　　 我们来尝试着用上面的一些显式方法来求解一个非线性常微分方程：

　　 我们分别用了 Forward Euler，Heun 和 RK4 方法，其中，Python 的科学计算包 scipy.integrate.solve_ivp 提供了例如 RK45（即我们上面提到的 RK4），BDF（后面我们会专门讨论它）以及其他的一些常用方法。

　　 有兴趣的小伙伴可以尝试着自己调整步长参数和方法，来看看误差的变化。

from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
import numpy as np

def rhsODEs(t, y):
    return y - 0.5*np.exp(0.5*t)*np.sin(5*t)+5*np.exp(0.5*t)*np.cos(5*t)

# initial condition
y0 = [0]
N = 20

# Time steps
t_span = (0, np.pi)
t_eval = np.linspace(t_span[0], t_span[1], 1000)

# Solve for the ODE with R-K method
sol_ex = solve_ivp(rhsODEs, t_span, y0, method='RK45', t_eval=t_eval)
sol_fe = EulerForward(rhsODEs, t_span, y0, N)
sol_he = Heun(rhsODEs, t_span, y0, N)
t_evalRK = np.linspace(t_span[0], t_span[1], N)
sol_rk = solve_ivp(rhsODEs, t_span, y0, method='RK45', t_eval=t_evalRK)

# plot
fig, ax = plt.subplots(1, figsize=(6, 6))
ax.plot(sol_ex.t,sol_ex.y.T )
ax.plot(sol_fe[0], sol_fe[1],'-*' )
ax.plot(sol_he[0], sol_he[1],'-o' )
ax.plot(sol_rk.t,sol_rk.y.T, '-d')

ax.autoscale(enable=True, axis='both', tight=True)
ax.set_ylabel(r'$y(t)$')
ax.set_xlabel(r'$t$')
ax.legend(['Exact solution(RK45)','Forward Euler Method',
    'Heuns Method', 'Classical Runge-Kutta'])

　　 三种方法的结果如图，另外为了作为参照，我们选用了非常小的时间间隔，用 RK45 模拟出了一个解析解。

　　 注：这里我自己写了 Forward Euler（或者叫 Euler Forward）和 Heun 方法如下：

import numpy as np

def EulerForward(func, t_span, y0, n):
    """ Explicit Euler method
    Parameters
    ----------
    func : function, function handler of the right hand side of the ODE(s);
    t_span : list, t_span[0] is the initial time, t_span[1] is the final time;
    y0 : float, list, initial condition(s) of the ODE(s);
    n : number of time steps, dt = (t_span[1]-t_span[0])/n.
        
    Returns
    -------
    t : list, the resulting time steps;
    y : list, the solutions of the ODE(s)
    """
    t = np.linspace(t_span[0], t_span[1], n)
    dt = t[1]-t[0]
    y = [y0]
    for i in range(n-1):
        ynp1 = y[i] + dt*func(t[i], y[i])
        y.append(ynp1)
    return t, y
    
    
def Heun(func, t_span, y0, n):
    """ Heun's method
    Parameters
    ----------
    func : function, function handler of the right hand side of the ODE(s);
    t_span : list, t_span[0] is the initial time, t_span[1] is the final time;
    y0 : float, list, initial condition(s) of the ODE(s);
    n : number of time steps, dt = (t_span[1]-t_span[0])/n.
        
    Returns
    -------
    t : list, the resulting time steps;
    y : list, the solutions of the ODE(s)
    """
    t = np.linspace(t_span[0], t_span[1], n)
    dt = t[1]-t[0]
    y = [y0]
    for i in range(n-1):
        k1 = func(t[i], y[i])
        k2 = func(t[i+1], y[i]+dt*k1)
        ynp1 = y[i] + 0.5*dt*(k1+k2)
        y.append(ynp1)
    return t, y

最后一点

　　 我们在这个例子中可以观察到一点，这三种方法的误差排序大体上是 Forward Euler > Heun > RK4。那么，下一章我们会来具体分析这其中的原因，也就是所谓的局部残差（local truncation error）和全局误差（global error）。

1. ^ 本文经作者同意转载自知乎专栏 《科学计算》，格式有少量修改。