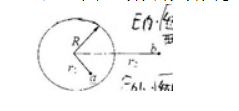南京理工大学 普通物理 B（845）模拟五套卷 第三套

贡献者： 待更新

　　 声明：“该内容来源于网络公开资料，不保证真实性，如有侵权请联系管理员”

1. 一、填空题 I（26 分，每空 2 分）

　　 1. 一质点的运动方程(SI)为：$x=-10t+30t^2,y=15t-20t^2$，则质点的起始速度为__________，质点加速度为____________。

　　 2. 质量为 $m$，长为 $l$ 的匀质细杆，可绕其端点的水平轴在竖直平面内自由转动。如果将细杆置于水平位置，然后让其由静止开始自由下摆，则开始转动的瞬间，细杆的角加速度为_____________，细杆转动到竖直位置时的角速度为_________________。

　　 3. 如图所示，一长为 $l$ 的均匀直棒可绕过其一端且与棒垂直的水平光滑固定轴转动。抬起另一端使棒向上与水平面成 60°，然后无初速地将棒释放。已知棒对轴的转动惯量为 $\frac{1}{3}ml^2$，其中 $m$ 和 $l$ 分别为棒的质量和长度，则放手时棒的角加速度为________，棒转到水平位置时的角加速度为_________________。

　　 4. 已知一平面简谐波频率为 $1000Hz$，波速为 $300m/s$，则波上相差 $\pi/4$ 的两点之间的距离为_______________，在某点处时间间隔为 $0.001s$ 的两个振动状态间的相位差为_________。

　　 5. 一质点作简谐振动，速度最大值 $Vm=5cm/s$，振幅 $A=2cm$，若令速度具有正最大值的那一时刻为 $t=0$，则振动表达式为_____________。

　　 6. 互感系数的物理意义是______________。

　　 7. 在容积为 $10^{-2}m^3$ 的容易中，装有质量为 $100g$ 的气体，若气体分子的方均根速率为 $300mS^{-1}$，则气体的压强为____________。

2.、填空题 II（20 分，每空 2 分）

　　 1. 在棱镜 $(n1=1.52)$ 表面镀一层增透膜 $(n2=1.30)$，如使此增透膜适用于 $550.0nm$ 波长的光，则膜的厚度为____________。

　　 2. 如图所示，半径为 $r_1$ 的小导线环，置于半径为 $r_2$ 的大导线环中心，二者在同一平面内，且 $r_1< r_2$。在大导线环中通过正弦电流 $I=I_0\sin^\omega t$，其中 $\omega ,I_0$ 为常数，$t$ 为时间，则任一时刻小导线环中感应电动势的大小为____________。设小导线环的电阻为 $R$，则在 $t=0$ 到 $t=\pi/(2^\omega )$ 时间内，通过小导线环某截面的感应电量为_______________。

　　 3. 自然光通过两个偏振化方向成 60°的偏振片，透射的光强为 $I_1$，今在这两个偏振片之间加入另一个偏振片，与两个夹角均为 30°，透过的光强为___________。

　　 4. 自感为 $0.25H$ 的线圈中，当电流在 $1/16s$ 内由 $2A$ 均匀减小到零时，线圈中自感电动势的大小为____________。

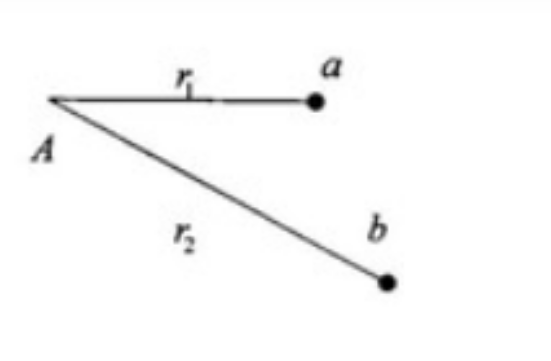
　　 5. 在电荷为 $-Q$ 的点电荷 $A$ 的静电场中，将另一电荷为 $q$ 的点电荷 $B$ 从 $a$ 点移到 $b$ 点，$a,b$ 两点距离点电荷 $A$ 的距离分别为 $r_1$ 和 $r_2$，如图所示，则移动过程中电场力做的功为______________。

　　 6. 一粒子静质量为 $m_0$，其动能是静能的 $n$ 倍，则该粒子的运动质量为_________，运动速度大小为_____________。

　　 7. 处于 $n=4$ 激发态的氢原子，它回到基态的过程中，所发出的光波波长最短为___________$nm$，最长为____________$nm$。

3. 三、（13 分）

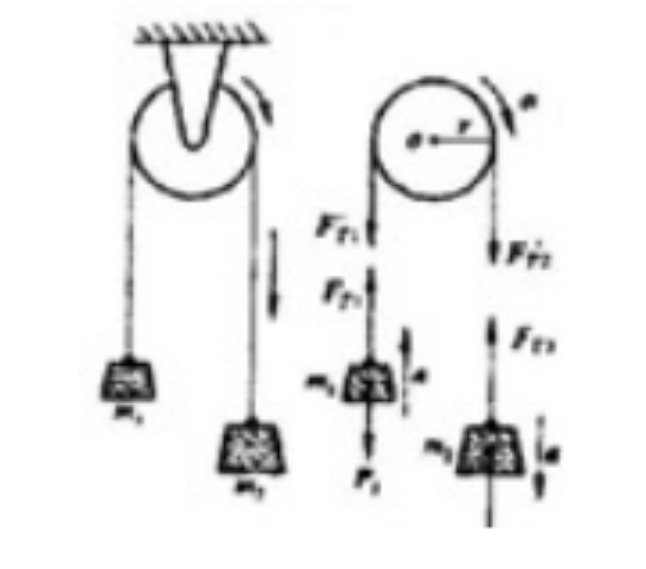
　　 一细轻绳跨过一个半径为 $r$、质量为 $m$ 的定滑轮，滑轮可视为圆盘。绳的两端分别系有质量为 $m_1$ 和 $m_2$ 的物体，$m_1< m_2$，如图所示，设绳子与滑轮之间无相对滑动，试求物体的加速度和绳子的张力。

4. 四、（13 分）

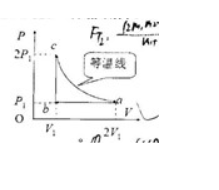
　　 $1mol$ 氦气经历如图所示的循环过程，试求循环效率。

5. 五、（12 分）

　　 一半径为 $R$ 的无限长带电棒，其内部的电荷均匀分布，电荷体密度为 $\rho$。求： （1）电场分布；
（2）如图所示（沿棒轴向俯视），若点电荷 $q_0$ 从 $a$ 点运动到 $b$ 点，则电场力做功为多少？

6. 六、（12 分）

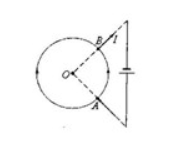
　　 两根长直导线沿半径方向引到均匀铁环上的 $A,B$ 两点，并与很远的电源相连，如图所示，求环中心 $O$ 的磁感应强度。

7. 七、（14 分）

　　 两根平行导线，横截面的半径都是 $a$，中心相距为 $d$，载有大小相等而方向相反的电流。设 $d>a$，且两导线内部的磁通量都可略去不计。求这样一对导线长为 l 段的自感系数 $L$。

8. 八、（14 分）

　　 一轻弹簧的劲度系数为 $k$，其下端悬有一质量为 $M$ 的盘子。现在有一质量为 $m$ 的物体从离盘底为 $h$ 高度处自由下落到盘中并和盘子粘在一起，于是盘子开始振动。若以物体落到盘底时为计时零点，以物体到盘子后的平衡位置为坐标原点，以向下为 x 轴正向，求盘子的振动方程。

9. 九、（13 分）

　　 一光栅，在 $2.4cm$ 宽度上有 6000 条刻痕，其刻痕宽度是透光缝宽的二倍，现以波长 $\lambda=632.8nm$ 的单色平行光垂直照射，求：（1）光栅常数；（2）最多能观察到哪些谱线，共有多少条？

10. 十、（13 分）

　　 已知两质点 $A,B$ 静止质量均为 $m_0$，若质点 $A$ 静止，质点 $B$ 以 $6m_0c^2$ 的动能向 $A$ 运动，碰撞后合成一粒子。若无能量释放，求合成粒子的静止质量和速度。