南京理工大学 2006 年 研究生入学考试试题 普通物理（B）

贡献者： 待更新

　　 声明：“该内容来源于网络公开资料，不保证真实性，如有侵权请联系管理员”

1. 填空题(26 分，每空 2 分)

1. 一质点作平面运动，运动方程为 $\vec{r} = (3t + 1) \hat{i} + (t^2 - 1) \hat{j}$，则 t 时刻质点的速度为 $\underline{\hspace{2cm}}$，加速度为 $\underline{\hspace{2cm}}$。
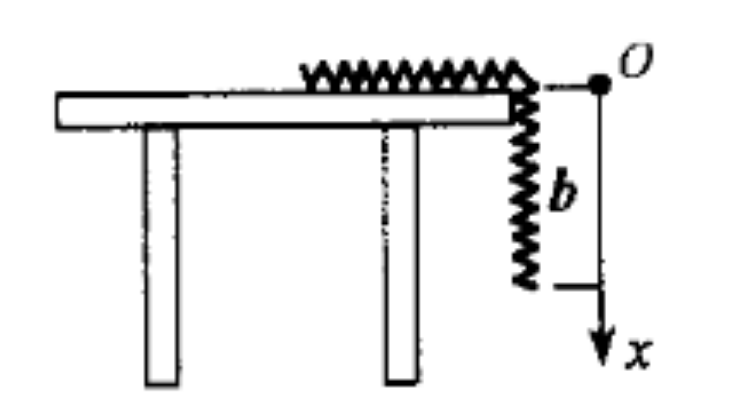
2. 质量 $m$ 均匀分布的链条，总长为 $L$，有长度 b 伸在桌外。若自静止释放，则链条全部脱离光滑桌面的速度为 $\underline{\hspace{3cm}}$，加速度为 $\underline{\hspace{3cm}}$，若以桌面为势能零点，此时的势能为 $\underline{\hspace{3cm}}$。
   
   图 1
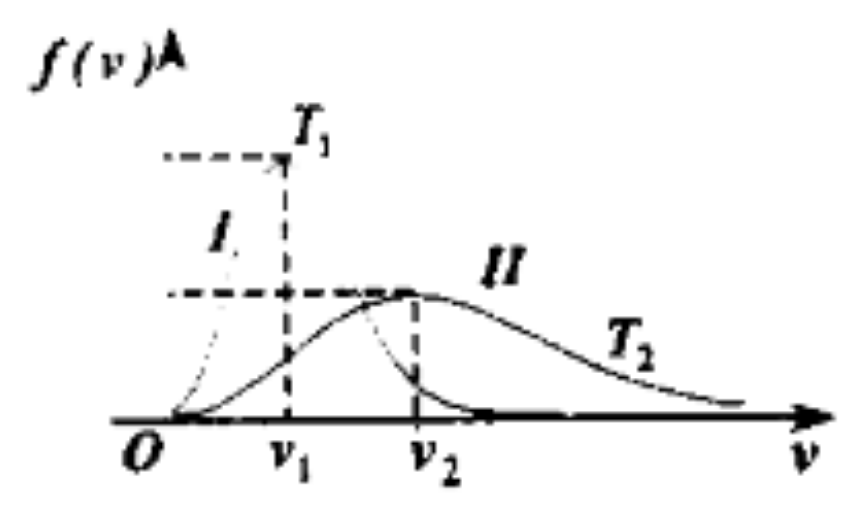
3. 如图，曲线 I 表示 $27^\circ C$ 的氧气分子的 Maxwell 速度分布，则图示中 $v_1 = \underline{\hspace{3cm}}$（6）。设曲线 II 也表示氧气分子某一温度下的 Maxwell 速度分布，且 $v_2 = 600 , m/s$，则曲线 II 对应的理论体温标 $T_2 = \underline{\hspace{3cm}}$。
   
   图 2
4. 一理想卡诺循环一次卡诺循环对外做功 1000J，卡诺循环高温热源温度 $T_1 = 500K$，低温热源温度 $T_2 = 300K$，则在一次循环中，在高温热源处吸热 $Q_1 = \underline{\hspace{3cm}}$，在低温热源处放热 $Q_2 = \underline{\hspace{3cm}}$。
5. 弹簧振子的振动周期为 T，现将弹簧截去一半，则新弹簧质子的振动周期为 $\underline{\hspace{3cm}}$，再将两半弹簧并联使用，则其振动周期变为 $\underline{\hspace{3cm}}$。
6. 一平面简谐波方程（波函数）为 $y_1 = A \cos 2 \pi \left( \frac{t}{T} - \frac{x}{\lambda} \right)$，在 $x = \frac{\lambda}{2}$ 处有一反射壁，若平面波从空气传到反射壁而反射，反射时振幅不变，已知空气为波介质，则反射波波动方程为 $\underline{\hspace{3cm}}$，波节点的位置为 $\underline{\hspace{3cm}}$。

2. 填空题(30 分，每空 2 分)

1. 半径为 $R$，带电量为 $Q$ 的金属导体球，其外表面处的电场强度大小为 $\underline{\hspace{2cm}}$，导体球内部或距球心 $r (< R)$ 处的电势为 $\underline{\hspace{2cm}}$。导体球外距球心 $r$ 处的电势为 $ \underline{\hspace{3cm}}$。
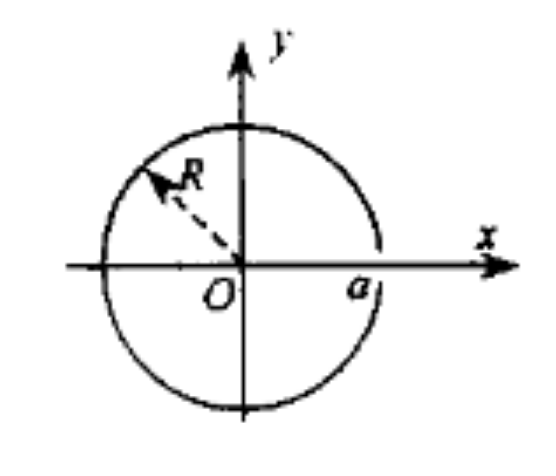
2. 一半径为 $R$ 的无限长薄圆管，平行轴向有一宽度为 $a$ ( $a \\ll R$ ) 的无限长细线，如图所示。管壁上均匀地通有稳恒电流，设管壁圆周上单位长度电流为 $I$，方向垂直纸面向上，则轴 $O$ 处的磁感应强度大小 $B_0 =$ $\underline{\hspace{2cm}}$，方向为 $\underline{\hspace{2cm}}$;
   
   图 3
3. 在两个偏振化方向正交的偏振片之间插入第三个偏振片，当最后透过的光强为入射的自然光强的 $\frac{1}{8}$ 时，第三个偏振片偏振化方向与第一个偏振片偏振化方向的夹角为 $\underline{\hspace{2cm}}$，当最后透射光强为零时，第三个偏振片偏振化方向与第一个偏振片偏振化方向的夹角为 $\underline{\hspace{2cm}}$。
4. 用氢-氖激光器发出的波长为 $632.8\text{nm}$ 的单色光做牛顿环实验，测得第 $k$ 级暗环的半径为 $5.625\text{mm}$，第 $k+5$ 级暗环的半径为 $7.956\text{mm}$，则所用平凸透镜的曲率半径 $R =$ $\underline{\hspace{2cm}}$，$k$ 的级数为 $\underline{\hspace{2cm}}$。
5. 静系中测得一棒的长度为 $l$，其质量线密度为 $p$，若此棒沿其长度方向以速度 $v$ 运动，其线密度为 $\underline{\hspace{2cm}}$，若此棒沿与其长度方向垂直的方向以速度 $v$ 运动，其线密度为 $\underline{\hspace{2cm}}$
6. 基态氢原子中的电子吸收一个能量为 $13.0ey$ 的光子后所能到达的最高能态为 $\underline{\hspace{2cm}}$，从该能态直接跃迁回基态辐射的光子频率为 $\underline{\hspace{2cm}}$
7. 爱因斯坦光电效应方程为 $\underline{\hspace{2cm}}$，某金属的电子逸出功为.4.2 电子伏特，要从金属表面释放出电子，照射光的波长必须满足 $\underline{\hspace{2cm}}$

3. (12 分)

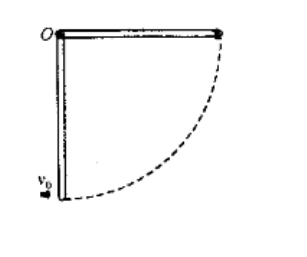
　　 一长为 $L$ 质量为 $m$ 的均细棒，一端可绕水平光滑轴 $O$ 在竖直平面内转动。当细棒静止在竖直位置时，有质量为 $m_0$，速度为 $v_0$ 的子弹，水平射入其下端而不复出。此后棒摆到水平位置后重又下落。求子弹射入棒前的速度 $v_0$”。

4. (10 分)

　　 劲度系数为 $k$ 的轻弹，上端接一水平的轻平台，下端固定于地面。当质量为 $m$ 的人站于平台上，弹簧压缩了 $x_0$，并由此位置开始向下运动作为初始时刻，设系统振动的振幅为 $A$，且向下为正，求振动方程。

5. (12 分)

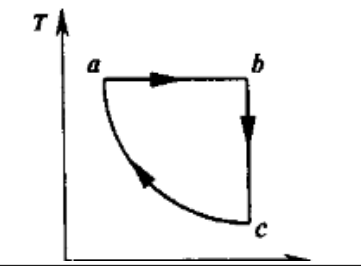
　　 如图为一循环过程的下 $T-V$ 图线。该循环的工质为 $v mol$ 的理想气体，其 $C_r,m$ 和 $r$ 均已知且为常量。已知 $a$ 点的温度为 $T_1$，体积为 $V_1,b$ 点的体积为 $V_2,ca$ 为绝热过程。求循环的效率。

6. (12 分)

　　 长为 $L$ 的圆柱形电容器内外半径分别为 $R_1$,和 $R_2$,，其间充满相对介电常数为 $\varepsilon$,的均匀介质，电容器带电量为 $Q$。求:

　　 (1)两极间的电势差:(2)电容器的电容;(3)系统储存的电场能:

7. (12 分)

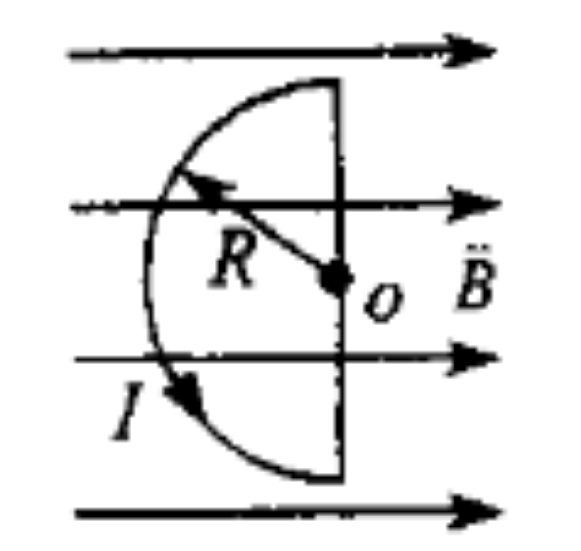
　　 一个半径 $R=0.18m$ 的半圆形闭合线圈，载有电流 $I=10A$，放在 $B-10T$ 的均匀外磁场中，磁场方向与线圈平面平行，如图所示。求:

　　 (1)线圈磁矩的大小与方向;

　　 (2)线圈所受磁力矩的大小与方向;

　　 (3)在磁力矩作用下，线圈平面绕纸面内过 0 点的竖直轴转过 $\pi/2$ 时，磁力矩作的功(设 $I$ 在旋转过程中不变)。

8.（12 分）

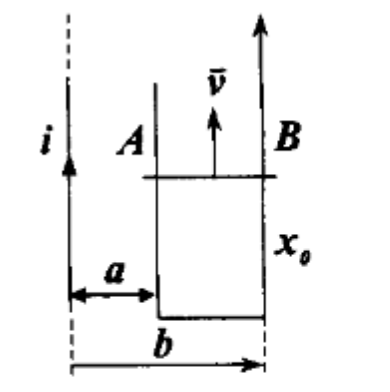
　　 如图所示，在长直导线旁有一与之共面的矩形线框，其中 $AB$ 在线框上以速度 $v$ 沿平行导线方向运动，线框两边与导线平行，距离分别为 $a$ 和 $b,t=0$ 时 $AB$ 边离线框起点为 $x_0$，长直导线中通以变化电流 $I = I_0 \cos{\omega t}$，求线框中的感应电动势。

9.（12 分）

　　 波长 $\lambda = 600 nm$ 的单色光垂直入射在一光栅上，第二级明线出现 在 $\sin{\theta_2} = 0.3$ 处，第四级为第一个缺级。求：① 光栅常数；② 屏上可观察到的明级数及其级数。

10.（12 分）

　　 动能为 $2eV$ 的电子，从无穷远处向着静止的氢原子运动，最后被质子所束缚形成基态的氢原子，求（1）在此过程中放出的光波的波长；（2）电子绕质子运动的动能；（3）电子的德布罗意波长。

　　 附常用物理常数：

• 电子静止质量 $m_0 = 9.1 \times 10^{-31} \\, \mathrm{kg}$
• 电子电量 $e = 1.6 \times 10^{-19} \\, \mathrm{C}$
• 普朗克常数 $h = 6.63 \times 10^{-34} \\, \mathrm{J \cdot s}$
• 真空中光速 $c = 3 \times 10^8 \\, \mathrm{m/s}$
• 玻尔兹曼常数 $k = 1.38 \times 10^{-23} \\, \mathrm{J/K}$
• 普适气体恒量 $R = 8.31 \\, \mathrm{J/(mol \cdot K)}$
• 引力常量 $G = 6.67 \times 10^{-11} \\, \mathrm{N \cdot m^2 / kg^2}$
• 真空电容率 $\varepsilon_0 = 8.85 \times 10^{-12} \\, \mathrm{C^2 / (N \cdot m^2)}$