三门问题

贡献者： Siegfried

1. 问题

　　三门问题，又叫蒙提霍尔问题（Monty Hall problem）其衍生过许多版本，写进过高中数学教科书思考题，在网上讨论也颇多，但目前看到的结论多数不赞同，或者是被限制了条件。下面来看一下这个悖论的原始版本：

　　 Monty Hall 是美国一个电视游戏节目的主持人，你是参赛者。你面对三扇门 A, B, C (或者是 1 号，2 号，3 号)，其中一扇门的后面是汽车，另外两扇门后面是山羊，你的目标是赢得汽车。你随机选择一扇门(假设你选择了 A)，这时主持人打开了 C，C 后面是一只山羊，并给你一次重新选择的机会。现在汽车只可能在 A 和 B 中，你该不该换门，汽车在 A 和 B 后面的概率各是多少？

图 1：选 1 号还是选 2 号？

2. 思考

　　不同的人有不同的思考方式，主要集中在以下几种：

佛性思考法：只剩下两个门了，那么这时候汽车在 A 或 B 后面的概率应该是平等的，换不换无所谓。
反选法：三个门选一个获奖率是 1/3，但如果让你同时选两个门就是 2/3 这是毫无疑问的。你动起小脑筋，心里选了 B+C，嘴上对主持人说选 A，之后不管她从 B 或 C 打开哪一个门(后面是羊)，都相当于为你排除了多数中的错误答案，你间接选择了 B+C，所以换门的概率更大，为 2/3，不换的概率 1/3，这是网上最常见的答案，证明方式各有不同，但事实真如此吗？
经验法：祖先告诉了我们经验的重要性，你在不知是否换门之际，掏出手机 google 了 Monty Hall，发现了她的黑历史，原来，她只在参赛者第一次选对时，才故意打开另一扇门迷惑参赛者。之前所有和你一样参加这个节目的人，凡是第二次换门，最后都空手而归，看到这里后你还坚持换门吗？

3. 为什么会有悖论？

　　除了问题描述本身，还有一个关键之处：Monty Hall 打开另一扇门的动机。这个问题实际是一个缺少先验概率的条件概率问题。不妨我们给它补上：Monty Hall 在你选对的情况下打开另一扇门的概率是 $x$，在你选错的情况下打开另一扇门的概率是 $y$，这道题才能计算正确答案！现在我们来算一算，当 $x$, $y$ 符合什么情况该换门，什么情况不该换。

　　先考虑极端情况：

$x = 1$, $y = 1$: 应该换！参考反选法。
$x = 1$, $y = 0$: 不能换！参考经验法。
$x = 0$, $y = 1$: 请问这个福利节目现在还有么。
$x = 0$, $y = 0$: 会导致不存在打开另一扇门的情况，不合理。

　　根据贝叶斯公式：

\begin{align} \nonumber P(\text{汽车在 A}|\text{打开 C 是羊})&=\frac{P(\text{汽车在 A})P(\text{打开 C 是羊}|\text{汽车在 A})}{P(\text{打开 C 是羊})}\\ \nonumber &=\frac{P(\text{汽车在 A})P(\text{打开 C 是羊}|\text{汽车在 A})}{P(\text{打开 C 是羊}|\text{汽车在 A})P(\text{汽车在 A})+P(\text{打开 C 是羊}|\text{汽车不在 A})P(\text{汽车不在 A})}\\ \nonumber &=\frac{\frac{1}{3}\cdot x\cdot \frac{1}{2}}{\frac{1}{3}\cdot x\cdot \frac{1}{2}+\frac{2}{3}\cdot y\cdot \frac{1}{2}}\\ \nonumber &=\frac{1}{1+\frac{2y}{x}}~. \end{align}

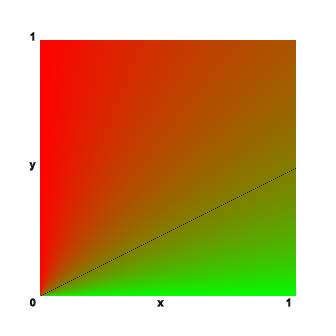
　　可见，不换门赢得汽车的概率，只与 $y$ 与 $x$ 的比例有关，下面是 $x$, $y$ 在[0,1]范围内的热度图像

图 2：$x$ 轴为第一次选对主持人打开另一扇门的概率，$y$ 轴为第一次选错主持人打开另一扇门的概率，绿色表示更容易赢得汽车

　　所以暂时的结论是：

$y/x$ 越小，越靠近绿色，汽车在 A 的概率越接近 1，不应该换；
$y/x$ 越大，越靠近红色，汽车在 A 的概率越接近 0，应该换；
在图中的黑线 $y=0.5x$ 上，换与不换概率均为 0.5

4. Python 验证

　　利用 random（伪）随机数，制造出随机的五组 $x$, $y$ 计算在每次都选 A 门，提供了换门机会，且不换门赢得汽车的理论概率，并模拟汽车真实在 A 门后面几率

import random
random.seed(0)

def monty_hall_problem(max_trial, x, y):
    done = False
    total_car_in_A = 0
    total_trial = 0
    #Monty Hall 问题大量发生，每一次都选A且不换门
    while not done:
        #用1，2，3表示汽车在A，B，C
        car_behind_door = random.randint(1,3)
        if car_behind_door == 1:
            #有x概率开另一扇门，此时不换会赢得汽车
            if random.random() < x:
                total_car_in_A += 1
                total_trial += 1
            #否则不开门，不符合假设
            else:
                continue
        #有y概率开另一扇门，此时不换赢不到
        elif random.random() < y:
            total_trial += 1
        #同样，不符合假设
        else:
            continue
        if total_trial >= max_trial:
            done = True
    return total_car_in_A / total_trial

if __name__ == "__main__":
    for i in range(5):
        #随机选5组随机数
        x = random.random()
        y = random.random()
        #理论值
        p0 = x /(x + 2 * y)
        #实际值
        p = monty_hall_problem(10**6, x, y)
        print("第{0}次随机x = {1:.2%}, y = {2:.2%}，理论概率 x/(x + 2y)：{3:.2%}"
              .format(i+1, x, y, p0))
        print("  百万数量模拟下，汽车在A门后的几率为：{0:.2%}，相对误差为{1:.2%}"
              .format(i+1, p, (p - p0)/ p0))

　　上述代码执行后的结果如下：

第1次随机x = 84.44%, y = 75.80%，理论概率 x/(x + 2y)：35.78%
  百万数量模拟下，汽车在A门后的几率为：35.71%，相对误差为-0.17%
第2次随机x = 76.87%, y = 1.68%，理论概率 x/(x + 2y)：95.82%
  百万数量模拟下，汽车在A门后的几率为：95.82%，相对误差为0.01%
第3次随机x = 35.97%, y = 80.81%，理论概率 x/(x + 2y)：18.20%
  百万数量模拟下，汽车在A门后的几率为：18.17%，相对误差为-0.21%
第4次随机x = 80.72%, y = 63.39%，理论概率 x/(x + 2y)：38.90%
  百万数量模拟下，汽车在A门后的几率为：38.94%，相对误差为0.09%
第5次随机x = 19.08%, y = 86.08%，理论概率 x/(x + 2y)：9.98%
  百万数量模拟下，汽车在A门后的几率为：10.01%，相对误差为0.31%

5. 这就结束了？

　　看到这里，你根据节目历史，估算出了 $x$，$y$，之后通过计算比较了换与不换的概率的大小，去参加节目，是否必有超过一半概率赢回汽车？

　　答案：当然不是！因为这是一个条件概率问题，你不能保证你去参加节目一定会达成条件。很可能你第一次选错直接 GAME OVER 了。

　　既然这样计算上面概率还有什么意义呢？我们已经得出这个结论了不是：如果 Monty Hall 打开另一扇门，给我们一次换门的机会，$x>2y$ 时选择不换，否则选择换。所以，还需一步就可以推导不含条件的全概率公式：

　　 $$ \begin{aligned} &P(\text{赢得汽车})=\\ & \left\{\begin{aligned} &\frac{1}{3}(\overbrace{1-x}^{\text{1-$x$ 概率直接赢}}+\overbrace{x\cdot \frac{x}{x+2y}}^{\text{$x$ 概率开门，乘以不换门赢的概率}})+\frac{2}{3}(\overbrace{y\cdot \frac{x}{x+2y}}^{\text{$y$ 概率开门，乘以不换门赢的概率}}) && \text{ ①}\\ & \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \text{if } x\ge2y \ \ \text{（给机会也不换）}\\ &\frac{1}{3}[1-x+\underbrace{x\cdot(1- \frac{x}{x+2y}}_{\text{这里替换成换门赢的概率，其他同上}})]+\frac{2}{3}[y\cdot(1- \frac{x}{x+2y})]& \text{ ②}\\ & \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \text{if } x<2y \ \ \text{（给机会就换）}~. \end{aligned}\right. \end{aligned} $$

　　化简①式，结果为：1/3, 化简②式，结果为：$(1+2y-x)/3$。

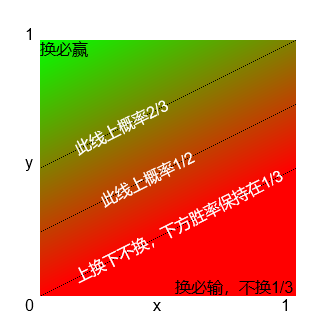
　　下面是全概率下的热度图像

图 3：还是有必要解释一下，这个图片是参加比赛之前根据 $x$，$y$，计算得到最可能赢得汽车的概率；举个例子，$x=0$, $y=0.25$，如果提供了换门机会，那换门胜率将是 100$\%$，因为你若第一次选对主持人根本不会开另一扇门！但你无法在比赛前确定会有换门机会，所以综合胜率是 50$\%$

　　这个结果是符合常理的，仅当 $x=0$，$y=1$ 情况，参赛者必赢（要么第一次选对直接赢得汽车，要么第一次选错 100%开门，第二次换门赢得汽车），其他情况下，根据不同的 $x$, $y$，赢得汽车的概率在 1/3 和 1 之间

6. 结论

　　如果你是参赛者，并且希望赢走汽车，为了提高成功率一定要提前知道 Monty Hall 的策略（根据节目历史估算 $x$, $y$）

　　如果你不知道该不该参加节目，可以通过 汽车价格 × 上面的概率 计算 期望值，如果期望值大于入场门票价格，那么，大量参加节目是稳赚不赔的（当然在 Monty Hall 不会针对你多次参加竞猜而改变策略前提下）。事实上，2005 年 2 月，美国的某一个彩票品种由于设计不周，真的出现过稳赚不赔的情况，被麻省理工一名学生发现并通过反复购买赚到了 300 万美元。链接

　　那么转换思维，如果你是 Monty Hall 呢，你当然不希望参赛者轻松的赢走门后的汽车，应该怎么做？

　　短期做法：

如果对方坚持 “必换” 原则，那么，恭喜你，要么他第一次选错，要么他第二次选错。
如果对方坚持 “不换” 原则，那么也恭喜你，他最多有 1/3 的概率赢得汽车，如果一次选中，试试能不能说动他换一扇门吧。
如果对方相当聪明，或者他看完了这篇文章，并通过统计知道了你的习惯，那么他将很有可能赢得汽车。
如果他的小聪明被你看出，那么针对这一次采取相反策略吧。
如果他也看出了你这一次要用相反策略，那…剩下时间留给脑补。

　　长期做法：

保持 $x\ge 2y$，即参赛者第一次选对下打开另一扇门，提供换门机会的概率，要大于等于选错情况下提供换门机会的 2 倍（保持 2 倍关系即可，相差再大不会影响效果，反而可能会被诟病）。这种情况下任凭参赛者再聪明，也无法奈何，只有 1/3 的概率赢走汽车。

　　本文完，原创文章，作者最早曾发布于个人博客并于 2023 年加入小时百科创作，如需转载，请注明来源。

致读者：小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。因此，我们请求广大读者热心打赏 ，使网站得以健康发展。如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损，并在接下来的一年里向所有读者继续免费提供优质内容。但遗憾的是只有不到 1% 的读者愿意捐款，他们的付出帮助了 99% 的读者免费获取知识，我们在此表示感谢。